The component of a vector r along X-axis will have maximum value if
→r is along +ve x - axis
→r is along +ve y - axis
→r is along -ve y - axis
→r makes an angle of 45∘ with the x-axis
The correct Answer is:A
To solve the problem of finding the condition under which the component of a vector r along the X-axis has a maximum value, we can follow these steps:
1. Understanding Vector Components:
- A vector r can be represented in a coordinate system where it makes an angle θ with the X-axis. The components of the vector can be expressed in terms of its magnitude r and the angle θ.
2. Expression for X-axis Component:
- The component of the vector r along the X-axis is given by the formula:
rx=rcosθ
- Here, rx is the component of the vector along the X-axis, r is the magnitude of the vector, and θ is the angle between the vector and the X-axis.
3. Analyzing the Cosine Function:
- The cosine function cosθ varies between -1 and 1. It reaches its maximum value of 1 when θ=0∘.
- Therefore, to maximize rx, we need to maximize cosθ.
4. Condition for Maximum Component:
- The maximum value of rx occurs when:
cosθ=1atθ=0∘
- This means that the vector r must be aligned along the positive X-axis.
5. Conclusion:
- Thus, the component of the vector r along the X-axis will have its maximum value when the vector is directed along the positive X-axis.
Final Answer:
The component of a vector r along the X-axis will have a maximum value if the vector is along the positive X-axis (i.e., θ=0∘).
---
- A vector r can be represented in a coordinate system where it makes an angle θ with the X-axis. The components of the vector can be expressed in terms of its magnitude r and the angle θ.
- The component of the vector r along the X-axis is given by the formula:
rx=rcosθ
- Here, rx is the component of the vector along the X-axis, r is the magnitude of the vector, and θ is the angle between the vector and the X-axis.
- The cosine function cosθ varies between -1 and 1. It reaches its maximum value of 1 when θ=0∘.
- Therefore, to maximize rx, we need to maximize cosθ.
- The maximum value of rx occurs when:
cosθ=1atθ=0∘
- This means that the vector r must be aligned along the positive X-axis.
- Thus, the component of the vector r along the X-axis will have its maximum value when the vector is directed along the positive X-axis.
The component of a vector r along the X-axis will have a maximum value if the vector is along the positive X-axis (i.e., θ=0∘).
Topper's Solved these Questions
Similar Questions
The component of a vector →A along y-axis will have maximum value if
View SolutionThe component of a vector is
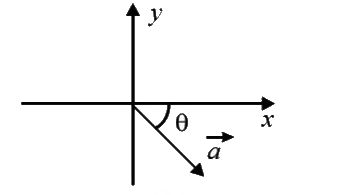
View SolutionWhat is the component of the vector →a along the x-axis in the situation shown in figure ? |→a|=5 units.
View SolutionThe x and Y components of a vector ¯¯¯P have numerical values 5 and 6 respectively. Find the vector ¯¯¯P
View SolutionThe components of a vector →a along and perpendicular to a non-zero vector →b are ________ and ___________, respectively.
View SolutionThe components of a vector along the x- and y- directions are (n+1) and 1, respectively. If the coordinate system is rotated by an angle θ=60∘, then the components change to n and 3. The value of n is
View SolutionFind component of vector A +B along (i) x-axis, (ii) C. Given A=ˆi−2ˆj,B=2ˆi+3ˆk and C=ˆi+ˆj.
View SolutionFind component of vector A +B along (i) x-axis, (ii) C. Given A=ˆi−2ˆj,B=2ˆi+3ˆk and C=ˆi+ˆj.
View SolutionSuppose that →p,→qand→r are three non- coplaner in R3 ,Let the components of a vector→s along →p,→qand→r be 4,3, and 5, respectively , if the components this vector →s along (−→p+→q+→r),(→p−→q+→r)and(−→p−→q+→r) are x, y and z , respectively , then the value of 2x+y+z is
View SolutionThe x and y components of a position vector P have numerical values 5 and 6 respectively. Direction and magnitude of vector P are
View Solution
