Two bodies of masses fall from heights respectively. The ratio of their velocities when the hit the ground is
The correct Answer is:B
To solve the problem of finding the ratio of the velocities of two bodies falling from different heights, we can follow these steps:
1. Understand the Problem: We have two bodies with masses m1 and m2 falling from heights h1 and h2 respectively. We need to find the ratio of their velocities when they hit the ground.
2. Use the Kinematic Equation: The velocity of a body falling from a height can be determined using the equation:
v2=u2+2gh
where v is the final velocity, u is the initial velocity (which is 0 for free fall), g is the acceleration due to gravity, and h is the height.
3. Apply the Equation for Each Body:
- For the first body falling from height h1:
v21=0+2gh1⟹v1=√2gh1
- For the second body falling from height h2:
v22=0+2gh2⟹v2=√2gh2
4. Find the Ratio of Velocities:
- Now, we can find the ratio of the velocities v1 and v2:
v1v2=√2gh1√2gh2=√h1√h2
5. Final Result:
- Therefore, the ratio of their velocities when they hit the ground is:
v1v2=√h1h2
Conclusion:
The ratio of the velocities when the two bodies hit the ground is √h1h2.
v2=u2+2gh
where v is the final velocity, u is the initial velocity (which is 0 for free fall), g is the acceleration due to gravity, and h is the height.
- For the first body falling from height h1:
v21=0+2gh1⟹v1=√2gh1
- For the second body falling from height h2:
v22=0+2gh2⟹v2=√2gh2
- Now, we can find the ratio of the velocities v1 and v2:
v1v2=√2gh1√2gh2=√h1√h2
- Therefore, the ratio of their velocities when they hit the ground is:
v1v2=√h1h2
The ratio of the velocities when the two bodies hit the ground is √h1h2.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE & PLANE BOOK - VMC MODULES ENGLISHCHAPTER - MOTION IN A STRAIGHT LINE & PLANE EXERCISE - ENABLE
50 Videos
- MOTION IN A STRAIGHT LINE & PLANE BOOK - VMC MODULES ENGLISHCHAPTER - MOTION IN A STRAIGHT LINE & PLANE EXERCISE - EFFICIENT
50 Videos
- MOCK TEST 9BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 9EXERCISE - PHYSICS (SECTION 2)
5 Videos
- Motion in Straight Line BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - IN-CHAPTER EXERCISE-J
10 Videos
Similar Questions
Two bodies of masses (m1) and (m2) are droppded from heithts h1 and h2, respectively. They reach the ground after time t1 and t2 and strike the ground with v1 and v2, respectively Choose the correct relations from the following.
View SolutionTwo spherical bodies of mass m1 & m2 are having radius 1 m & 2 m respectively. The gravitational field of the two bodies with their radial distance is shown below. The value of m1m2 is
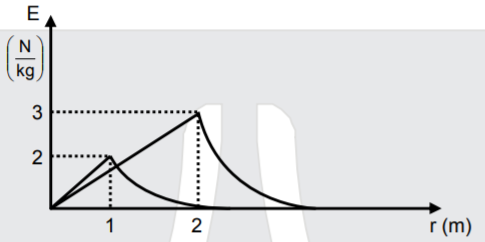 -
-
View SolutionA body of mass m falls from a height h1 and rises to a height h2. The magnitude of the change in momentum during the impact with the ground.
View SolutionTwo stones are falling at a place from heights in the ratio 2:3. Their velocities on reaching the ground are in the ratio
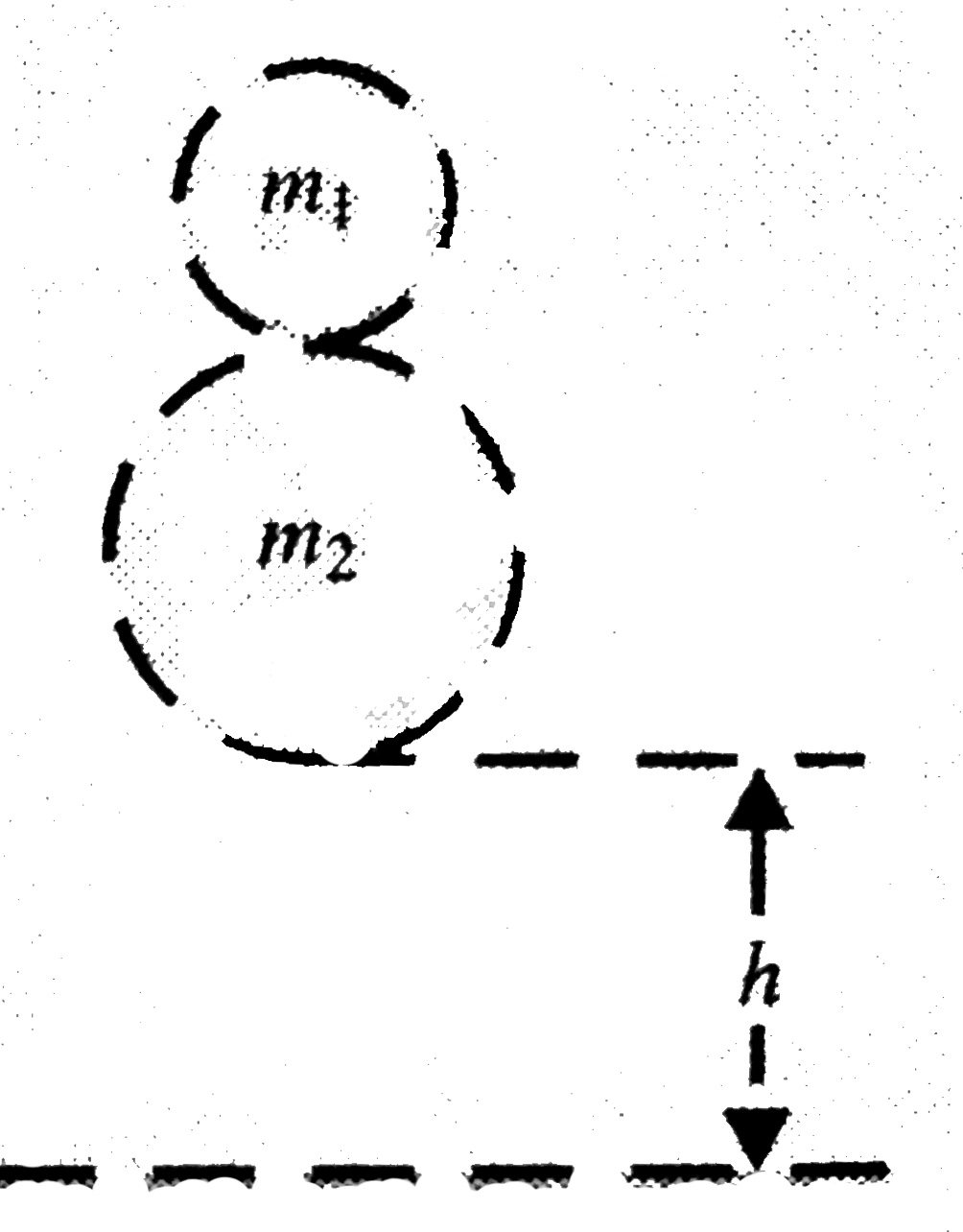
View SolutionTwo spherical bodies of mass m1 and m2 fall freely through a distance h. before the body m2 collides with the ground. If the coefficient of restitution of all collisions is e, find the velocity of m1 just after it collides with m2
View SolutionA solid sphere and a solid cylinder of same mass are rolled down on two inclined planes of heights h1 and h2 respectively. If at the bottom of the plane the two objects have same linear velocities, then the ratio of h1:h2 is
View SolutionTwo bodies of mass 2 kg and 5 kg have position (1 m, 2 m, 1 m) and (3 m, 2 m, -1 m) respectively. The position vector of centre of mass is
View SolutionTwo masses m1 and m2(m1>m2) are falling from the same height when same air resistance acts on them
View SolutionAssertion : Two bodies of unequal masses m1andm2 are dropped from the same height. If the resistance offered by air to the motion of both bodies is the same, the bodies will reach the earth at the same time.
Reason : For equal air resistance, acceleration of fall of masses m1andm2 will be different.
View SolutionTwo bodies of masses M and m are allowed to fall from the same height. It the resistance for each be the same, then, will both the bodies reach the earth simultaneously ?
View Solution
