From a ballon rising vertically upwards at 5 m/s, a stone is thrown up at 10 m/s relative to the balloon. Its velocity with respect to ground after 2 sec is - (assume g = 10 m/s2)
zero
5ms−1
10ms−1
20ms−1
The correct Answer is:B
To solve the problem step by step, we will break down the motion of the stone thrown from the balloon and calculate its velocity with respect to the ground after 2 seconds.
Step 1: Identify the initial velocities
The balloon is rising vertically upwards at a speed of 5 m/s. The stone is thrown upwards at a speed of 10 m/s relative to the balloon.
Initial velocity of the stone with respect to the ground (u):
- Velocity of the balloon (upwards) = 5 m/s
- Velocity of the stone relative to the balloon (upwards) = 10 m/s
Thus, the initial velocity of the stone with respect to the ground is:
u=Velocity of balloon+Velocity of stone relative to balloon
u=5m/s+10m/s=15m/s
Step 2: Calculate the final velocity after 2 seconds
To find the final velocity of the stone after 2 seconds, we will use the equation of motion:
v=u−g⋅t
Where:
- v = final velocity
- u = initial velocity (15 m/s)
- g = acceleration due to gravity (10 m/s²)
- t = time (2 seconds)
Substituting the values into the equation:
v=15m/s−(10m/s2⋅2s)
v=15m/s−20m/s
v=−5m/s
Conclusion
The velocity of the stone with respect to the ground after 2 seconds is −5m/s.
---
The balloon is rising vertically upwards at a speed of 5 m/s. The stone is thrown upwards at a speed of 10 m/s relative to the balloon.
- Velocity of the balloon (upwards) = 5 m/s
- Velocity of the stone relative to the balloon (upwards) = 10 m/s
u=Velocity of balloon+Velocity of stone relative to balloon
u=5m/s+10m/s=15m/s
To find the final velocity of the stone after 2 seconds, we will use the equation of motion:
v=u−g⋅t
Where:
- v = final velocity
- u = initial velocity (15 m/s)
- g = acceleration due to gravity (10 m/s²)
- t = time (2 seconds)
v=15m/s−(10m/s2⋅2s)
v=15m/s−20m/s
v=−5m/s
The velocity of the stone with respect to the ground after 2 seconds is −5m/s.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE & PLANE BOOK - VMC MODULES ENGLISHCHAPTER - MOTION IN A STRAIGHT LINE & PLANE EXERCISE - EFFICIENT
50 Videos
- MOCK TEST 9BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 9EXERCISE - PHYSICS (SECTION 2)
5 Videos
- Motion in Straight Line BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - IN-CHAPTER EXERCISE-J
10 Videos
Similar Questions
A ball is thrown vertically upward attains a maximum height of 45 m. The time after which velocity of the ball become equal to half the velocity of projection ? (use g = 10 m/s2)
View SolutionA man in a balloon, rising vertically with an acceleration of 5m/s2, releases a ball 10 s after the balloon is let go from the ground. The greatest height above the ground reached by the ball is
View SolutionFrom the top of a tower, a particle is thrown vertically downwards with a velocity of 10m/s. The ratio of the distances, covered by it in the 3rd and 2nd seconds of the motion is (Takeg=10m/s2).
View SolutionA ballon moves up with a velocity 5m/s. A stone is thrown from it with a horizontal velocity 2m/s relative to it. The stone hits the ground at a point 10m horizontally away from it. (Take g=10m/s2)
View SolutionA stone is thrown vertically up at 20 m/s from a tower 80 m height. The speed with which it hits the ground is [g=10m/s2]
View SolutionA balloon is going upwards with a constant velocity 15m/s. When the ballooon is at 50 m height, a stone is dropped outside from the balloon. How long will stone take to reach at the ground? (take g=10m/s2)
View SolutionA stone is thrown upwards and it rises to a height 0f 200m. The relative velocity of the stone with respect to the earth will be maximum at :-
View SolutionA ball is throw vertically upward. It has a speed of 10m/s when it has reached on half of its maximum height. How high does the ball rise ? (Taking g=10m/s2).
View SolutionA balloon is moving along with constant upward acceleration of 1m/s2. A stone is thrown from the balloon downwards with speed 10m/s with respect to the balloon. At the time of projectile balloon is at height 120m from the ground and is moving with speed 20m/s. Find the time required to fall on the ground by the stone after the projection.
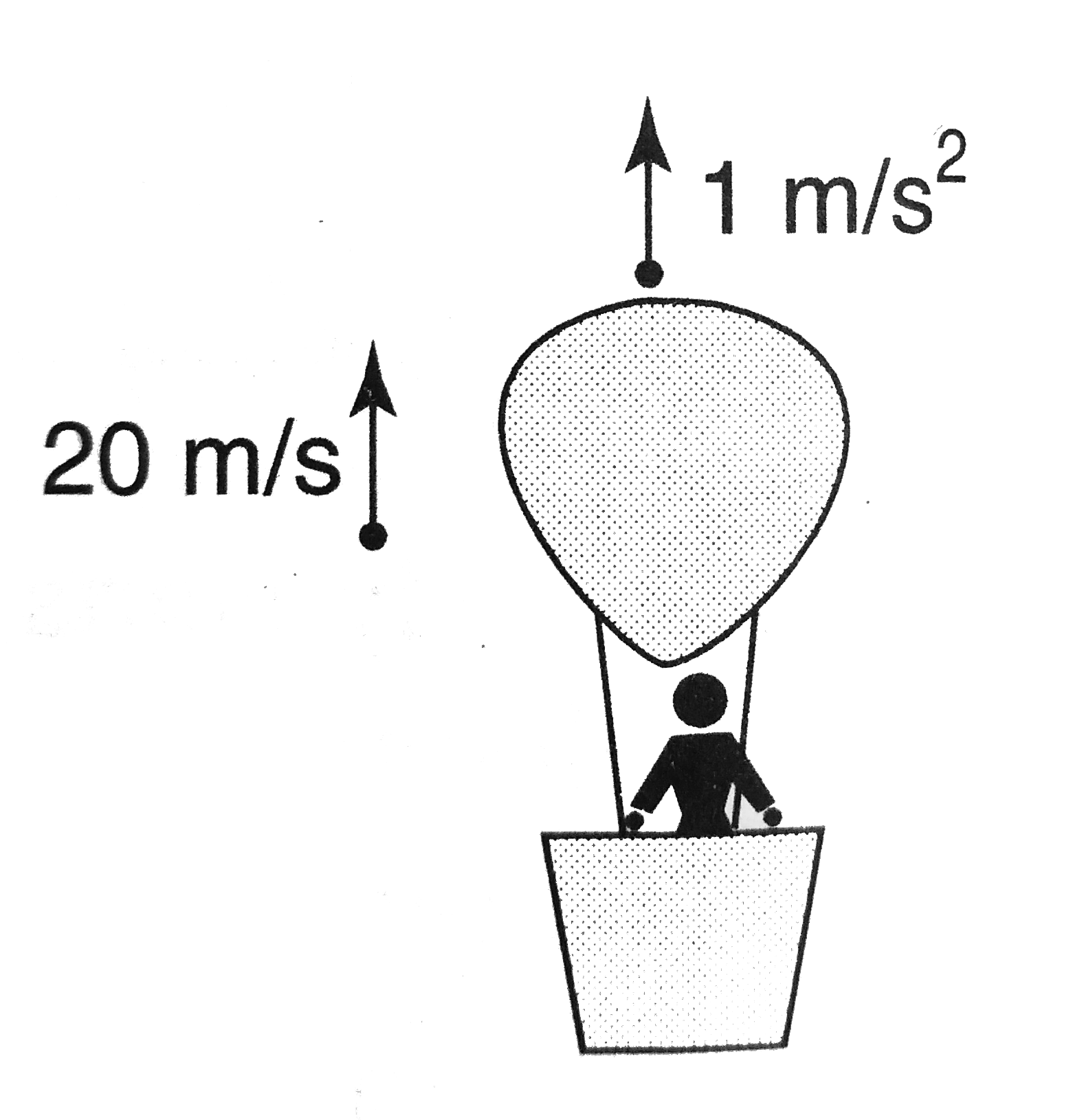
View SolutionA ball is thrown vertically upwards. It returns 6 s later. Calculate the initial velocity of the ball. (Take g=10m s−2 )
View Solution