A ballon moves up with a velocity 5m/s. A stone is thrown from it with a horizontal velocity 2m/s relative to it. The stone hits the ground at a point 10m horizontally away from it. (Take g=10m/s2)
the time of flight of the stone is 5 seconds
height of the ballon at the time of throwing the stone is 100m.
the speed with it will hit the ground is 40m/s
the time of flight of the stone will increase if the horizontal velocity of the stone is incresed.
The correct Answer is:A, B
To solve the problem step by step, we will analyze the motion of the balloon and the stone separately, and then combine the results to find the required quantities.
Step 1: Understand the Motion of the Balloon
The balloon is moving upwards with a velocity of 5m/s. This means that at the moment the stone is thrown, the balloon has a vertical velocity of 5m/s.
Step 2: Analyze the Horizontal Motion of the Stone
The stone is thrown horizontally with a velocity of 2m/s relative to the balloon. Since the balloon is moving upwards, the horizontal velocity of the stone with respect to the ground will be the same, 2m/s.
Step 3: Determine the Time of Flight
The stone hits the ground at a point 10m horizontally away from the point where it was thrown. We can use the horizontal motion to find the time of flight t:
Horizontal distance=Horizontal velocity×Time
Given that the horizontal distance is 10m and the horizontal velocity is 2m/s:
10=2×t
Solving for t:
t=102=5s
Step 4: Calculate the Height from Which the Stone is Thrown
Now we need to find the height h from which the stone is thrown. We can use the vertical motion equation:
h=ut+12gt2
Where:
- u=5m/s (initial vertical velocity of the stone)
- g=10m/s2 (acceleration due to gravity)
- t=5s
Substituting the values:
h=5×5+12×10×(5)2
Calculating:
h=25+12×10×25
h=25+125=150m
Step 5: Calculate the Final Velocity of the Stone Just Before Hitting the Ground
The final vertical velocity v of the stone just before it hits the ground can be calculated using:
v=u+gt
Where:
- u=5m/s (initial vertical velocity)
- g=10m/s2
- t=5s
Substituting the values:
v=5+10×5
v=5+50=55m/s
Step 6: Calculate the Resultant Velocity of the Stone
The resultant velocity of the stone just before it hits the ground can be found using the Pythagorean theorem, since the stone has both horizontal and vertical components of velocity:
vresultant=√(vx)2+(vy)2
Where:
- vx=2m/s (horizontal velocity)
- vy=55m/s (vertical velocity)
Calculating:
vresultant=√(2)2+(55)2
vresultant=√4+3025=√3029≈55m/s
Final Answer
The height from which the stone was thrown is 150m and the resultant velocity just before hitting the ground is approximately 55m/s.
---
The balloon is moving upwards with a velocity of 5m/s. This means that at the moment the stone is thrown, the balloon has a vertical velocity of 5m/s.
The stone is thrown horizontally with a velocity of 2m/s relative to the balloon. Since the balloon is moving upwards, the horizontal velocity of the stone with respect to the ground will be the same, 2m/s.
The stone hits the ground at a point 10m horizontally away from the point where it was thrown. We can use the horizontal motion to find the time of flight t:
Now we need to find the height h from which the stone is thrown. We can use the vertical motion equation:
- u=5m/s (initial vertical velocity of the stone)
- g=10m/s2 (acceleration due to gravity)
- t=5s
h=25+125=150m
The final vertical velocity v of the stone just before it hits the ground can be calculated using:
- u=5m/s (initial vertical velocity)
- g=10m/s2
- t=5s
v=5+50=55m/s
The resultant velocity of the stone just before it hits the ground can be found using the Pythagorean theorem, since the stone has both horizontal and vertical components of velocity:
- vx=2m/s (horizontal velocity)
- vy=55m/s (vertical velocity)
vresultant=√4+3025=√3029≈55m/s
The height from which the stone was thrown is 150m and the resultant velocity just before hitting the ground is approximately 55m/s.
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PHYSICS
784 Videos
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS SEC - 2
20 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
Similar Questions
A balloon moves up vertically such that if a stone is thrown from it with a horizontal velocity v0 relative to it the stone always hits the ground at a fixed point 2v20/g horizontally away from it. Find the height of the balloon as a function of time.
View SolutionA stone is thrown vertically up at 20 m/s from a tower 80 m height. The speed with which it hits the ground is [g=10m/s2]
View Solution
Knowledge Check
A stone is thrown horizontally with velocity u. The velocity of the stone 0.5 s later is 3u/2. The value of u is
A2.2ms−1B3.3ms−1C4.4ms−1D1.1ms−1A body is thrown with a velocity of 9.8 m/s making an angle of 30∘ with the horizontal. It will hit the ground after a time
A3 sB2sC1.5 sD1 s
A projectile is thrown with a velocity of 20 m/s, at an angle of 60∘ with the horizontal. After how much time the velocity vector will make an angle of 45∘ with the horizontal (in upward direction) is (take g=10m/s2)−
View SolutionA ball is thrown from the top of a tower with an intial velocity of 10 m//s at an angle 37∘ above the horizontal, hits the ground at a distance 16 m from the base of tower. Calculate height of tower. [g=10m/s2]
View SolutionA body is prodected with initial velocity(5ˆi+12ˆi) m//s from origin . Gravity acts in negative y direction. The horizontal rang is (Take g = 10 m/s2)
View SolutionA balloon is moving upwards with velocity 10m/s. It releases a stone which comes down to the ground in 11s. The height of the balloon from the ground at the moment when the stone was dropped is (g=10m/s2)
View SolutionA ball is thrown from the top of 36m high tower with velocity 5m/ss at an angle 37∘ above the horizontal as shown. Its horizontal distance on the ground is closest to [g=10m/s2
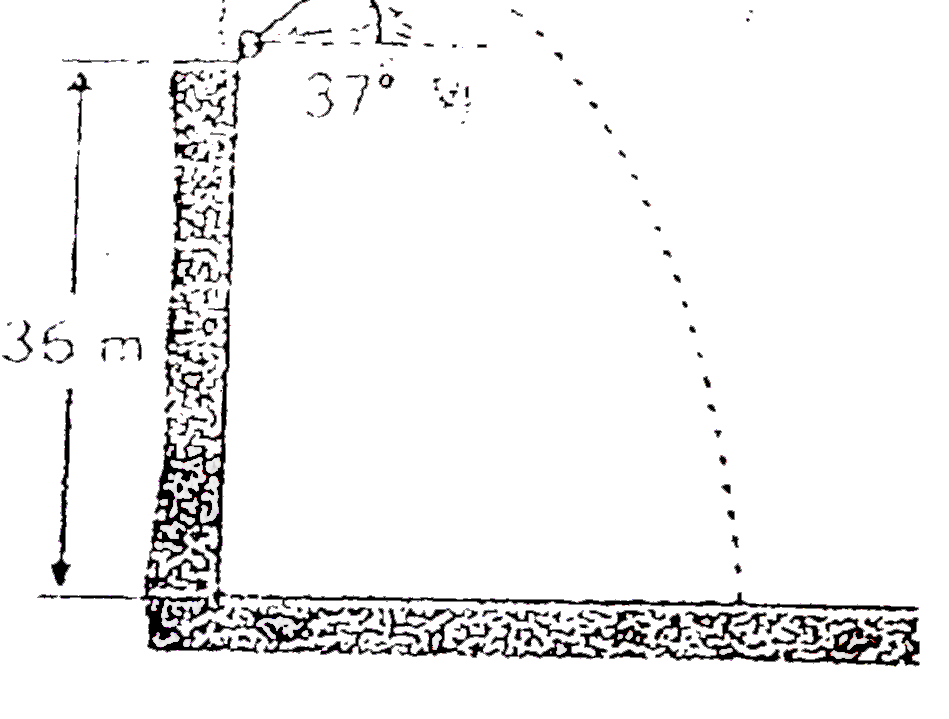 :
:
View SolutionA ball is thrown upward with speed 10 m/s from the top to the tower reaches the ground with a speed 20 m/s. The height of the tower is [Take g=10m/s2]
View Solution
