Given that C denotes capacitance of a capacitor and V is the potential difference across its plates. Then the dimensions of CV2 are same as that of
momentum
power
forces
torque
The correct Answer is:D
To solve the problem, we need to determine the dimensions of the expression CV2 where C is the capacitance and V is the potential difference across the plates of a capacitor.
1. Identify the dimensions of capacitance C:
The capacitance C is defined as the charge Q per unit potential difference V:
C=QV
The dimension of charge Q is (I)(T) (where I is current and T is time). The potential difference V has the dimension of energy per unit charge, which can be expressed as:
V=EQ
The dimension of energy E is (M)(L2)(T−2). Therefore, the dimension of V is:
(V)=(M)(L2)(T−2)(I)(T)=(M)(L2)(T−3)(I−1)
2. Substituting the dimensions into the capacitance equation:
Now substituting the dimensions of Q and V into the capacitance equation:
(C)=(I)(T)(M)(L2)(T−3)(I−1)=(I2)(T4)(M)(L2)
3. Calculate the dimensions of CV2:
Now we need to calculate the dimensions of CV2:
CV2=C⋅V⋅V
The dimension of V2 is:
(V2)=((M)(L2)(T−3)(I−1))2=(M2)(L4)(T−6)(I−2)
Therefore, the dimensions of CV2 are:
(CV2)=(C)⋅(V2)=((I2)(T4)(M)(L2))⋅((M2)(L4)(T−6)(I−2))
Simplifying this:
(CV2)=(I2)(T4)(M2)(L4)(T−6)(I−2)(M)(L2)=(M)(L2)(T−2)
4. Conclusion:
The dimensions of CV2 are the same as the dimensions of energy, which is (M)(L2)(T−2).
Final Answer:
The dimensions of CV2 are the same as that of energy.
---
The capacitance C is defined as the charge Q per unit potential difference V:
C=QV
The dimension of charge Q is (I)(T) (where I is current and T is time). The potential difference V has the dimension of energy per unit charge, which can be expressed as:
V=EQ
The dimension of energy E is (M)(L2)(T−2). Therefore, the dimension of V is:
(V)=(M)(L2)(T−2)(I)(T)=(M)(L2)(T−3)(I−1)
Now substituting the dimensions of Q and V into the capacitance equation:
(C)=(I)(T)(M)(L2)(T−3)(I−1)=(I2)(T4)(M)(L2)
Now we need to calculate the dimensions of CV2:
CV2=C⋅V⋅V
The dimension of V2 is:
(V2)=((M)(L2)(T−3)(I−1))2=(M2)(L4)(T−6)(I−2)
Therefore, the dimensions of CV2 are:
(CV2)=(C)⋅(V2)=((I2)(T4)(M)(L2))⋅((M2)(L4)(T−6)(I−2))
Simplifying this:
(CV2)=(I2)(T4)(M2)(L4)(T−6)(I−2)(M)(L2)=(M)(L2)(T−2)
The dimensions of CV2 are the same as the dimensions of energy, which is (M)(L2)(T−2).
The dimensions of CV2 are the same as that of energy.
Topper's Solved these Questions
- UNITS, MEASUREMENTS & ERRORSBOOK - VMC MODULES ENGLISHCHAPTER - UNITS, MEASUREMENTS & ERRORSEXERCISE - Efficient
50 Videos
- UNITS, MEASUREMENTS & ERRORSBOOK - VMC MODULES ENGLISHCHAPTER - UNITS, MEASUREMENTS & ERRORSEXERCISE - Impeccable
51 Videos
- UNITS, MEASUREMENTS & ERRORSBOOK - VMC MODULES ENGLISHCHAPTER - UNITS, MEASUREMENTS & ERRORSEXERCISE - IN - CHAPTER EXERCISE - B
10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - IMPECCABLE
56 Videos
- WAVE MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE ADVANCED ARCHIVE LEVEL 2 (TRUE FALSE TYPE)
4 Videos
Similar Questions
The displacement current flows in the dielectric of a capacitor when the potential difference across its plates-
View SolutionThe displacement current flows in the dielectric of a capacitor when the potential difference across its plates-
View SolutionIf L,R,C,andV, respectively , represent inductance , resistance , capacitance and potential difference , then the dimensions of L/RCV are the same as those of
View Solutiongiven that potential differene across 1μF capacitor is 10V. Then,
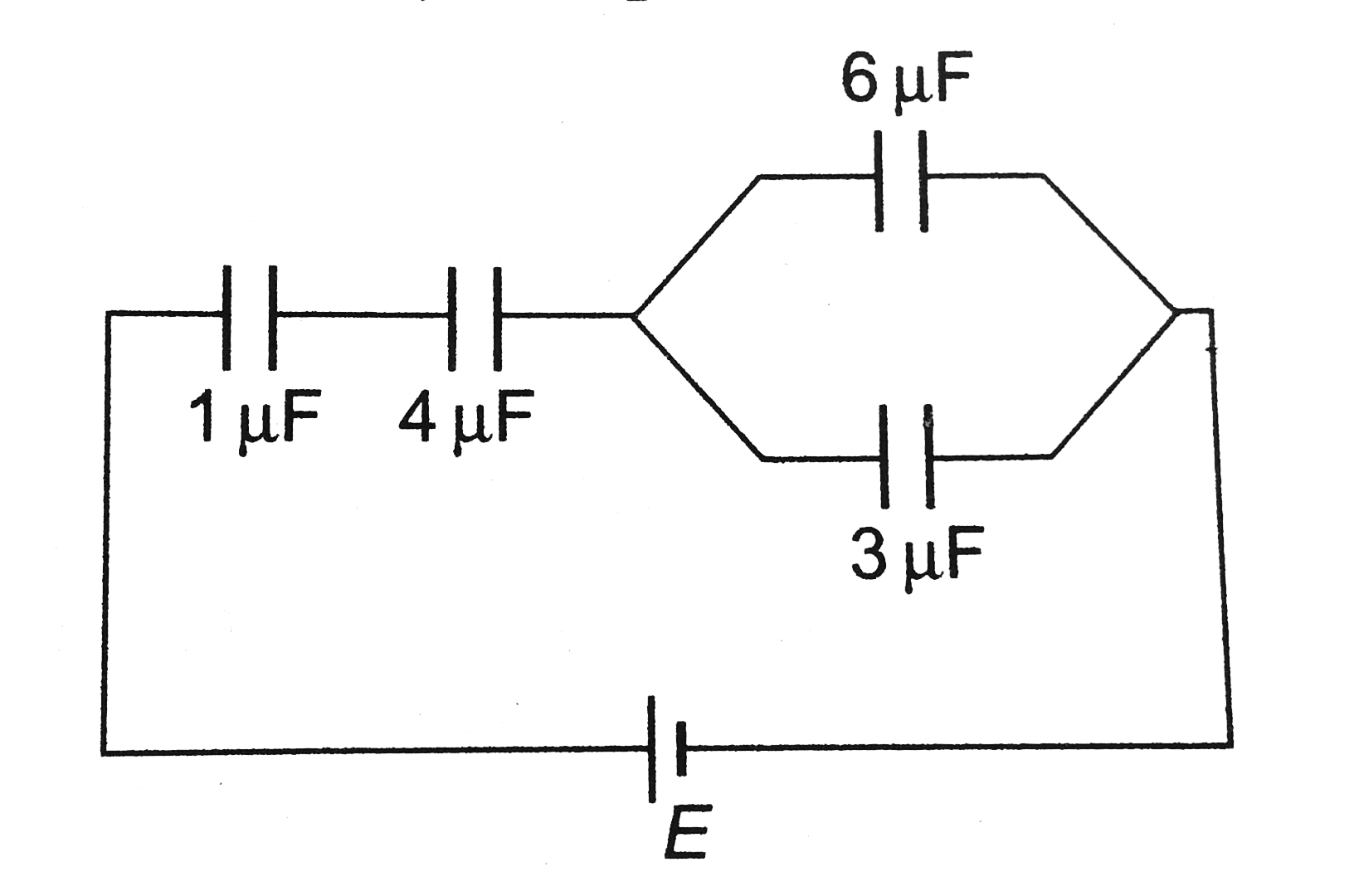
View SolutionIf C be the capacitance and V be the electric potential, then the dimensional formula of CV2 is
View SolutionThree capacitors each of capacitance 9 pF are connected in series. What is the total capacitance of the combination ?
View SolutionIn the given circuit, with steady current, the potential difference across the capacitor is
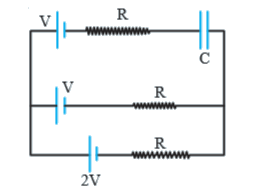
View SolutionA capacitor of capacitance C is charged to a potential difference V0. The charged battery is disconnected and the capacitor is connected to a capacitor of unknown capacitance Cx. The potential difference across the combination is V. The value of Cx should be
View SolutionAn AC source is connected with a resistance ( R) and an unchanged capacitance C, in series. The potential difference across the resistor is in phase with the initial potential difference across the capacitor for the first time at the instant (assume that at t =0 , emf is zero)
View SolutionIn the given circuit, the potential difference across the 6μF capacitor in steady state is
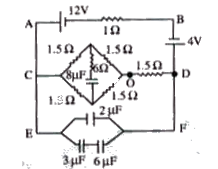
View Solution
