The displacement current flows in the dielectric of a capacitor when the potential difference across its plates-
is increasing with time
is decreasing with time
has assumed a constant value
becomes zero
The correct Answer is:A, B
To solve the question regarding the displacement current in the dielectric of a capacitor when the potential difference across its plates is changing, we can follow these steps:
Step 1: Understand the Concept of Displacement Current
Displacement current is a term introduced by James Clerk Maxwell to account for the changing electric field in the dielectric of a capacitor when there is a time-varying electric field. It is given by the equation:
Id=ϵ0dEdtA
where Id is the displacement current, ϵ0 is the permittivity of free space, E is the electric field, and A is the area of the plates.
Step 2: Analyze the Charging of a Capacitor
When a capacitor is charged, the voltage across its plates increases. This change in voltage leads to a change in the electric field E in the dielectric between the plates. As the electric field changes, the displacement current Id also changes.
Step 3: Determine the Behavior of the Potential Difference
1. Increasing Potential Difference: When the capacitor is charging, the potential difference across its plates is increasing.
2. Decreasing Potential Difference: If the capacitor is discharging, the potential difference is decreasing.
3. Constant Potential Difference: This would imply that there is no change in the electric field, hence no displacement current.
4. Zero Potential Difference: This means the capacitor is fully discharged, and there would be no displacement current.
Step 4: Conclusion Based on the Options
Given the options:
- (a) Increasing with time
- (b) Decreasing with time
- (c) Assumes a constant value
- (d) Becomes 0
When the potential difference across the plates of the capacitor is increasing (during charging), the displacement current is also present and increasing. However, if we consider the scenario where the capacitor is discharging, the potential difference decreases, and so does the displacement current.
Final Answer
The displacement current flows in the dielectric of a capacitor when the potential difference across its plates is decreasing with time. Thus, the correct option is (b).
---
Displacement current is a term introduced by James Clerk Maxwell to account for the changing electric field in the dielectric of a capacitor when there is a time-varying electric field. It is given by the equation:
Id=ϵ0dEdtA
where Id is the displacement current, ϵ0 is the permittivity of free space, E is the electric field, and A is the area of the plates.
When a capacitor is charged, the voltage across its plates increases. This change in voltage leads to a change in the electric field E in the dielectric between the plates. As the electric field changes, the displacement current Id also changes.
1. Increasing Potential Difference: When the capacitor is charging, the potential difference across its plates is increasing.
2. Decreasing Potential Difference: If the capacitor is discharging, the potential difference is decreasing.
3. Constant Potential Difference: This would imply that there is no change in the electric field, hence no displacement current.
4. Zero Potential Difference: This means the capacitor is fully discharged, and there would be no displacement current.
Given the options:
- (a) Increasing with time
- (b) Decreasing with time
- (c) Assumes a constant value
- (d) Becomes 0
The displacement current flows in the dielectric of a capacitor when the potential difference across its plates is decreasing with time. Thus, the correct option is (b).
Topper's Solved these Questions
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 2
6 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP.No.71
1 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems
31 Videos
Similar Questions
Find charge on each capacitor and potential difference across each capacitor .

View SolutionTwo identical parallel plate capacitors are connected in series and then joined in series with a battery of 100V. A slab of dielectric constant K=3 is inserted between the plates of the first capacitor. Then, the potential difference across the capacitor will be, respectively.
View Solution
Knowledge Check
When a current of 2 A flows in a battery from negative to positive terminal, the potential difference across it is 12 V. If a current of 3 A flowing in the opposite direction produces a potential difference of 15 V, the emf of the battery is
A12.6VB13.2VC13.5VD14.0V
Given that C denotes capacitance of a capacitor and V is the potential difference across its plates. Then the dimensions of CV2 are same as that of
View SolutionA capacitor of capacity 2μF is changed to a potential different of 12V . It is then connected across an inductor of inductance 0.6mH What is the current in the circuit at a time when the potential difference across the capacitor is 6.0V ?
View SolutionA capacitor of capacity 2μF is changed to a potential different of 12V . It is then connected across an inductor of inductance 0.6mH What is the current in the circuit at a time when the potential difference across the capacitor is 6.0V ?
View SolutionIn the given circuit, with steady current, the potential difference across the capacitor is
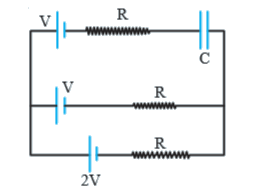
View SolutionAlternating current flowing through a certain electrical device leads over the potential difference across it by 90∘. State whether this device is a resistor, capacitor or an inductor.
View SolutionAssertion : When a dielectric is placed in an electric field, the electric field with in the dielectric as well as. Potential difference across the capacitor plates are reduced by a factor K (battery is not connected).
Reason : The dielectric constant is the ratio of the absolute permittivity of the dielectric to the to the permittivity of the free space.
View SolutionA : The displacement current goes through the gap between the plates of a capacitor when the charge on the capacitor does not change.
R : Displacement current arises only when the electric field is constant.
View Solution
