A body A mass m1 exerts a force on another body B of mass m2 . If the acceleration of B be a2 , then the acceleration (in magnitude) of A is
Zero
m2a2m1
m1a2m2
a2
The correct Answer is:B
To solve the problem, we need to analyze the forces acting on the two bodies, A and B, and apply Newton's laws of motion. Let's break it down step by step.
Step 1: Understand the scenario
We have two bodies:
- Body A with mass m1
- Body B with mass m2
Body A exerts a force on Body B, causing Body B to accelerate with an acceleration a2.
Step 2: Apply Newton's Third Law
According to Newton's Third Law of Motion, for every action, there is an equal and opposite reaction. This means that the force exerted by Body A on Body B is equal in magnitude and opposite in direction to the force exerted by Body B on Body A.
Step 3: Write the equations for forces
The force exerted by Body A on Body B can be expressed using Newton's second law:
FAB=m2⋅a2
where FAB is the force exerted by A on B.
By Newton's Third Law, the force exerted by Body B on Body A is:
FBA=m1⋅a1
where a1 is the acceleration of Body A.
Step 4: Set the forces equal
Since FAB=FBA, we can set the two expressions equal:
m2⋅a2=m1⋅a1
Step 5: Solve for the acceleration of Body A
To find the acceleration of Body A (a1), we can rearrange the equation:
a1=m2⋅a2m1
Conclusion
Thus, the magnitude of the acceleration of Body A is given by:
a1=m2⋅a2m1
Final Answer
The acceleration of Body A in magnitude is m2⋅a2m1.
---
We have two bodies:
- Body A with mass m1
- Body B with mass m2
According to Newton's Third Law of Motion, for every action, there is an equal and opposite reaction. This means that the force exerted by Body A on Body B is equal in magnitude and opposite in direction to the force exerted by Body B on Body A.
The force exerted by Body A on Body B can be expressed using Newton's second law:
FAB=m2⋅a2
where FAB is the force exerted by A on B.
FBA=m1⋅a1
where a1 is the acceleration of Body A.
Since FAB=FBA, we can set the two expressions equal:
m2⋅a2=m1⋅a1
To find the acceleration of Body A (a1), we can rearrange the equation:
a1=m2⋅a2m1
Thus, the magnitude of the acceleration of Body A is given by:
a1=m2⋅a2m1
The acceleration of Body A in magnitude is m2⋅a2m1.
Topper's Solved these Questions
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - EFFICIENT
50 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE Advanced (archive)
14 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)
55 Videos
Similar Questions
A force produces an acceleration of 4ms−2 in a body of mass m1 and the same force produces an acceleration of 6ms−2 in another body oa mass m2. If the same force is applied to (m1+m2), then the acceleration will be
View SolutionTwo bodies of masses 4 kg and 5kg are acted upon by the same force. If the acceleration of lighter body is 2m/sec2, then the acceleration of the heavier body is:-
View SolutionA body of mass m1 collides elastically with another body of mass m2 at rest. If the velocity of m1 after collision is 23 times its initial velocity, the ratio of their masses is :
View SolutionA constant force of 5 N can produce an acceleration of 1 m/s2 on the body of mass m1 and 2m/s2 on the body of mass m2 . If both the masses are tied together and same force is applied then what will be the acceleration of the system ?
View SolutionFigure shows a block of mass m1 sliding on a block of mass m2, with m1>m2. Find the

(a) acceleration of each block
(b) tension in the string
(c ) force exerted by m1 on m2. ltbr> (d) force exerted by m2 on the incline.
View SolutionFind the friction force due to air on a body of mass 1 kg falling with acceleration 8m/s2 :-
View SolutionDue to the application of a force on a body of mass 100 kg that is initially at rest, the body moves with an acceleration of 20ms−2 in the direction of the force. Find the magnitude of the force.
View SolutionIn the figure shown, the acceleration of block of mass m2 is 2m/s2. The acceleration of m1 :
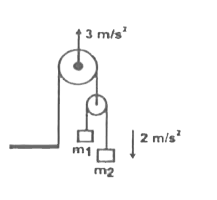
View SolutionA force of10N gives a mass m1,an acceleration of 2ms−2 and a mass m2,an acceleration of 3ms−2.What acceleration would it give in ms2 if both the masses were tied together?
View SolutionA force of 5N gives a mass m1, an acceleration of 10m/s2, and a mass m2, an acceleration of 20m/s2. What acceleration would it give if both the masses were tied together?
View Solution
