An object of mass 'm' is attached to a vertical fixed spring of spring constant 'k' and is allowed to fall under the gravity. What is the distance traversed by the object before being stopped ?
mg/k
2mg/k
mg/2k
none of these
The correct Answer is:B
To solve the problem of an object of mass 'm' attached to a vertical fixed spring of spring constant 'k' falling under gravity, we will use the principle of conservation of energy. Here's the step-by-step solution:
Step 1: Understand the Initial and Final Conditions
- Initially, the mass 'm' is at rest at a certain height above the spring.
- When the mass is allowed to fall, it stretches the spring until it comes to a stop momentarily at the maximum stretch distance 'x'.
Step 2: Identify the Energies Involved
- Potential Energy due to Gravity (PE_gravity): When the mass falls a distance 'x', the potential energy is given by:
PEgravity=m⋅g⋅x
- Elastic Potential Energy in the Spring (PE_spring): The energy stored in the spring when it is stretched by a distance 'x' is:
PEspring=12kx2
Step 3: Apply Conservation of Energy
- At the point of maximum stretch, the total mechanical energy is conserved. Thus, the potential energy due to gravity will be equal to the elastic potential energy in the spring:
m⋅g⋅x=12kx2
Step 4: Rearrange the Equation
- Rearranging the equation gives:
12kx2−m⋅g⋅x=0
- This can be factored as:
x(12kx−m⋅g)=0
Step 5: Solve for 'x'
- The solutions to this equation are:
1. x=0 (the trivial solution, where the mass does not fall)
2. 12kx−m⋅g=0
Solving for 'x':
12kx=m⋅g
kx=2m⋅g
x=2m⋅gk
Step 6: Final Result
- The distance traversed by the object before being stopped is:
x=2mgk
- Initially, the mass 'm' is at rest at a certain height above the spring.
- When the mass is allowed to fall, it stretches the spring until it comes to a stop momentarily at the maximum stretch distance 'x'.
- Potential Energy due to Gravity (PE_gravity): When the mass falls a distance 'x', the potential energy is given by:
PEgravity=m⋅g⋅x
- Elastic Potential Energy in the Spring (PE_spring): The energy stored in the spring when it is stretched by a distance 'x' is:
PEspring=12kx2
- At the point of maximum stretch, the total mechanical energy is conserved. Thus, the potential energy due to gravity will be equal to the elastic potential energy in the spring:
m⋅g⋅x=12kx2
- Rearranging the equation gives:
12kx2−m⋅g⋅x=0
- This can be factored as:
x(12kx−m⋅g)=0
- The solutions to this equation are:
1. x=0 (the trivial solution, where the mass does not fall)
2. 12kx−m⋅g=0
Solving for 'x':
12kx=m⋅g
kx=2m⋅g
x=2m⋅gk
- The distance traversed by the object before being stopped is:
x=2mgk
Topper's Solved these Questions
- WORK ENERGY AND POWER BOOK - VMC MODULES ENGLISHCHAPTER - WORK ENERGY AND POWER EXERCISE - IMPECCABLE
54 Videos
- WORK ENERGY AND POWER BOOK - VMC MODULES ENGLISHCHAPTER - WORK ENERGY AND POWER EXERCISE - ENABLE
50 Videos
- WAVE MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE ADVANCED ARCHIVE LEVEL 2 (TRUE FALSE TYPE)
4 Videos
Similar Questions
A block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionWhen a particle of mass m is attached to a vertical spring of spring constant k and released, its motion is described by y(t)=y0sin2ωt, where 'y' is measured from the lower end of unstretched spring. Then ω is :
View Solution
Knowledge Check
A particle of mass m is hanging vertically by an ideal spring of force constant K . If the mass is made to oscillate vertically, its total energy is
Amaximum at the extreme positionBmaximum at the mean positionCminimum at the mean positionDsame at all positions.

A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will be
View SolutionA block of mass m is attached to a cart of mass 4m through spring of spring constant k as shown in the figure. Friction is absent everywhere. The time period of oscillations of the system, when spring is compressed and then released, is

View Solution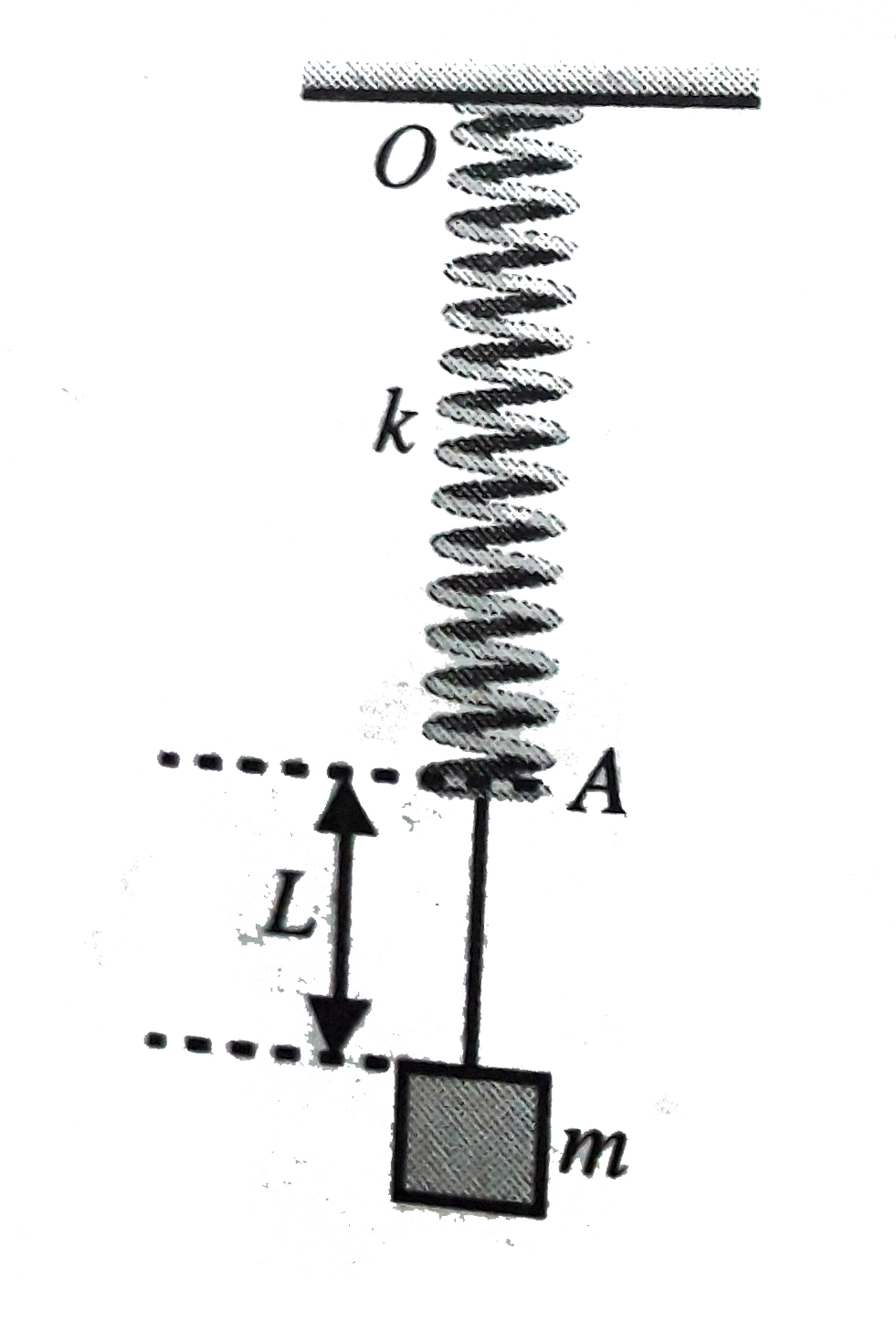
A body of mass m is attached by an inelastic string to a suspended spring of spring constant k. Both the string and the spring have negligible mass and the string is inextensible and of length L. Initially, the mass m is at rest.
Q. If the mass m is now raised up to point A (the top end of the string see fig. and allowed to fall from rest, the maximum extension of the spring in the subsequent motion will be
View SolutionA body of mass m is attached by an inelastic string to a suspended spring of spring constant k. Both the string and the spring have negligible mass and the string is inextensible and of length L. Initially, the mass m is at rest.
The largest amplitude Amax, for which the string will remain taut throughout the motion is
View SolutionA block of mass m, attached to a spring of spring constant k, oscilltes on a smooth horizontal table. The other end of the spring is fixed to a wall. If it has speed v when the spring is at its naturla lenth, how far will it move on the table before coming to an instantaneous rest?
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View Solution