A spring, placed horizontally on a rough surface is compressed by a block of mass m, placed on the same surface so as to store maximum energy in the spring. If the coefficient of friction between the block and the surface is μ, the potential energy stored in the spring is
μ2m2g22k
2μm2g2k
μ2m2g2k
3μ2mg2k
The correct Answer is:A
To solve the problem of finding the potential energy stored in a spring that is compressed by a block on a rough surface, we can follow these steps:
1. Identify Forces Acting on the Block:
- The block of mass m is resting on a rough surface, and it is compressed against a spring. The forces acting on the block include:
- The gravitational force mg acting downward.
- The normal force N acting upward.
- The spring force Fs acting to the right when the spring is compressed.
- The frictional force Ff acting to the left opposing the motion.
2. Establish Vertical Force Balance:
- Since the block is not moving vertically, we can write the equation for the normal force:
N=mg
3. Determine the Limiting Friction:
- The limiting frictional force FL can be expressed as:
FL=μN=μmg
4. Establish Horizontal Force Balance:
- In the horizontal direction, the spring force must equal the frictional force when the block is on the verge of moving:
Fs=Ff
- The spring force can be expressed using Hooke's Law:
Fs=kx0
- Therefore, we have:
kx0=μmg
5. Solve for Maximum Compression x0:
- Rearranging the equation gives us the maximum compression of the spring:
x0=μmgk
6. Calculate the Potential Energy Stored in the Spring:
- The potential energy PE stored in the spring when compressed by x0 is given by:
PE=12kx20
- Substituting x0 into the potential energy formula:
PE=12k(μmgk)2
- Simplifying this expression:
PE=12k⋅μ2m2g2k2=μ2m2g22k
Final Answer:
The potential energy stored in the spring is:
PE=μ2m2g22k
- The block of mass m is resting on a rough surface, and it is compressed against a spring. The forces acting on the block include:
- The gravitational force mg acting downward.
- The normal force N acting upward.
- The spring force Fs acting to the right when the spring is compressed.
- The frictional force Ff acting to the left opposing the motion.
- Since the block is not moving vertically, we can write the equation for the normal force:
N=mg
- The limiting frictional force FL can be expressed as:
FL=μN=μmg
- In the horizontal direction, the spring force must equal the frictional force when the block is on the verge of moving:
Fs=Ff
- The spring force can be expressed using Hooke's Law:
Fs=kx0
- Therefore, we have:
kx0=μmg
- Rearranging the equation gives us the maximum compression of the spring:
x0=μmgk
- The potential energy PE stored in the spring when compressed by x0 is given by:
PE=12kx20
- Substituting x0 into the potential energy formula:
PE=12k(μmgk)2
- Simplifying this expression:
PE=12k⋅μ2m2g2k2=μ2m2g22k
The potential energy stored in the spring is:
PE=μ2m2g22k
Topper's Solved these Questions
- WORK ENERGY AND POWER BOOK - VMC MODULES ENGLISHCHAPTER - WORK ENERGY AND POWER EXERCISE - IMPECCABLE
54 Videos
- WORK ENERGY AND POWER BOOK - VMC MODULES ENGLISHCHAPTER - WORK ENERGY AND POWER EXERCISE - ENABLE
50 Videos
- WAVE MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE ADVANCED ARCHIVE LEVEL 2 (TRUE FALSE TYPE)
4 Videos
Similar Questions
A block of mass m is pulled by a force of constant power P placed on a rough horizontal plane. The friction coefficient between the block and the surface is μ. Then
View SolutionA block of mass m is moving on a rough horizontal surface. μ is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
View SolutionA wooden block of mass M resting on a rough horizontal surface is pulled with a force T at an angle q to the horizontal. If m is coefficient of kinetic friction between the block and the surface, the acceleration of the block is
View SolutionTwo blocks each of mass m are joined together using an ideal spring of force constant K and natural length l0 . The blocks are touching each other when the system is released from rest on a rough horizontal surface. Both the blocks come to rest simultaneously when the extension in the spring is l04. The coefficient of friction between each block and the surface (assuming it to be same between any of the blocks and the surface) is :
View SolutionTwo blocks each of mass m are joined together using an ideal spring of force constant K and natural length l0 . The blocks are touching each other when the system is released from rest on a rough horizontal surface. Both the blocks come to rest simultaneously when the extension in the spring is l04. The coefficient of friction between each block and the surface (assuming it to be same between any of the blocks and the surface) is :
View SolutionA block of mass m is kept on horizontal turn table at x distance from the centre. If coefficient of friction between block and surface of turn table is μ, then maximum angular speed of the table so that block does not slip
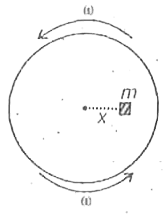
View Solution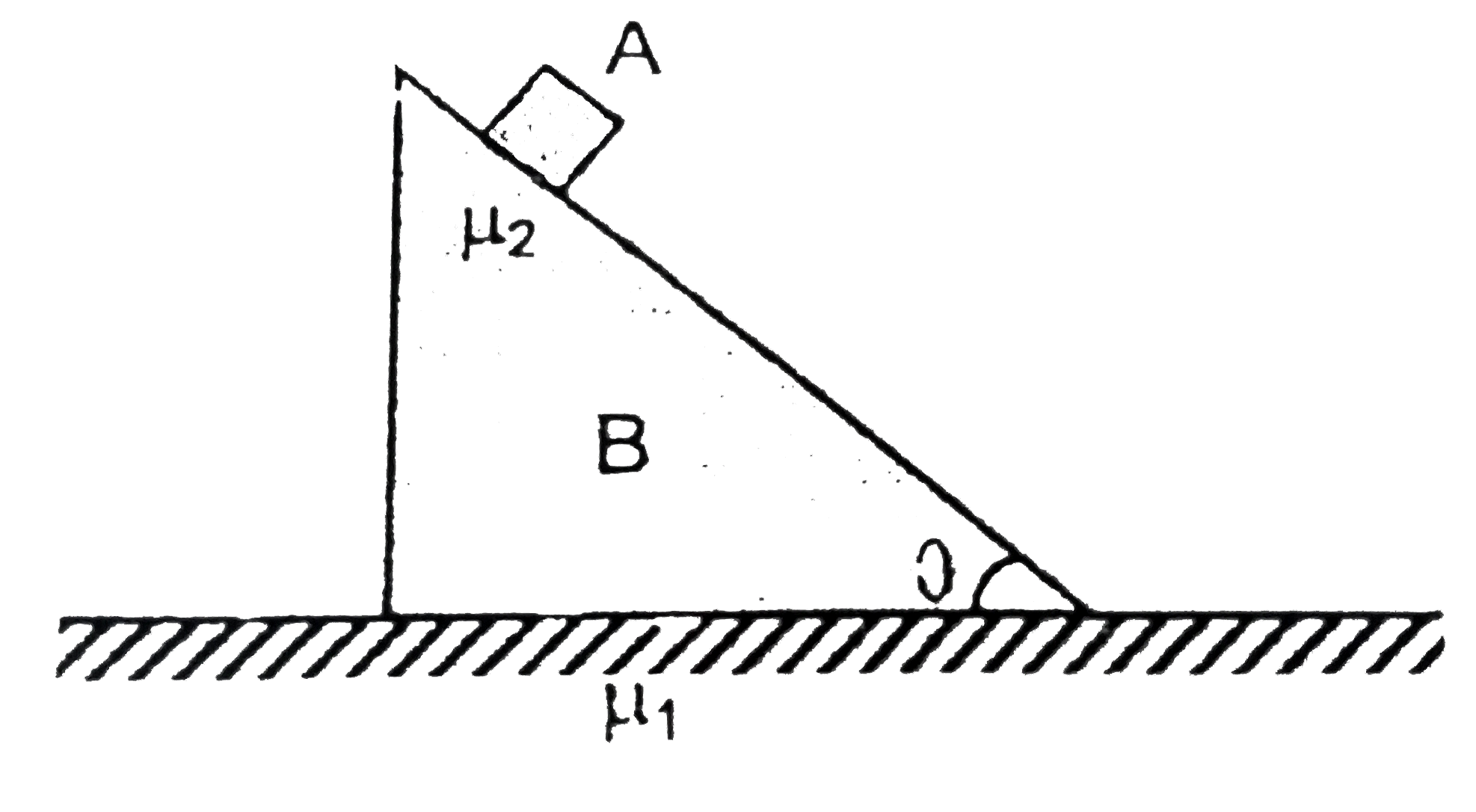
A wedge B of mass 2 m is placed on a rough horizontal suface. The coefficient of friction between wedge and the horizontal surface is μ1. A block of mass m is placed on wedge as shown in the figure. The coefficient of friction between block and wedge is μ2. The block and wedge are released from rest.
Q. Suppose the inclined surface of the wedge is at θ=37∘ from angle from horizontal and μ2=0 are wedge will remain in equilibrium if
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View SolutionTwo spring are connected toa block of mass M placed a frictionless surface as shown if both the spring have a spring constant k the frequency of oscillation block is

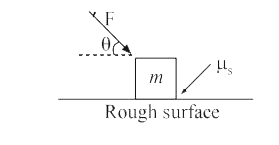
View SolutionWhat is the value of applied force ‘F’ which is exerted at an angle θ with the horizontal on a block of mass ‘m’ placed on a horizontal rough surface, if the coefficient of static friction between the block and the surface is , such that the block is on the verge of moving horizontally?
View Solution