A machine is delivering constant power to drive a body along a straight line. What is the relation between the distance travelled by the body against time ?
(a)s2αt3
(b)s2αt3
(c)s3αt2
(d)sαt3
The correct Answer is:A
To solve the problem of finding the relationship between the distance traveled by a body and time when a machine delivers constant power, we can follow these steps:
1. Understand the Power Equation:
We know that power (P) is defined as the product of force (F) and velocity (v):
P=F⋅v
2. Express Force in Terms of Mass and Acceleration:
The force can be expressed using Newton's second law:
F=m⋅a
where m is the mass of the body and a is its acceleration.
3. Relate Acceleration to Distance and Time:
Acceleration can also be expressed as the change in velocity over time. If we consider distance (s) traveled in time (t), we can express acceleration as:
a=st2
This is derived from the kinematic equation s=12at2 when starting from rest.
4. Substitute Acceleration into the Power Equation:
Now, substituting F and v into the power equation:
- Velocity v can be expressed as v=st.
- Therefore, substituting F and v:
P=(m⋅a)⋅v=m⋅(st2)⋅(st)
Simplifying this gives:
P=m⋅s2t3
5. Rearranging the Equation:
Since power (P) is constant, we can rearrange the equation to find the relationship between distance and time:
s2=P⋅t3m
This shows that s2 is directly proportional to t3:
s2∝t3
6. Conclusion:
The relationship between the distance traveled (s) and time (t) is:
s2=k⋅t3
where k=Pm is a constant.
Final Relation:
Thus, we conclude that the distance squared is directly proportional to the cube of time:
s2∝t3
We know that power (P) is defined as the product of force (F) and velocity (v):
P=F⋅v
The force can be expressed using Newton's second law:
F=m⋅a
where m is the mass of the body and a is its acceleration.
Acceleration can also be expressed as the change in velocity over time. If we consider distance (s) traveled in time (t), we can express acceleration as:
a=st2
This is derived from the kinematic equation s=12at2 when starting from rest.
Now, substituting F and v into the power equation:
- Velocity v can be expressed as v=st.
- Therefore, substituting F and v:
P=(m⋅a)⋅v=m⋅(st2)⋅(st)
Simplifying this gives:
P=m⋅s2t3
Since power (P) is constant, we can rearrange the equation to find the relationship between distance and time:
s2=P⋅t3m
This shows that s2 is directly proportional to t3:
s2∝t3
The relationship between the distance traveled (s) and time (t) is:
s2=k⋅t3
where k=Pm is a constant.
Thus, we conclude that the distance squared is directly proportional to the cube of time:
s2∝t3
Topper's Solved these Questions
Similar Questions
A body starts from rest, what is the ratio of the distance travelled by the body during the 4th and 3rd s?
View SolutionA motor drives a body along a straight line with a constant force. The power P developed by the motor must vary with time t as
View SolutionA body is moved along a straight line by a machine delivering constant power . The distance moved by the body is time t is proptional to
View SolutionA body is moved along a straight line by a machine delivering constant power . The distance moved by the body is time t is proptional to
View SolutionA body is moved along a straight line by a machine delivering constant power . The distance moved by the body is time t is proptional to
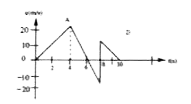
View SolutionThe velocity-time graph of a body moving in a straight line is shown in Fig. Find the displacement and distance travelled by the body in 10 sec.
View SolutionThe variation of velocity of a particle moving along a straight line is shown in the figure. The distance travelled by the particle in 4s is
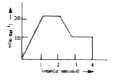
View SolutionThe variation of velocity of a particle moving along a straight line is as shown in the figure given below. The distance travelled by the particle in 5 s is
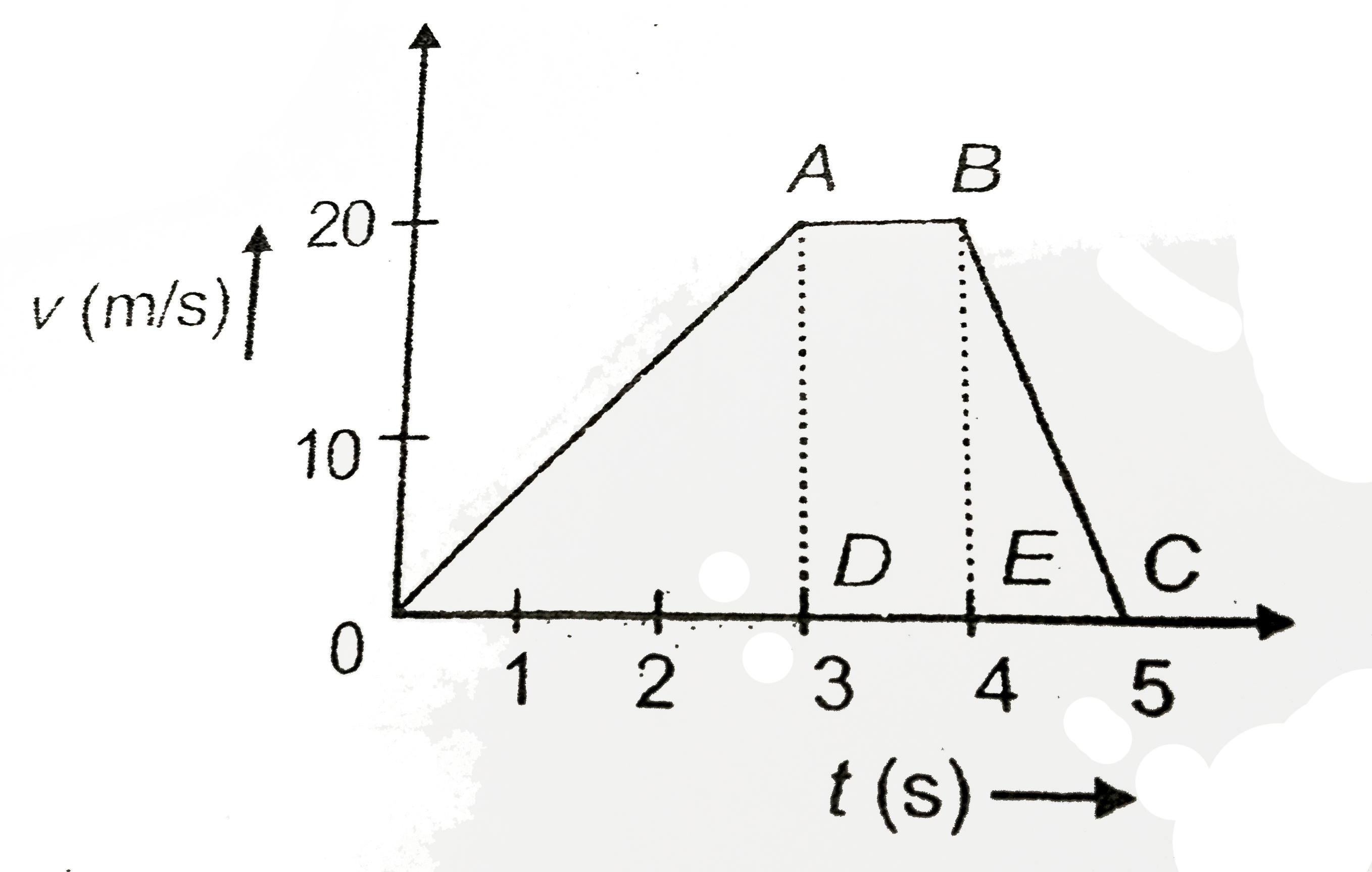
View Solution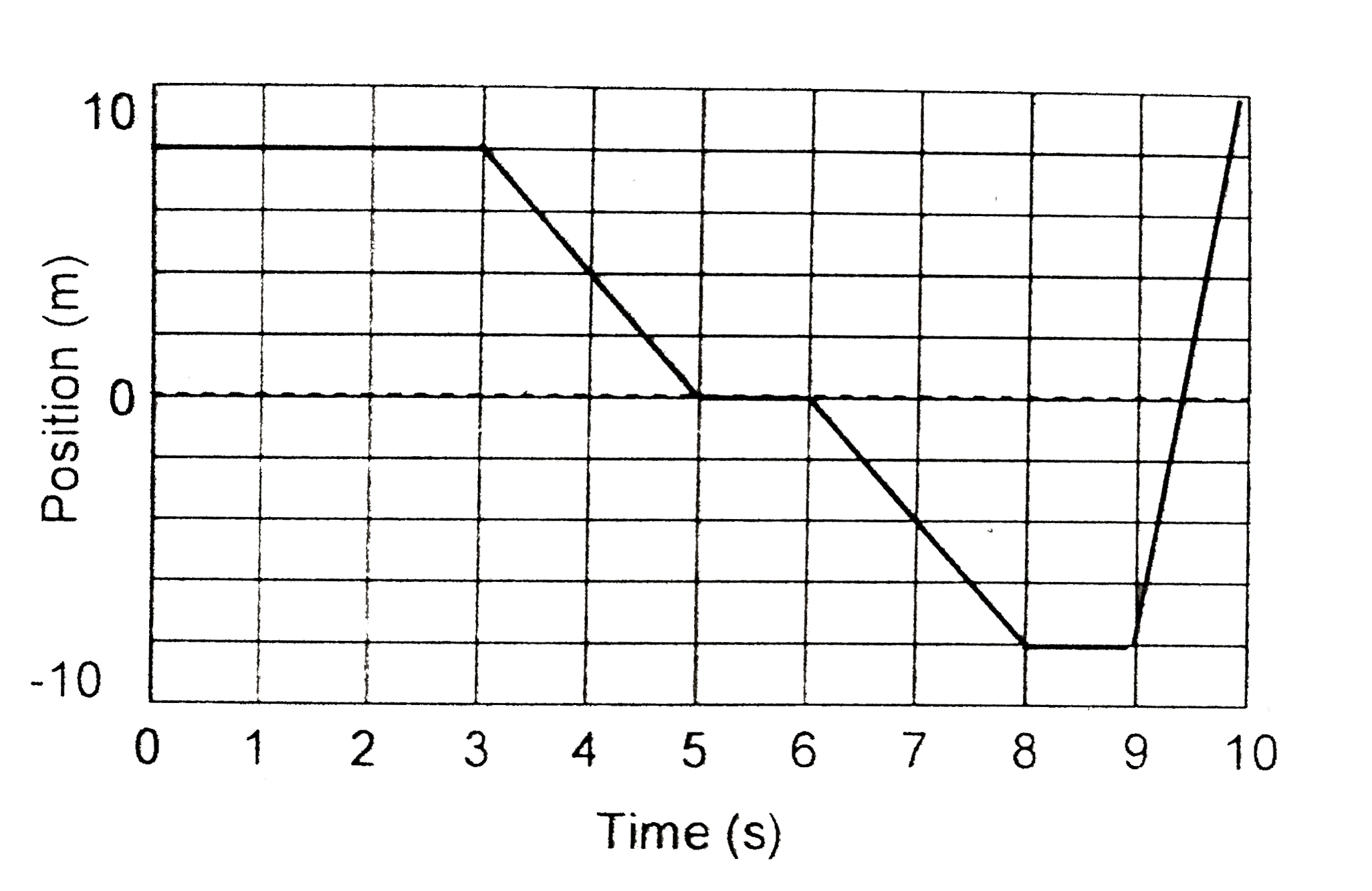
The position versus time graph of a particle moving along a straight line is shown. What is the total distance travelled by the particle from t=0s to t=10s?
View SolutionThe velocity time graph of a body moving in a straight line is shown in the figure. The displacement and distance travelled by the body in 6 sec are respectively.

View Solution
