A long magnet is cut in two parts in such a way that the ratio of their lengths is 2:1. The retio of pole strengths of both the section is
Equal
In the ratio of 2:1
In the ratio of 1:2
In the ratio of 4:1
The correct Answer is:A
To solve the problem of finding the ratio of pole strengths of two sections of a long magnet that is cut in the ratio of 2:1, we can follow these steps:
Step 1: Understand the Concept of Pole Strength
Pole strength (denoted as p) is a measure of the strength of a magnetic pole to attract magnetic materials. It is defined as the magnetic moment per unit length of the magnet.
Step 2: Define the Lengths of the Sections
Let the original length of the magnet be L. When the magnet is cut into two parts in the ratio of 2:1, we can denote the lengths of the two sections as:
- Length of the first section (longer part) = 2L3
- Length of the second section (shorter part) = L3
Step 3: Understand the Magnetic Moment
The magnetic moment (M) of a magnet is given by the product of its pole strength and its length:
M=p×L
Where p is the pole strength and L is the length of the magnet.
Step 4: Analyze the Magnetic Moments of Each Section
Let p1 be the pole strength of the first section and p2 be the pole strength of the second section. The magnetic moments for the two sections can be expressed as:
- For the first section:
M1=p1×2L3
- For the second section:
M2=p2×L3
Step 5: Relate the Magnetic Moments
Since the original magnet is not losing any magnetic moment when cut, we can equate the total magnetic moment before and after cutting:
M=M1+M2
However, since we are interested in the ratio of pole strengths and we know that the total magnetic moment remains constant, we can analyze the relationship between the pole strengths.
Step 6: Calculate the Ratio of Pole Strengths
From the magnetic moment equations, we can express the ratio of the pole strengths:
M1M2=p1×2L3p2×L3=p1×2p2
Since the total magnetic moment remains constant, we can conclude that:
p1×2L3+p2×L3=M
This implies that the pole strengths are directly proportional to the lengths of the sections, thus:
p1p2=21
Conclusion
The ratio of pole strengths of the two sections is:
p1p2=2:1
Pole strength (denoted as p) is a measure of the strength of a magnetic pole to attract magnetic materials. It is defined as the magnetic moment per unit length of the magnet.
Let the original length of the magnet be L. When the magnet is cut into two parts in the ratio of 2:1, we can denote the lengths of the two sections as:
- Length of the first section (longer part) = 2L3
- Length of the second section (shorter part) = L3
The magnetic moment (M) of a magnet is given by the product of its pole strength and its length:
M=p×L
Where p is the pole strength and L is the length of the magnet.
Let p1 be the pole strength of the first section and p2 be the pole strength of the second section. The magnetic moments for the two sections can be expressed as:
- For the first section:
M1=p1×2L3
- For the second section:
M2=p2×L3
Since the original magnet is not losing any magnetic moment when cut, we can equate the total magnetic moment before and after cutting:
M=M1+M2
However, since we are interested in the ratio of pole strengths and we know that the total magnetic moment remains constant, we can analyze the relationship between the pole strengths.
From the magnetic moment equations, we can express the ratio of the pole strengths:
M1M2=p1×2L3p2×L3=p1×2p2
Since the total magnetic moment remains constant, we can conclude that:
p1×2L3+p2×L3=M
This implies that the pole strengths are directly proportional to the lengths of the sections, thus:
p1p2=21
The ratio of pole strengths of the two sections is:
p1p2=2:1
Topper's Solved these Questions
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - ENABLE
50 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - EFFICIENT
50 Videos
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - MCQ
2 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced (Archive) Level - 2 (MATRIX MATCH TYPE)
1 Videos
Similar Questions
If the magnet is cut into four equal parts such that their lengths and breadths are equal . Pole strength of each part is
View SolutionTwo long bar magnets are placed with their axes coinciding in such a way that the north pole of the first magnet is 2.0cm from the south pole of the second. If both the magnets have a pole strength of 10Am, find the force exerted by one magnet on the other.
View SolutionIf a spring of force constant 'k' is cut into two parts, such that one part is thrice in length of the other part. Then the force constant of each part are
View SolutionA magnet is cut into two pieces. Write the poles of the broken pieces of magnets.

View SolutionA bar magnet of moment M and pole strength m is cut into parts of equal lengths. The magetic moment and pole strength of either part is
View SolutionA pole of length 1 m 80 cm is divided into two parts such that their lengths are in the ratio 5:7. Find the length of each part of the pole.
View SolutionA short bar magnet has a magnetic moment of 10 Am2.If its length is 10 cm,then the pole strength of the dipole is
View SolutionA planet travels in an elliptical orbit about a star as shown. At what pair of points is the speed of the planet the same?
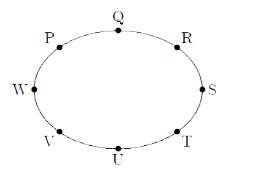
View SolutionA heater coil is cut into two parts of equal length and one of them is used in the leader. The ratio of the heat procued by this half coil to that by the original coil is
View SolutionA spring of force constant K is cut in two parts at its one third length. When both the parts are stretched by same amount, the work done in the two parts, will be :−
View Solution
