An arbitrary shaped closed coil is made of a wire of length L and a current I ampere is flowing in it. If the plane of the coil is perpendicular to megnetic field →B, the force on the coil is
Zero
iBL
2iBL
12iBL
The correct Answer is:A
To find the force on an arbitrary shaped closed coil made of a wire of length L with a current I flowing through it, when the plane of the coil is perpendicular to a magnetic field →B, we can follow these steps:
Step 1: Understanding the Force on a Current-Carrying Wire
The force →F on a current-carrying wire in a magnetic field is given by the formula:
→F=I→L×→B
where →L is the length vector of the wire segment in the direction of the current.
Step 2: Analyzing the Closed Coil
For a closed coil, the total length of the wire is L. However, since the coil is closed, the starting point and the ending point of the wire are the same. Thus, the effective length vector →Leffective for the entire coil is zero because it forms a closed loop.
Step 3: Calculating the Total Force
Since the effective length vector →Leffective is zero, we can substitute this into the force equation:
→F=I→Leffective×→B=I⋅0×→B=0
Conclusion
The total force on the closed coil when the plane of the coil is perpendicular to the magnetic field →B is:
→F=0
Summary
The force on an arbitrary shaped closed coil with a current I in a magnetic field →B is zero due to the closed nature of the coil.
---
The force →F on a current-carrying wire in a magnetic field is given by the formula:
→F=I→L×→B
where →L is the length vector of the wire segment in the direction of the current.
For a closed coil, the total length of the wire is L. However, since the coil is closed, the starting point and the ending point of the wire are the same. Thus, the effective length vector →Leffective for the entire coil is zero because it forms a closed loop.
Since the effective length vector →Leffective is zero, we can substitute this into the force equation:
→F=I→Leffective×→B=I⋅0×→B=0
The total force on the closed coil when the plane of the coil is perpendicular to the magnetic field →B is:
→F=0
The force on an arbitrary shaped closed coil with a current I in a magnetic field →B is zero due to the closed nature of the coil.
Topper's Solved these Questions
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - EFFICIENT
50 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IMPECCABLE
53 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IN-CHAPTER EXERCISE-K
10 Videos
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - MCQ
2 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced (Archive) Level - 2 (MATRIX MATCH TYPE)
1 Videos
Similar Questions
A circular coil having N turns is made from a wire of length L meter. If a current I ampere is passed through it and is placed in amagnetic field of B Tesla, the maximum torque on it is
View SolutionIf plane of coil and uniform magnetic field B(4T0 is same then torque on the current carrying coil is

View SolutionA wire of length l is bent in the form a circular coil of some turns. A current I flows through the coil. The coil is placed in a uniform magnetic field B. The maximum torqur on the coil can be
View SolutionA current I flows along a thin wire shaped as shown in figure. The radius of the curved part of the wire is r. The field at the centre O of the coil is:
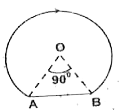
View SolutionCurrent 'i' is flowing in heaxagonal coil of side a. The magnetic induction at the centre of the coil will be
View SolutionA flip coil consits of N turns of circular coils which lie in a uniform magnetic field. Plane of the coils is perpendicular to the magnetic field as shown in figure. The coil is connected to a current integrator which measures the total charge passing through it. The coil is turned through 180∘ about the diameter. The charge passing through the coil is
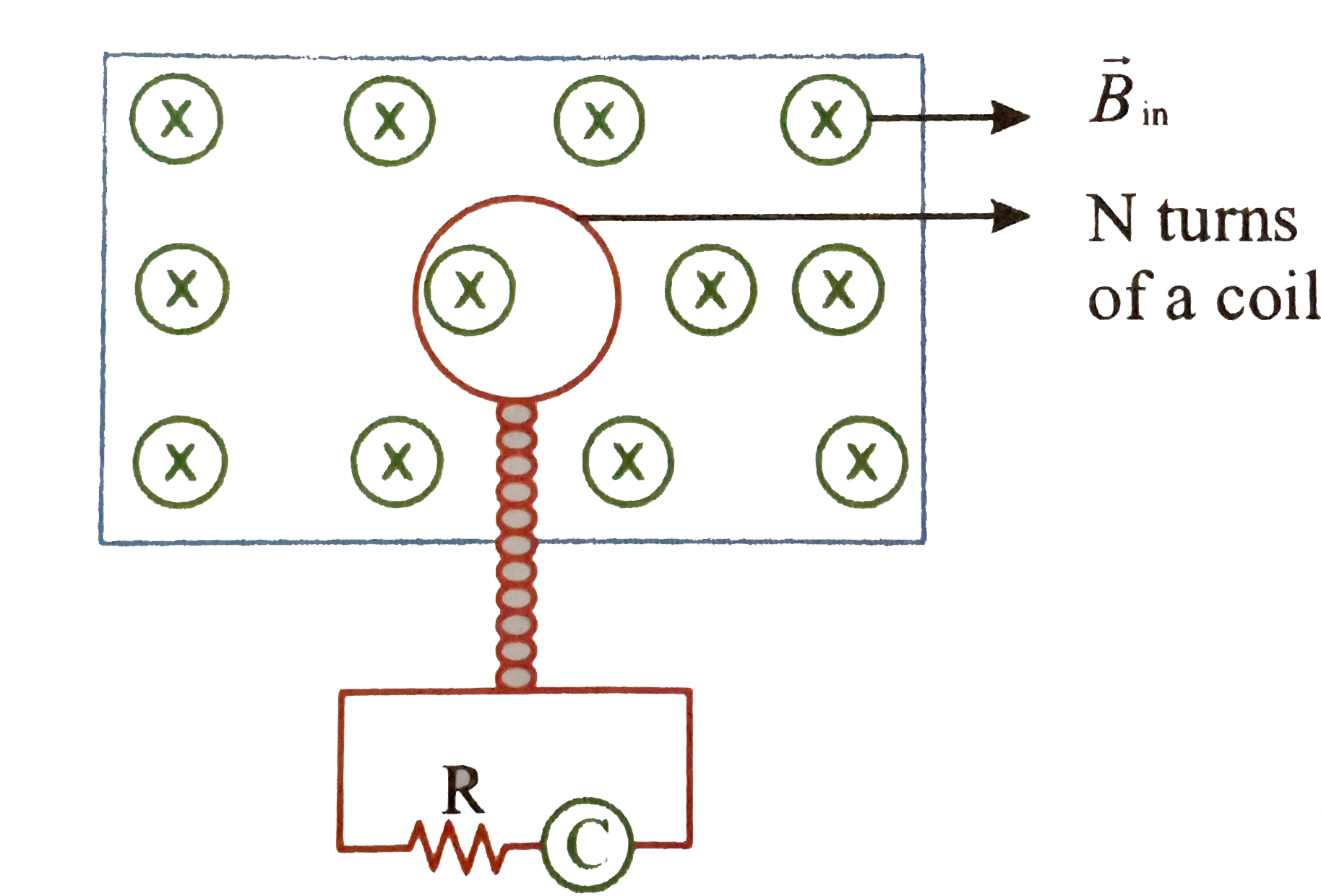
View SolutionA small coil of N turns has area A and a current I flows through it. The magnetic dipole moment of this coil will be
View SolutionA conductor of length L and carrying current i is bent to form a coil of two turns.Magnetic field at the centre of the coil will be
View SolutionA coil of self-inductance L is placed in an external magnetic field (no current flows in the coil). The total magnetic flux linked with the coil is ϕ. The magnetic field energy stored in the coil is
View SolutionCurrent i is carried in a wire of length L. If the wire is turned into a circular coil, the maximum magnitude of torque in a given magnetic field B will be
View Solution
