Points A and B are situated perpendicular to the axis of a 2cm long bar magnet at large distances X and 3X from its centre on opposite sides. The retio of the magnetic fields at A and B wil be approximately equal to
1:9
2:9
27:1
9:1
The correct Answer is:C
To solve the problem, we need to find the ratio of the magnetic fields at points A and B, which are located at distances X and 3X from the center of a bar magnet, respectively.
1. Understanding the Magnetic Field of a Bar Magnet:
The magnetic field (B) at a point on the axis of a bar magnet is given by the formula:
B=μ0m4πd3
where μ0 is the permeability of free space, m is the magnetic moment of the bar magnet, and d is the distance from the center of the magnet to the point where the magnetic field is being calculated.
2. Identify Distances:
- For point A, the distance from the center of the magnet is dA=X.
- For point B, the distance from the center of the magnet is dB=3X.
3. Calculate Magnetic Field at Point A:
Using the formula for the magnetic field:
BA=μ0m4π(X)3
4. Calculate Magnetic Field at Point B:
Similarly, for point B:
BB=μ0m4π(3X)3
Simplifying this gives:
BB=μ0m4π(27X3)=μ0m108πX3
5. Finding the Ratio of Magnetic Fields:
Now, we need to find the ratio BABB:
BABB=μ0m4πX3μ0m108πX3
The μ0m and πX3 cancel out:
BABB=1084=27
6. Final Ratio:
Thus, the ratio of the magnetic fields at points A and B is:
BA:BB=27:1
Conclusion:
The ratio of the magnetic fields at points A and B is approximately equal to 27:1.
The magnetic field (B) at a point on the axis of a bar magnet is given by the formula:
B=μ0m4πd3
where μ0 is the permeability of free space, m is the magnetic moment of the bar magnet, and d is the distance from the center of the magnet to the point where the magnetic field is being calculated.
- For point A, the distance from the center of the magnet is dA=X.
- For point B, the distance from the center of the magnet is dB=3X.
Using the formula for the magnetic field:
BA=μ0m4π(X)3
Similarly, for point B:
BB=μ0m4π(3X)3
Simplifying this gives:
BB=μ0m4π(27X3)=μ0m108πX3
Now, we need to find the ratio BABB:
BABB=μ0m4πX3μ0m108πX3
The μ0m and πX3 cancel out:
BABB=1084=27
Thus, the ratio of the magnetic fields at points A and B is:
BA:BB=27:1
The ratio of the magnetic fields at points A and B is approximately equal to 27:1.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - EFFICIENT50videos
MOVING CHARGES & MAGNETISM
- BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IMPECCABLE53videos
MOVING CHARGES & MAGNETISM
- BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IN-CHAPTER EXERCISE-K10videos
MOVING CHARGES & MAGNETISM
- BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - MCQ2videos
Motion in Two Dimensions
- BOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced (Archive) Level - 2 (MATRIX MATCH TYPE)1videos
PROPERTIES OF MATTER
Similar Questions
Point A and B are situated along the extended axis of 2cm long bar magnet at a distance x and 2xcm respectively. From the pole nearer to the points, the ratio of the magnetic field at A and B will be
View SolutionA bar magnet of length 3cm has points A and B along its axis at distance of 24cm and 48cm on the opposite sides. Ratio of magnetic field at these points will be
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The magnitude of the equatorial magnetic field due to a bar magnet of length 2 cm at a distance of 1m from its mid-point is (magnetic moment of the bar magnet is 0.60 A m)
A5.0×10−5 TB6.0×10−8 TC7.0×10−7 TD8.0×10−8 T
Two long parallel wire A and B situated perpendicuilar to the plane of the paper at a distance 2a are carrying equal currents I in opposite direction as show in the figure . The value of magnetic induction at point P situated at equal distance r from both the wires will be
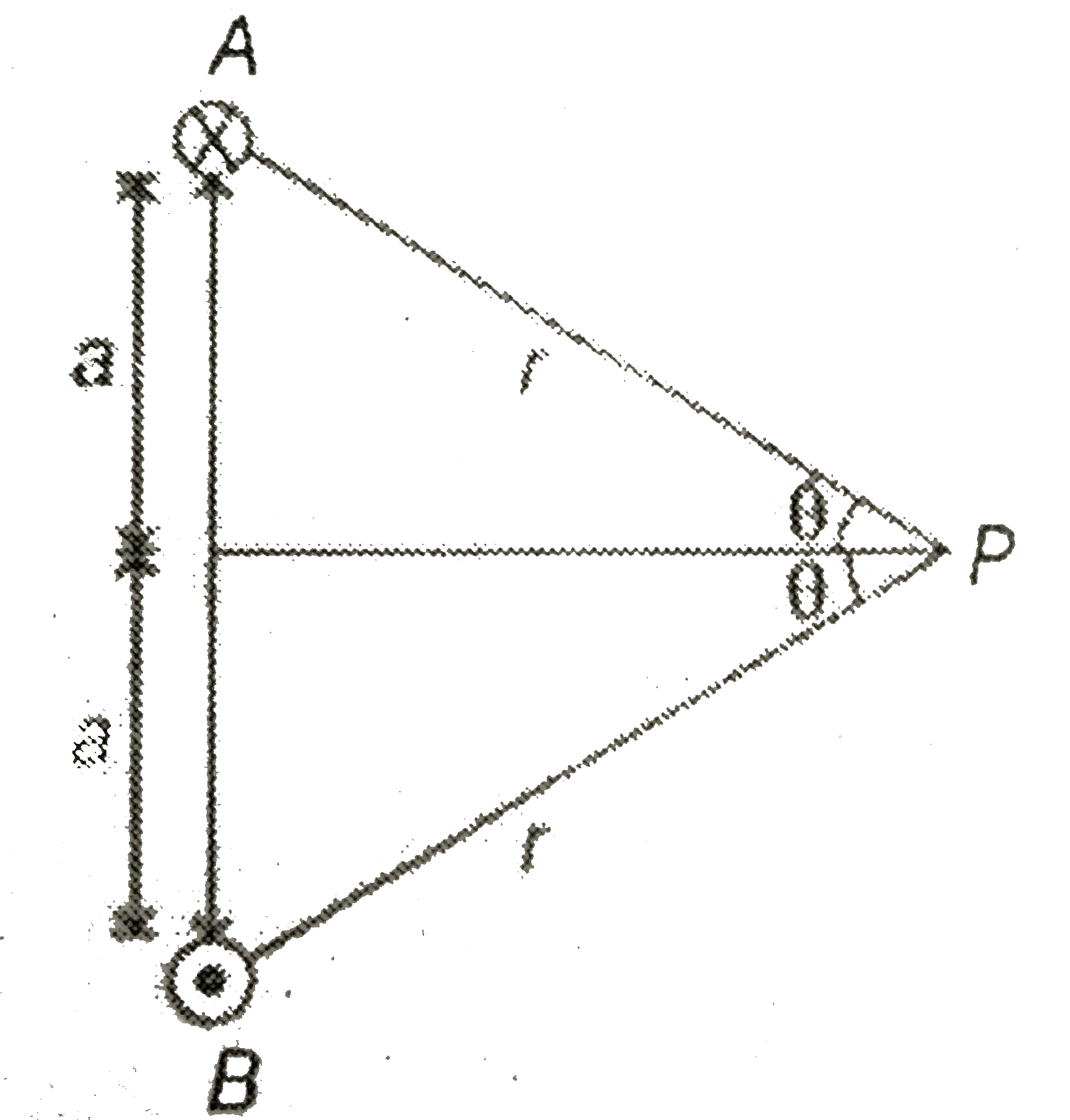 View Solution
View SolutionA circular coil of radius R carries a current i. The magnetic field at its centre is B. The distance from the centre on the axis of the coil where the magnetic field will be B/8 is
View SolutionThe magnetic field on the axis at a distance z from the centre of the bar magnet would be ?
View SolutionLet r be the distance of a point on the axis of a bar magnet from its center. The magnetic field at such a point is proportional to
View SolutionLet r be the distance of a point on the axis of a magnetic dipole from its centre. The magnetic field at such a point is proportional to
View SolutionLet r be the distance of a point on the axis of a magnetic dipole from its centre. The magnetic field at such a point is proportional to
View SolutionIf r be the distance of a point on the axis of a magnetic dipole from its centre them the magnetic field at such a point is proportional to
View Solution

