A thin bar magnet of length 2L is bent at the mid point, so that the angle between them is 60∘.Find the new length of the magnet.
√2L
√3L
2L
L
The correct Answer is:D
To find the new length of a thin bar magnet that has been bent at its midpoint to form an angle of 60 degrees, we can follow these steps:
Step 1: Understand the Initial Configuration
The initial length of the bar magnet is given as 2L. When it is bent at the midpoint, each half of the magnet will have a length of L.
Step 2: Visualize the Bending
When the magnet is bent at the midpoint to form an angle of 60 degrees, we can visualize the two halves of the magnet forming a "V" shape. Each half makes an angle of 30 degrees with the vertical line drawn from the midpoint.
Step 3: Calculate the New Length
To find the new effective length of the magnet, we can use the cosine of the angle formed by each half of the magnet with respect to the vertical.
The new length L′ can be calculated using the formula:
L′=Lcos(30∘)+Lcos(30∘)
Since there are two halves, we multiply the length of one half by 2.
Step 4: Substitute the Cosine Value
We know that:
cos(30∘)=√32
Thus, substituting this value into our equation:
L′=2Lcos(30∘)=2L(√32)
This simplifies to:
L′=L√3
Step 5: Conclusion
The new length of the magnet after bending is:
L′=L√3
The initial length of the bar magnet is given as 2L. When it is bent at the midpoint, each half of the magnet will have a length of L.
When the magnet is bent at the midpoint to form an angle of 60 degrees, we can visualize the two halves of the magnet forming a "V" shape. Each half makes an angle of 30 degrees with the vertical line drawn from the midpoint.
To find the new effective length of the magnet, we can use the cosine of the angle formed by each half of the magnet with respect to the vertical.
L′=Lcos(30∘)+Lcos(30∘)
Since there are two halves, we multiply the length of one half by 2.
We know that:
cos(30∘)=√32
Thus, substituting this value into our equation:
L′=2Lcos(30∘)=2L(√32)
This simplifies to:
L′=L√3
The new length of the magnet after bending is:
L′=L√3
Topper's Solved these Questions
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - EFFICIENT
50 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IMPECCABLE
53 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IN-CHAPTER EXERCISE-K
10 Videos
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - MCQ
2 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced (Archive) Level - 2 (MATRIX MATCH TYPE)
1 Videos
Similar Questions
A thin rod of length L and mass M is bent at its midpoint into two halves so that the angle between them is 90∘. The moment of inertia of the bent rod about an axis passing through the bending point and perpendicular to the plane defined by the two halves of the rod is.
View SolutionA wire of length 21 is bent al mid point so that the angle between two halves is 60∘. If it moves as shown with a velocity v in a magnetic field B find the induced emf

View Solution
Knowledge Check
If line l1 intersects another line l2 at its mid-point in such a way that the angle between them is 90∘ , then the line _____ is called the _______ of the line ______
Al1, perpendicular bisector, l2Bl2, perpendicular bisector, l1Cl1, l2, perpendicular bisectorDl1, l3, perpendicular bisector
A wire of length .2l. is bent at midpoint so that angle between the two halves is 60∘. If it moves as shown with velocity .V. in a magnetic field .B.. The induced emf with be
View SolutionA thin rod of length L of mass M is bent at the middle point O at an angle of 60∘. The moment of inertia of the rod about an axis passing through O and perpendicular to the plane of the rod will be

View SolutionWhen a current carrying conductor is placed in a magnetic field, it experiences a mechanical force. What should be the angle between the magnetic field and the length of the conductor so that the force experienced is :
(i) Zero
(ii) Maximum ?
View SolutionMagnetic length of a bar magnet is
View SolutionA metallic V shaped rod OAC is rotated with respect to one of its end in uniform magnetic field, such that axis of rotation is parallel to the direction of magnetic field. Length of each arm of rod is L and angle between the arms is 60∘. P is the mid-point of section AC. Magnitude of magnetic field is B. Then choose the correct relation:
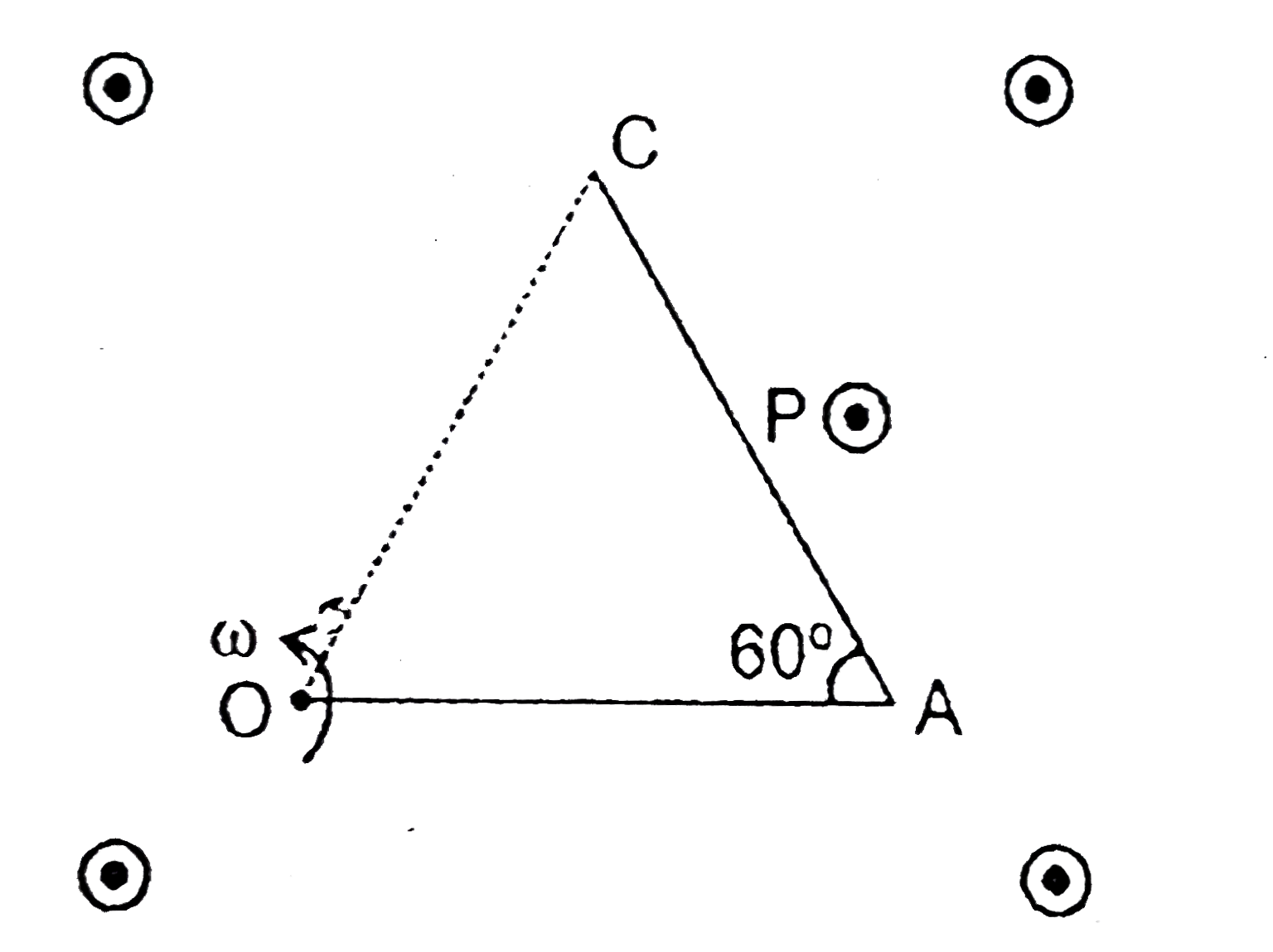
View SolutionA metallic V shaped rod OAC is rotated with respect to one of its end in uniform magnetic field, such that axis of rotation is parallel to the direction of magnetic field. Length of each arm of rod is L and angle between the arms is 60∘. P is the mid-point of section AC. Magnitude of magnetic field is B. Then choose the correct relation:

View SolutionFind magnetic field at point P shown in Fig. point P is on the bisector of angle between the wires.
View Solution
