An electron falling freely under gravity entersa region of uniform horizontal magnetic field pointing north to south. The particle will be deflected towards
east
west
north
south
The correct Answer is:A
To solve the problem, we need to analyze the motion of an electron in a magnetic field. The steps are as follows:
Step 1: Identify the Directions
- The electron is falling freely under gravity, which means its velocity is directed downward (towards the ground).
- The magnetic field is uniform and directed from north to south.
Step 2: Determine the Charge of the Particle
- The particle in question is an electron, which has a negative charge (Q = -e).
Step 3: Use the Right-Hand Rule
- The magnetic force acting on a charged particle moving in a magnetic field is given by the equation:
→F=Q(→V×→B)
where:
- →F is the magnetic force,
- Q is the charge of the particle,
- →V is the velocity of the particle,
- →B is the magnetic field.
Step 4: Apply the Right-Hand Rule
- For a positive charge, you would use your right hand:
- Point your fingers in the direction of the velocity (downward).
- Curl them in the direction of the magnetic field (from north to south).
- Your thumb will point in the direction of the force.
- Since the electron is negatively charged, the force will be in the opposite direction of what the right-hand rule indicates.
Step 5: Determine the Resulting Direction
- If we apply the right-hand rule for the velocity (downward) and the magnetic field (north to south), the thumb points towards the west for a positive charge.
- However, since the electron is negatively charged, the magnetic force will be directed opposite to this, which means the force will be directed towards the east.
Conclusion
Thus, the electron will be deflected towards the east.
- The electron is falling freely under gravity, which means its velocity is directed downward (towards the ground).
- The magnetic field is uniform and directed from north to south.
- The particle in question is an electron, which has a negative charge (Q = -e).
- The magnetic force acting on a charged particle moving in a magnetic field is given by the equation:
→F=Q(→V×→B)
where:
- →F is the magnetic force,
- Q is the charge of the particle,
- →V is the velocity of the particle,
- →B is the magnetic field.
- For a positive charge, you would use your right hand:
- Point your fingers in the direction of the velocity (downward).
- Curl them in the direction of the magnetic field (from north to south).
- Your thumb will point in the direction of the force.
- Since the electron is negatively charged, the force will be in the opposite direction of what the right-hand rule indicates.
- If we apply the right-hand rule for the velocity (downward) and the magnetic field (north to south), the thumb points towards the west for a positive charge.
- However, since the electron is negatively charged, the magnetic force will be directed opposite to this, which means the force will be directed towards the east.
Thus, the electron will be deflected towards the east.
Topper's Solved these Questions
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IMPECCABLE
53 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - Illustration
55 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - ENABLE
50 Videos
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - MCQ
2 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced (Archive) Level - 2 (MATRIX MATCH TYPE)
1 Videos
Similar Questions
A negative charged particle falling freely under gravity enters a region having uniform horizontal magnetic field pointing towards north.The particle will be deflected towards
View SolutionA positively charged particle moving due east enters a region of uniform magnetic field directed vertically upwards. The partical will be
View SolutionA neutron, a proton, an electron and an α−particle enter a region of uniform magnetic field with equal velocities. The magnetic field is perpendicular to the paper and directed into it. The tracks of particles are labeled in Fig. 1.132. The neutron follows the track

View SolutionAn electron does not suffer any deflection while passing through a region of uniform magnetic field. What is the direction of the magnetic field ?
View SolutionAn electron travelling horizontally towards west enters into a magnetic field acting vertically down wards. It deflects towards
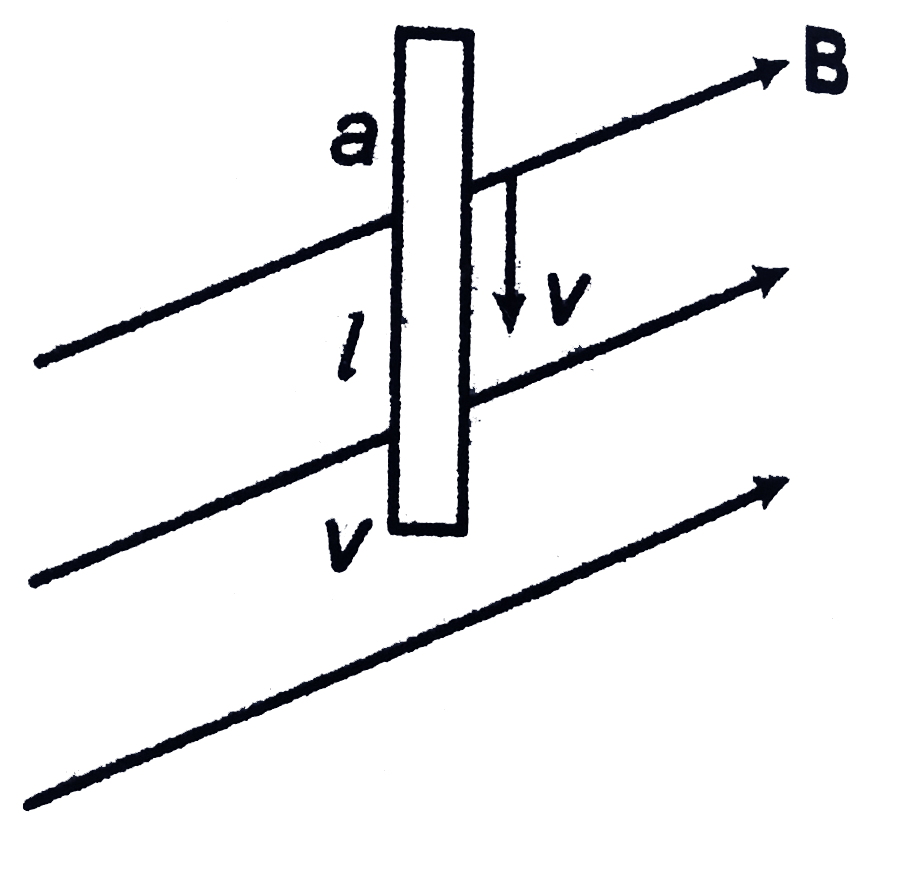
View SolutionA conducting rod of length l falls verticaly under gravity in a region of uniform magnetic field B. The field vectors are inclined at an angle θ with the horizontal as shown in figure. If the instantaneous velocity of the rod is v, the induced emf in the rod ab is
View SolutionIn a region where both non-zero uniform electric field and magnetic field coexist, the path of a charged particle
View SolutionA proton and an electron are projected into a region of uniform magnetic field in a direction perpendicular to the field. If they have the same initial velocities then
View SolutionA charged particle is released from rest in a region of steady and uniform electric and magnetic fields which are parallel to each other . The particle will remove in a
View SolutionA charged particle is released from rest in a region of steady and uniform electric and magnetic fields which are parallel to each other . The particle will remove in a
View Solution
