Consider metal ring kept on a horizontal plane . A bar magnet is held above the ring with its length along the axis is held above the ring with its length along the axis of the ring . If the magnet is dropped freely the acceleration of the falling magnet is : ( g is accelration due to gravity )
(a)More than g
(b)Equal to g
(c)Less than g
(d)Depends on mass of magnet
The correct Answer is:C
To solve the problem of determining the acceleration of a falling magnet above a metal ring, we can follow these steps:
Step 1: Understand the Setup
We have a metal ring placed on a horizontal plane and a bar magnet held above it. The magnet is oriented such that its length is along the axis of the ring.
Hint: Visualize the setup to understand how the magnet and the ring interact.
Step 2: Consider the Forces Acting on the Magnet
When the magnet is dropped, it experiences two main forces:
1. The gravitational force acting downward (mg, where m is the mass of the magnet and g is the acceleration due to gravity).
2. An induced magnetic force due to the change in magnetic flux through the ring as the magnet falls.
Hint: Remember that the gravitational force is constant, but the induced force will depend on the motion of the magnet.
Step 3: Analyze the Induced EMF
As the magnet falls, it changes the magnetic flux linked with the metal ring. According to Faraday's law of electromagnetic induction, a change in magnetic flux induces an electromotive force (EMF) in the ring. This induced EMF creates a current in the ring, which in turn generates a magnetic field that opposes the motion of the falling magnet (Lenz's Law).
Hint: Recall that Lenz's Law states that the direction of induced current will always oppose the change in magnetic flux.
Step 4: Determine the Effect on Acceleration
The induced magnetic force acts upward against the gravitational force. Therefore, the net force acting on the magnet will be less than the gravitational force. This results in a net downward acceleration that is less than g.
Hint: Use Newton's second law (F = ma) to relate the net force to the acceleration of the magnet.
Step 5: Conclusion
Since the upward induced force opposes the downward gravitational force, the acceleration of the falling magnet will be less than g. Hence, we conclude that the acceleration of the falling magnet is less than the acceleration due to gravity.
Final Answer: The acceleration of the falling magnet is less than g.
Summary of Steps:
1. Visualize the setup with the magnet and the ring.
2. Identify the forces acting on the magnet.
3. Analyze the induced EMF and its effects.
4. Conclude that the net force results in an acceleration less than g.
We have a metal ring placed on a horizontal plane and a bar magnet held above it. The magnet is oriented such that its length is along the axis of the ring.
When the magnet is dropped, it experiences two main forces:
1. The gravitational force acting downward (mg, where m is the mass of the magnet and g is the acceleration due to gravity).
2. An induced magnetic force due to the change in magnetic flux through the ring as the magnet falls.
As the magnet falls, it changes the magnetic flux linked with the metal ring. According to Faraday's law of electromagnetic induction, a change in magnetic flux induces an electromotive force (EMF) in the ring. This induced EMF creates a current in the ring, which in turn generates a magnetic field that opposes the motion of the falling magnet (Lenz's Law).
The induced magnetic force acts upward against the gravitational force. Therefore, the net force acting on the magnet will be less than the gravitational force. This results in a net downward acceleration that is less than g.
Since the upward induced force opposes the downward gravitational force, the acceleration of the falling magnet will be less than g. Hence, we conclude that the acceleration of the falling magnet is less than the acceleration due to gravity.
1. Visualize the setup with the magnet and the ring.
2. Identify the forces acting on the magnet.
3. Analyze the induced EMF and its effects.
4. Conclude that the net force results in an acceleration less than g.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE
52 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - ENABLE
50 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - IN-CHAPTER EXERCISE-G
10 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)
89 Videos
Similar Questions
Knowledge Check
A metal ring is held horizontally and bar magnet is dropped through the ring with its length along the axis of the ring. The acceleration of the falling magnet
Aequal to gBless than gCmore than gDdepends of on the diameter of the ring length of magnet
In the figure shown, the magnet is pushed towards the fixed ring along the axis of the ring and it passes through the ring.
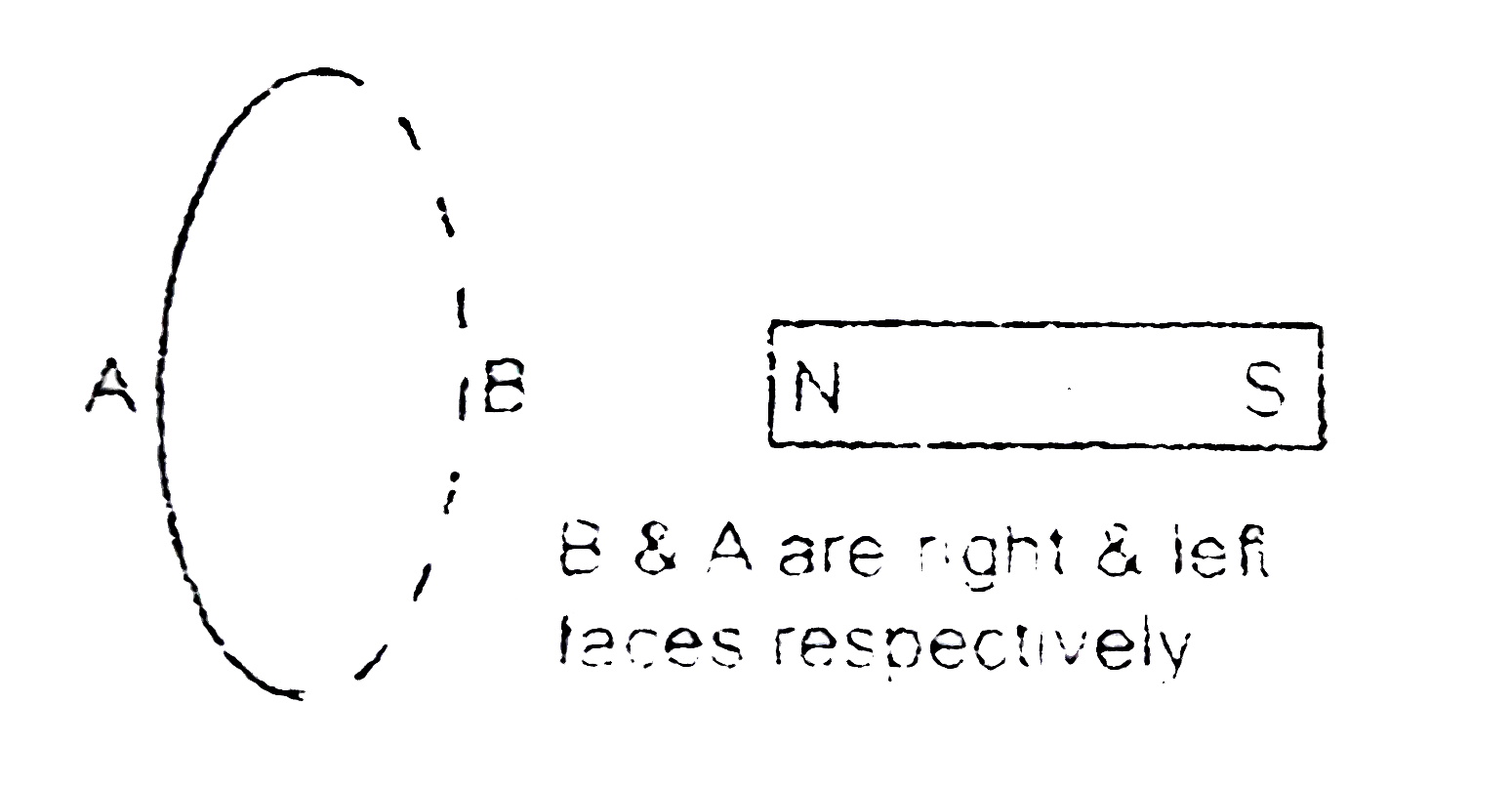
View SolutionA cylindrical bar magnet is kept along the axis of a circular coil. If the magnent is rotated about its axis, then
View SolutionA current carrying ring is placed in a horizontal plane. A charged particle is dropped along the axis of the ring to fall under the influence of gravity
View Solutionshows a horizontal solenoid connected to a battery and a switch. A coper ring is placed on a frictionless track, the axis of the ring being along the axis of the solenoid. As the switch is closed, the ring will

View SolutionA metallic ring with a small cut is held horizontally and a magnet is allowed to fall vertically through the ring then the acceleration of the magnet is :
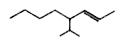
View SolutionWrite down the IUPAC name of the following :
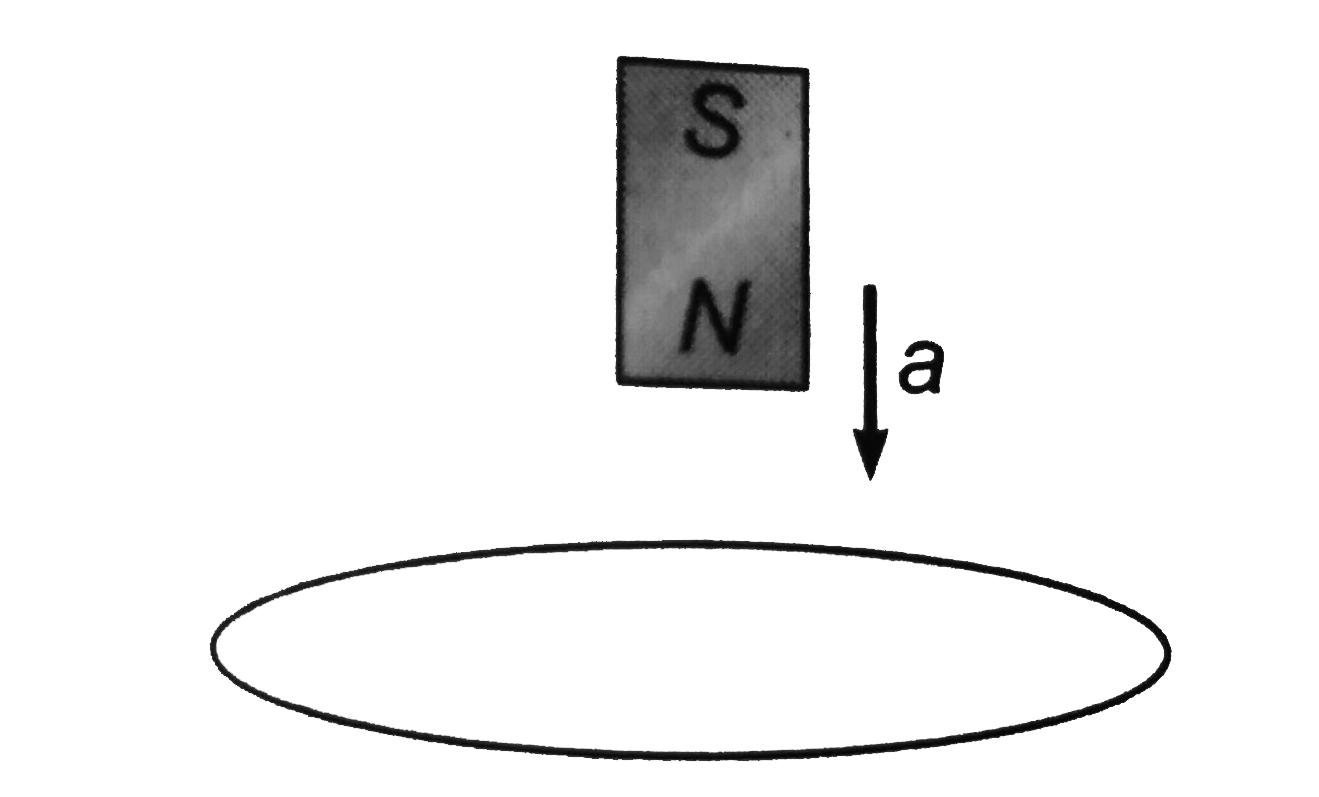
View SolutionA bar magnet is freel falling along the axis of a circular loop as shown in Figure. State whether its acceleration a is equal to greater than or less than the acceleration due to gravity g.
View Solution
