When a beam of light goes from denser medium (μd) to rarer medium (μr), then it is generally observed that magnitude of angle of incidence is half that of angle of refraction. Then magnitude of incident angle will be-(here μ=μd/μr)
2sin−1(μ2)
2cos−1μ
cos−1(μ2)
2cos−1(μ2)
The correct Answer is:D
To solve the problem, we will follow these steps:
Step 1: Understand the relationship between angles of incidence and refraction
Given that the angle of incidence I is half of the angle of refraction R, we can express this relationship as:
I=R2
or equivalently,
R=2I
Step 2: Apply Snell's Law
Snell's Law states that:
sinIsinR=μrμd
Given that μ=μdμr, we can rewrite μrμd as 1μ. Thus, we have:
sinIsinR=1μ
Step 3: Substitute for R
Substituting R=2I into Snell's Law gives us:
sinIsin(2I)=1μ
Step 4: Use the double angle formula
Using the double angle formula for sine, we know that:
sin(2I)=2sinIcosI
Substituting this into our equation from Step 3, we get:
sinI2sinIcosI=1μ
Step 5: Simplify the equation
Cancelling sinI from both sides (assuming sinI≠0):
12cosI=1μ
Cross-multiplying gives:
μ=2cosI
Step 6: Solve for I
Rearranging the equation gives:
cosI=μ2
To find I, we take the inverse cosine:
I=cos−1(μ2)
Final Result
Thus, the magnitude of the incident angle I is:
I=cos−1(μ2)
Given that the angle of incidence I is half of the angle of refraction R, we can express this relationship as:
I=R2
or equivalently,
R=2I
Snell's Law states that:
sinIsinR=μrμd
Given that μ=μdμr, we can rewrite μrμd as 1μ. Thus, we have:
sinIsinR=1μ
Substituting R=2I into Snell's Law gives us:
sinIsin(2I)=1μ
Using the double angle formula for sine, we know that:
sin(2I)=2sinIcosI
Substituting this into our equation from Step 3, we get:
sinI2sinIcosI=1μ
Cancelling sinI from both sides (assuming sinI≠0):
12cosI=1μ
Cross-multiplying gives:
μ=2cosI
Rearranging the equation gives:
cosI=μ2
To find I, we take the inverse cosine:
I=cos−1(μ2)
Thus, the magnitude of the incident angle I is:
I=cos−1(μ2)
Topper's Solved these Questions
- RAY OPTICS AND WAVE OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS AND WAVE OPTICS EXERCISE - ENABLE
50 Videos
- RAY OPTICS AND WAVE OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS AND WAVE OPTICS EXERCISE - EFFICIENT
49 Videos
- RAY OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - IN-CHAPTER EXERCISE-J
10 Videos
- REVISION TEST-15 JEE - 2020BOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-15 JEE - 2020EXERCISE - PHYSICS
25 Videos
Similar Questions
When a ray of light travles from an optically more denser medium to an optically less denser medium, the angle of incidence is always _____ than the angle of refraction.
View SolutionWhen a ray of light travels from an optically less denser medium to an optically more denser medium, the angle of incidence is always less than angle of refraction.
View SolutionA ray of light passes from vaccum into a medium of refractive index n. If the angle of incidence is twice the angle of refraction, then the angle of incidence is
View SolutionA light ray is incident fromt a denser medium on the boundary separating it from a rarer medium at an angle of incidence equal to the critical angle. What is the angle of refraction for the ray ?
View SolutionLight from a denser medium 1 passes to a rarer medium 2. When the angle of incidence is θ the partially reflected and refracted rays are mutually perpendicular. The critical angle will be

View SolutionA ray of light from a denser medium strikes a rare medium as shown in figure. The reflected and refracted rays make an angle of 90∘ with each other. The angles of reflection and refraction are r and r'. The critical angle would be

View SolutionIn the diagrams given in Figure C, draw the angle of incidence and the angle of refraction. Identify which medium is rarer and which medium is denser.
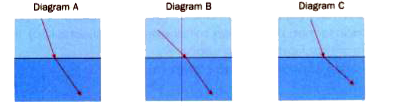
View SolutionLight falls from glass (μ=1.5) to air. Find the angle of incidence for which the angle of deviation is 90∘.
View Solution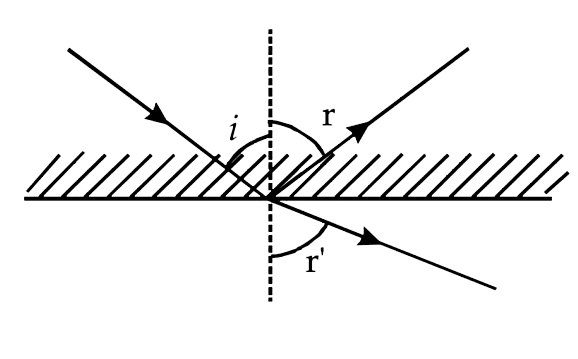
A ray of light from a denser medium strike a rarer medium at an angle of incidence I (see Fig). The reflected and refracted rays make as angle of 90degrees with each other. The angles of reflection and refraction are r and r The critical angle is
View SolutionA ray of light is incident at an angle i from denser to rare medium. The reflected and the refracted rays are mutually perpendicular. The angle of reflection and the angle of refraction are respectively r and r'. Then the critical angle will be:
View Solution
