A concave mirror of radius of curvature 60 cm is placed at the bottom of tank containing water upto a height of 20 cm. The mirror faces upwards with its axis vertical. Solar light falls normally on the surface of water and the image of the sun is formed. If aμw=43 then with the observer in air, the distance of the image from the surface of water is:
30 cm
10 cm
7.5 cm above
7.5 cm below
The correct Answer is:C
To solve the problem step by step, we will follow the principles of optics, particularly focusing on the behavior of concave mirrors and the effect of a medium (water) on the light rays.
1. Identify the Radius of Curvature and Focal Length:
- The radius of curvature (R) of the concave mirror is given as 60 cm.
- The focal length (f) of a concave mirror is given by the formula:
f=R2
- Therefore,
f=60cm2=30cm
Hint: Remember that for concave mirrors, the focal length is negative, but since we are dealing with distances, we will use the absolute value for calculations.
2. Determine the Real Depth:
- The depth of water in the tank is 20 cm. The distance from the mirror to the surface of the water is the focal length minus the height of the water:
Real Depth=f−Height of Water=30cm−20cm=10cm
Hint: The real depth is the distance from the mirror to the water surface, which is the focal length minus the height of the water.
3. Calculate the Appropriate Depth:
- The refractive index of water (μw) is given as 43.
- The appropriate depth (d) can be calculated using the formula:
Appropriate Depth=Real Depthμw
- Substituting the values:
d=10cm43=10cm×34=7.5cm
Hint: The appropriate depth accounts for the effect of the medium (water) on the light rays, which causes them to appear closer to the surface than they actually are.
4. Determine the Distance of the Image from the Surface of Water:
- The distance of the image from the surface of the water is equal to the appropriate depth calculated above. Thus, the image of the sun is formed at a distance of:
Distance of Image from Water Surface=7.5cm
Hint: The image distance is measured from the surface of the water to the point where the light rays converge after reflecting off the mirror.
Final Answer:
The distance of the image from the surface of the water is 7.5 cm.
- The radius of curvature (R) of the concave mirror is given as 60 cm.
- The focal length (f) of a concave mirror is given by the formula:
f=R2
- Therefore,
f=60cm2=30cm
- The depth of water in the tank is 20 cm. The distance from the mirror to the surface of the water is the focal length minus the height of the water:
Real Depth=f−Height of Water=30cm−20cm=10cm
- The refractive index of water (μw) is given as 43.
- The appropriate depth (d) can be calculated using the formula:
Appropriate Depth=Real Depthμw
- Substituting the values:
d=10cm43=10cm×34=7.5cm
- The distance of the image from the surface of the water is equal to the appropriate depth calculated above. Thus, the image of the sun is formed at a distance of:
Distance of Image from Water Surface=7.5cm
The distance of the image from the surface of the water is 7.5 cm.
Topper's Solved these Questions
- RAY OPTICS AND WAVE OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS AND WAVE OPTICS EXERCISE - IMPECCABLE
58 Videos
- RAY OPTICS AND WAVE OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS AND WAVE OPTICS EXERCISE - ENABLE
50 Videos
- RAY OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - IN-CHAPTER EXERCISE-J
10 Videos
- REVISION TEST-15 JEE - 2020BOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-15 JEE - 2020EXERCISE - PHYSICS
25 Videos
Similar Questions
A convex mirror has its radius of curvature 20 cm. Find the position of the image of an object placed at a distance of 12 cm from the mirror.

View SolutionA concave mirror having a radius of curvature 40 cm is placed in front of an illuminated point source at a distance of 30 cm from it. Find the location of the image.
View SolutionA plane mirror is fixed at the bottom of a tank containing water. A small object is kept at a height of 24 cm from the bottom and is viewed from a point vertically above it. The distance between the object and the image in the mirror as appears to the person is
View SolutionA concave mirror of radius of curvature h is placed at the bottom of a tank containing a liquid of refractive index μ upto a depth d. An object P is placed at height h above the bottom of the miror. Outside the liquid, an observer O views the object and its image in the mirror. The apparent distance between these two will be
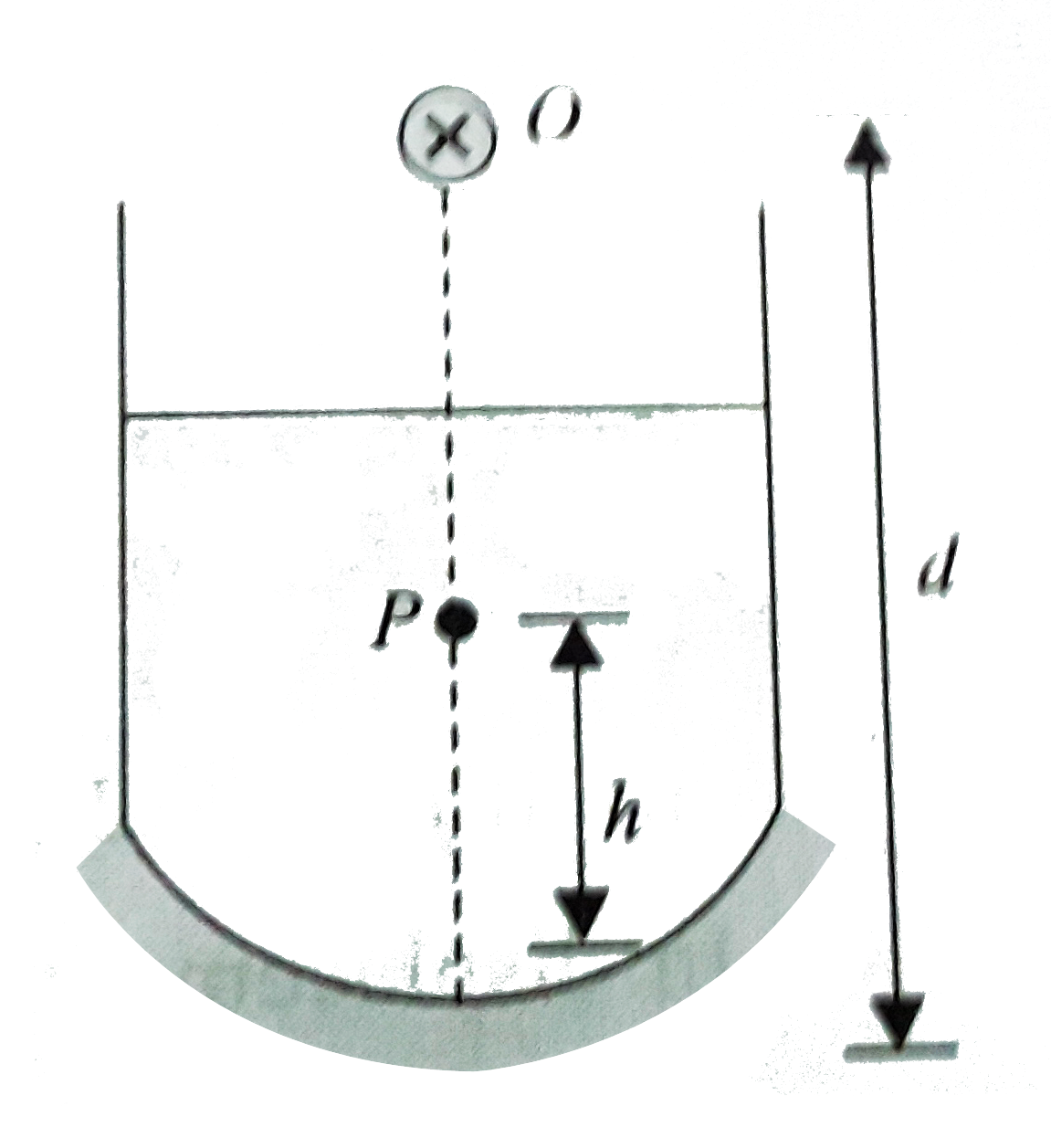
View SolutionA cube with a mass =20g wettable water floats on the surface of water. Each face of the cube is α=3cm long. Surface tension of water is 70dyn/cm. The distance of the lower face of the cube from the surface of water is (g=980cms−12)
View SolutionA concave mirror is placed at the bottom of an empty tank with face upwards and axis vertical. When sunlight falls normally on the mirror, it is focussed at distance of 32cm from the mirror. If the tank filled with water (μ=4/3) up to a height of 20cm, then the sunlight will now get focussed at
View SolutionA point object at 15 cm from a concave mirror of radius of curvature 20 cm is made to oscillate along the principal axis with amplitude 2 mm. The amplitude of its image will be
View SolutionA concave mirror of radius of curvature 40cm forms an image of an object placed on the principal axis at a distance 45 cm in front of it. Now if the system (including object) is completely immersed in water (μ=1.33) , then
View SolutionA concave mirror of focal length 20cm is placed inside water with its shining surface upwards and principla axis vertical as shown in Fig. Rays are incident parallel to the principa, axis of concave mirror. Find the position of final image.

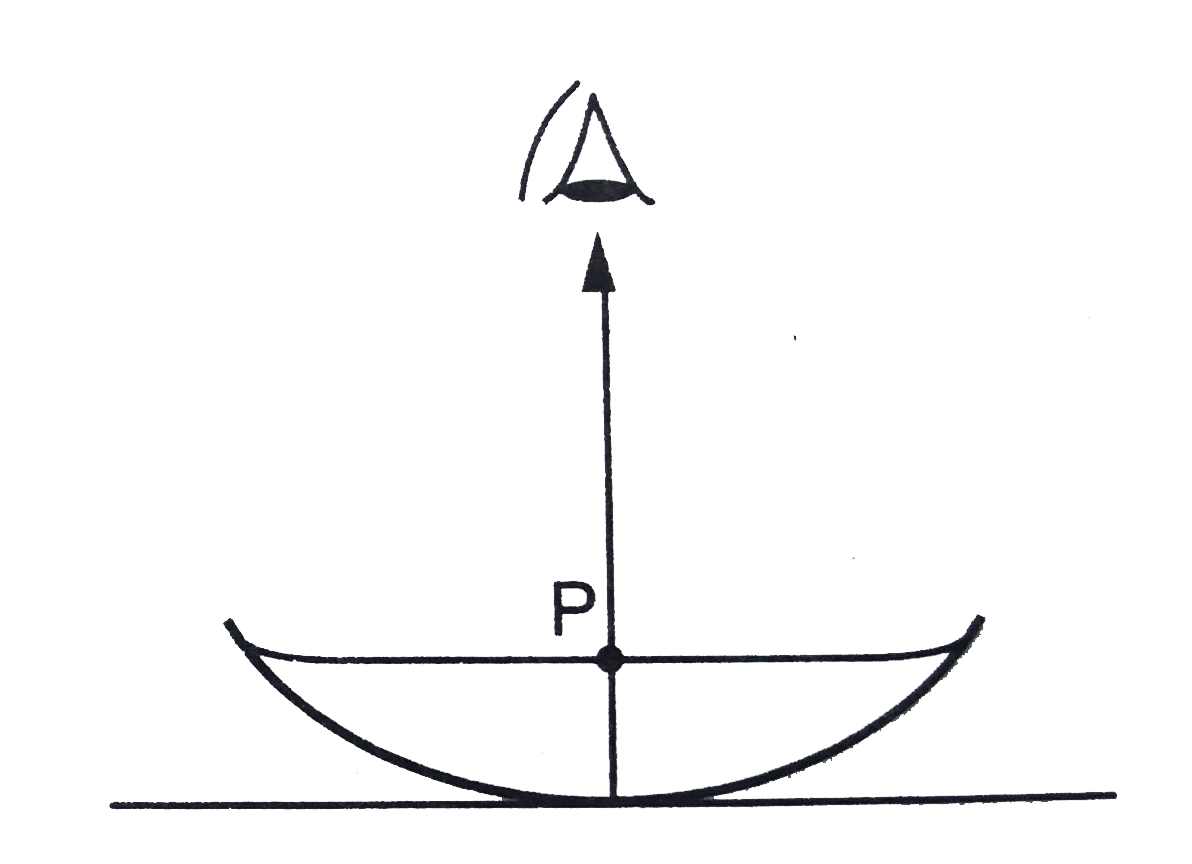
View SolutionA concave mirror of radius 40 cm lies on a horizontal table and water is filled in it upto a height of 5.00 cm. A small dust particle floats on the water surface at a point P vertically above the point of contact of the mirror with the table. Locate the image of the dust particle as seen from a point directly above it. the refractive index of water is 1.33.
View Solution
