A plane mirror is fixed at the bottom of a tank containing water. A small object is kept at a height of 24 cm from the bottom and is viewed from a point vertically above it. The distance between the object and the image in the mirror as appears to the person is
48 cm
64 cm
36 cm
54 cm
The correct Answer is:D
To solve the problem step by step, we need to follow these instructions:
Step 1: Understand the setup
We have a plane mirror fixed at the bottom of a tank filled with water. An object is placed at a height of 24 cm from the bottom of the tank. We need to find the distance between the object and its image as seen from a point directly above the object.
Hint: Visualize the scenario with a diagram to understand the position of the object and the mirror.
Step 2: Identify the height of the object
The height of the object from the bottom of the tank is given as 24 cm.
Hint: Remember that the height is measured from the bottom of the tank to the object.
Step 3: Determine the position of the image
In a plane mirror, the image is formed at the same distance behind the mirror as the object is in front of it. Therefore, if the object is 24 cm above the bottom of the tank, the image will also appear to be 24 cm below the mirror.
Hint: Use the property of plane mirrors that states the distance of the image from the mirror is equal to the distance of the object from the mirror.
Step 4: Calculate the total distance between the object and the image
The total distance between the object and the image can be calculated as follows:
- The distance from the object to the mirror is 24 cm.
- The distance from the mirror to the image is also 24 cm.
Thus, the total distance (D) between the object and the image is:
D=Distance from object to mirror+Distance from mirror to image=24cm+24cm=48cm
Hint: Add the distances from the object to the mirror and from the mirror to the image to find the total distance.
Step 5: Consider the effect of the medium
Since the object is viewed through water, we need to consider the refractive index of water. The effective distance as perceived by the observer is given by the formula:
Effective Distance=Dμ
where D is the distance calculated and μ is the refractive index of water (1.33).
Substituting the values:
Effective Distance=48cm1.33≈36cm
Hint: Remember to divide the total distance by the refractive index to account for the medium through which the image is viewed.
Conclusion
The distance between the object and the image as it appears to the person is approximately 36 cm.
Final Answer: 36 cm
We have a plane mirror fixed at the bottom of a tank filled with water. An object is placed at a height of 24 cm from the bottom of the tank. We need to find the distance between the object and its image as seen from a point directly above the object.
The height of the object from the bottom of the tank is given as 24 cm.
In a plane mirror, the image is formed at the same distance behind the mirror as the object is in front of it. Therefore, if the object is 24 cm above the bottom of the tank, the image will also appear to be 24 cm below the mirror.
The total distance between the object and the image can be calculated as follows:
- The distance from the object to the mirror is 24 cm.
- The distance from the mirror to the image is also 24 cm.
D=Distance from object to mirror+Distance from mirror to image=24cm+24cm=48cm
Since the object is viewed through water, we need to consider the refractive index of water. The effective distance as perceived by the observer is given by the formula:
Effective Distance=Dμ
where D is the distance calculated and μ is the refractive index of water (1.33).
Effective Distance=48cm1.33≈36cm
The distance between the object and the image as it appears to the person is approximately 36 cm.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - PRACTICE SHEET (ADVANCED) (MORE THAN ONE CORRECT TYPE QUESTIOS)
4 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - PRACTICE SHEET (ADVANCED) (LINKED COMPREHENSION CORRECT TYPE QUESTIOS)
7 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE -I (LEVEL-II LECTURE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
4 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
10 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
106 Videos
Similar Questions
An object is at a distance of 0.5m in front of a plane mirror. Distance between the object and image is
View SolutionA plane mirror is placed at the bottom of a tank containing a liquid of refractive index μ. P is a small object at a height h above the mirror. An observer observes P and its image in the mirror. The apparent distance between two will be
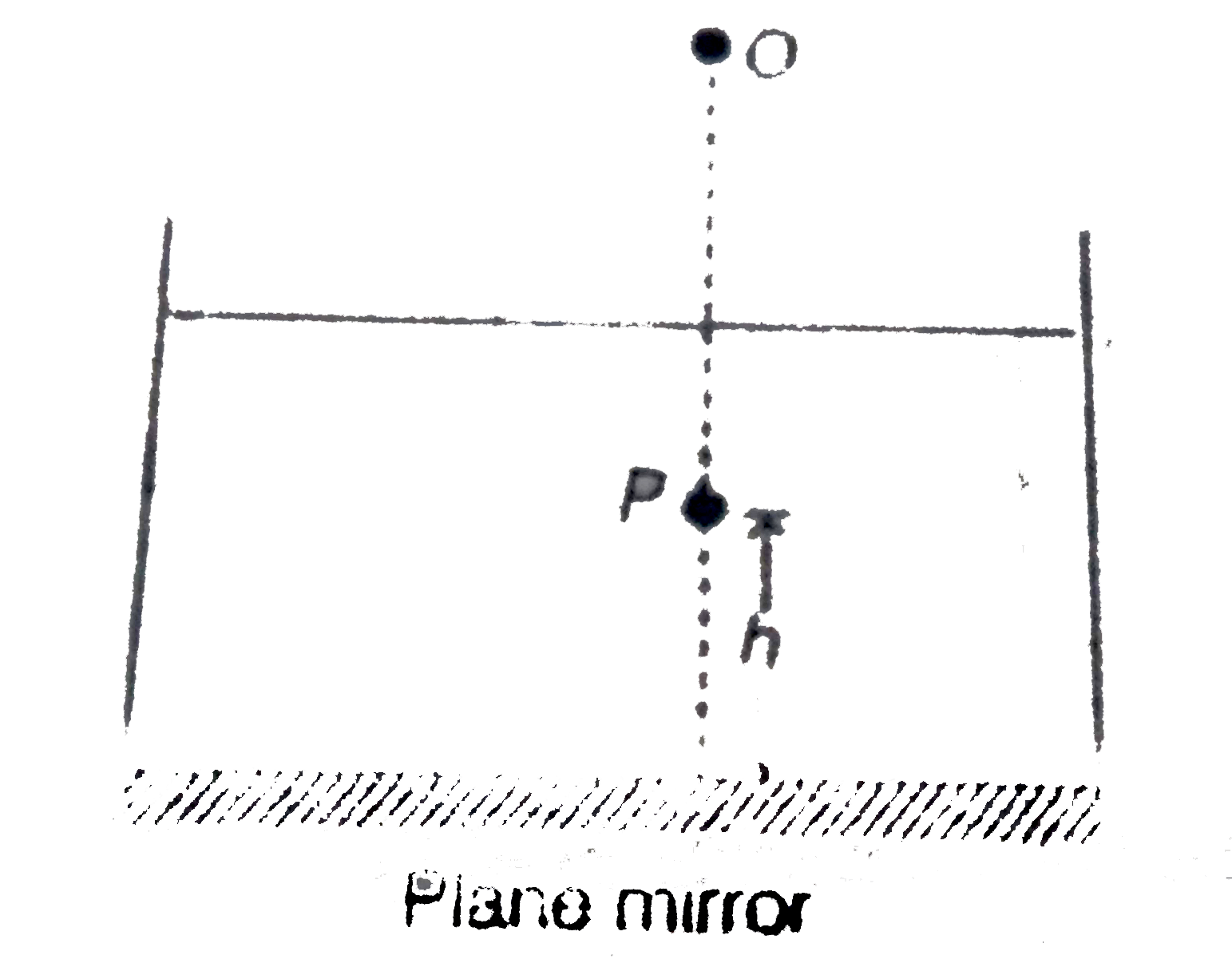
View Solution
Knowledge Check
An object is placed 100 cm from a plane mirror how far is the image from the object?
A50cmB100cmC200cmD300cm
A concave mirror of radius of curvature h is placed at the bottom of a tank containing a liquid of refractive index μ upto a depth d. An object P is placed at height h above the bottom of the miror. Outside the liquid, an observer O views the object and its image in the mirror. The apparent distance between these two will be
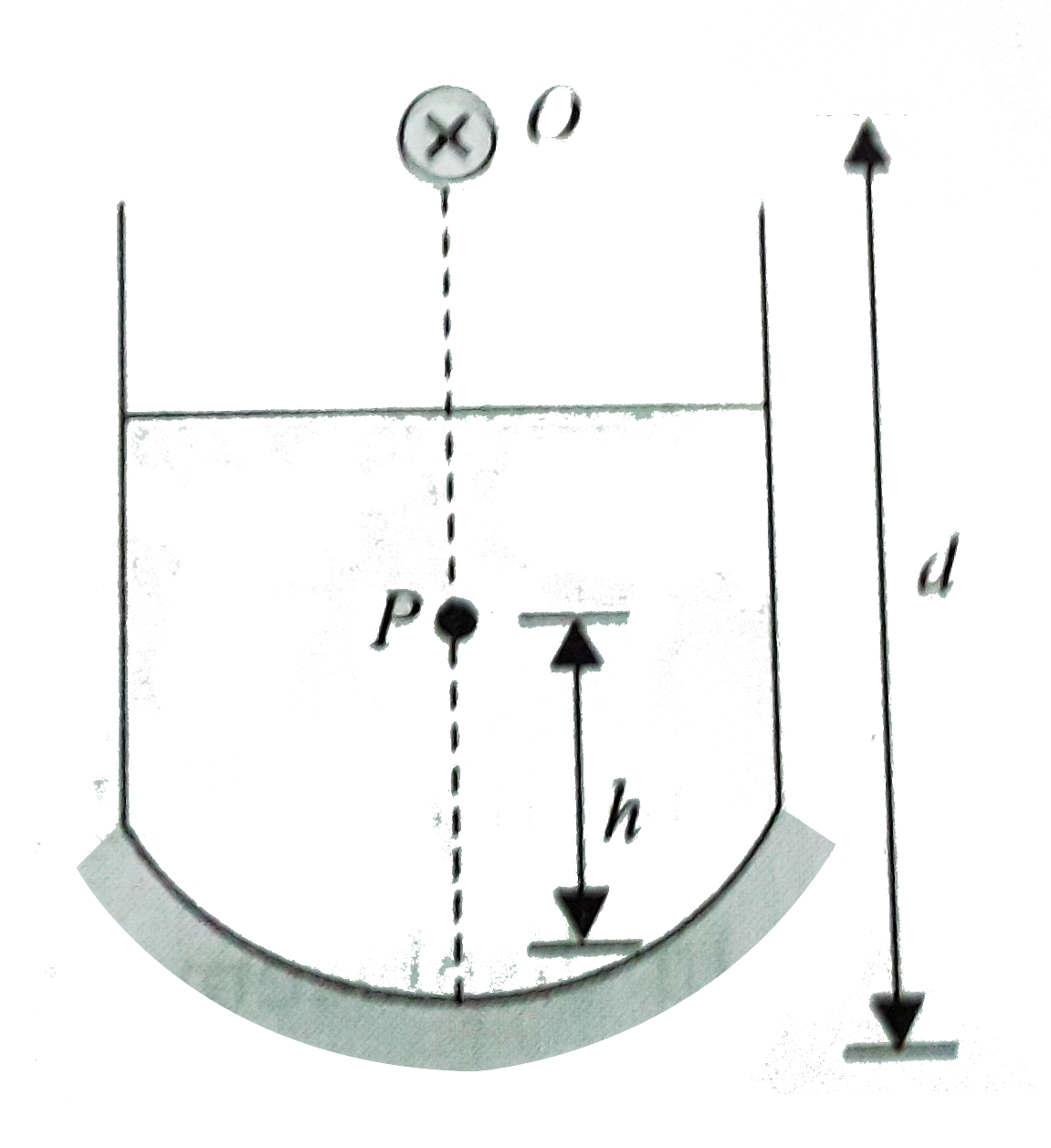
View SolutionA tank contains a transparent liquid of refractive index μ. The bottom of the tank is a plane mirror as shown. A person at P looks at an object O and its image in the mirror. The distance between the object and its image in the mirror as preceived by the person is

View SolutionAn object is placed at a distance of 30 cm from a concave mirror and its real image is formed at a distance of 30 cm from the mirror. The focal length of the mirror is
View SolutionA coin at the bottom of a trough containing water to a depth of 15 cm appears to be 3.75 cm raised above from the bottom. Calculate the refractive index of water.
View SolutionA spherrical mirror forms an erect image three times the size of the object, If the distance between the object and the inage is 80 cm. The nature and the focal length of the mirror are
View SolutionA point object is placed at a distance 20 cm from the focus of a concave mirror of radius of curvature 20 cm. Find the distance (in cm) of the image from the focus.
View SolutionAn object is at a distance 25 cm in front of a plane mirror. The mirror is shifted 5 cm away from the object. Find: (i) the new distance between theobject ad its image, and (ii) the distance between the two positions of the image.
View Solution
