A fcc unit cell of aluminium contains effectively how many atoms?
1
2
3
4
The correct Answer is:D
To determine the number of atoms in a face-centered cubic (FCC) unit cell of aluminum, we can follow these steps:
1. Understand the FCC Structure:
- An FCC unit cell is a cube where atoms are located at each of the eight corners and at the center of each of the six faces.
2. Count the Corner Atoms:
- Each corner atom is shared by eight adjacent unit cells. Therefore, the contribution of one corner atom to the unit cell is 18.
- Since there are 8 corners in a cube, the total contribution from the corner atoms is:
Contribution from corners=8×18=1 atom
3. Count the Face-Centered Atoms:
- Each face-centered atom is shared by two adjacent unit cells. Therefore, the contribution of one face-centered atom to the unit cell is 12.
- Since there are 6 faces in a cube, the total contribution from the face-centered atoms is:
Contribution from faces=6×12=3 atoms
4. Total Number of Atoms in the FCC Unit Cell:
- To find the total number of atoms in the FCC unit cell, we add the contributions from the corner atoms and the face-centered atoms:
Total atoms=Contribution from corners+Contribution from faces=1+3=4 atoms
Final Answer:
The FCC unit cell of aluminum contains effectively 4 atoms.
---
- An FCC unit cell is a cube where atoms are located at each of the eight corners and at the center of each of the six faces.
- Each corner atom is shared by eight adjacent unit cells. Therefore, the contribution of one corner atom to the unit cell is 18.
- Since there are 8 corners in a cube, the total contribution from the corner atoms is:
Contribution from corners=8×18=1 atom
- Each face-centered atom is shared by two adjacent unit cells. Therefore, the contribution of one face-centered atom to the unit cell is 12.
- Since there are 6 faces in a cube, the total contribution from the face-centered atoms is:
Contribution from faces=6×12=3 atoms
- To find the total number of atoms in the FCC unit cell, we add the contributions from the corner atoms and the face-centered atoms:
Total atoms=Contribution from corners+Contribution from faces=1+3=4 atoms
The FCC unit cell of aluminum contains effectively 4 atoms.
Topper's Solved these Questions
- THE SOLID STATEBook:VMC MODULES ENGLISHChapter:THE SOLID STATEExercise:ILLUSTRATIONS
Explore 24 Videos
- THE SOLID STATEBook:VMC MODULES ENGLISHChapter:THE SOLID STATEExercise:EXAMPLE
Explore 20 Videos
- THE SOLID STATEBook:VMC MODULES ENGLISHChapter:THE SOLID STATEExercise:EFFICIENT
Explore 50 Videos
- SURFACE CHEMISTRYBook:VMC MODULES ENGLISHChapter:SURFACE CHEMISTRYExercise:PRACTICE EXERCISE
Explore 9 Videos
- THEORY OF SOLUTIONSBook:VMC MODULES ENGLISHChapter:THEORY OF SOLUTIONSExercise:JEE Advanced (Archive)
Explore 31 Videos
Similar Questions
The unit cell of aluminium is a cube with an edge length of 405 pm. The density of aluminium is 2.70gcm−3 . What type of unit cell of aluminium is ?
View SolutionTungsten has a density of 19.35 g cm−3 and the length of the side of the unit cell is 316 pm. The unit cell is a body centred unit cell. How many atoms does 50 grams of the element contain?
View SolutionThe length of the edge of the face centred cubic unit cell of aluminium is 400 pm. What is the radius of aluminium atom and the nearest neighbour distance ?
View SolutionDensity of a unit cell is respresented as
ρ= Effective no. of atoms (s)×Mass of a unit cell Volume of a unit cell =Z.MNA.a3
where , Z =mass of effective no . of atoms(s) or ion (s).
M= At . mass// formula
NA= Avogadro' s no . ⇒6.0323×1023
a= edge length of unit cell
An element crystallizes in a structure having fcc unit cell of an edge 200 pm . Calculate the density , if 100 g of this element contains 12×1023 atoms :
View SolutionIron occurs as BCC as well as FCC unit cell. If the effective radius of an atom of iron is 124 pm, compute the density of iron in both these structures.
View SolutionDensity of a unit cell is respresented as
ρ= Effective no. of atoms (s)×Mass of a unit cell Volume of a unit cell =Z.MNA.a3
where , Z = effective no . of atoms(s) or ion (s) per unit cell.
M= At . mass// formula
NA= Avogadro' s no . ⇒6.0323×1023
a= edge length of unit cell
Silver crystallizes in a fcc lattice and has a density of 10.6g/cm3. What is the length of a edge of the unit cell ?
View SolutionWhen atoms are placed at the corners of all 12 edges of a cube in a unit cell, how many atoms are present per unit cell? Also name this unit cell.
View SolutionIt was found that in 30unit cells of ZnS, four atoms are of trivalent metal. How many vacant tetrahedral voids are present in 30unit cells of ZnS?
View SolutionIn fcc unit cell, atoms are numbered as shown below.
The atoms not touching each other are (Atom numbered 3 is face centre of front face)

View SolutionIn an fcc unit cell, atoms are numbered as shown below
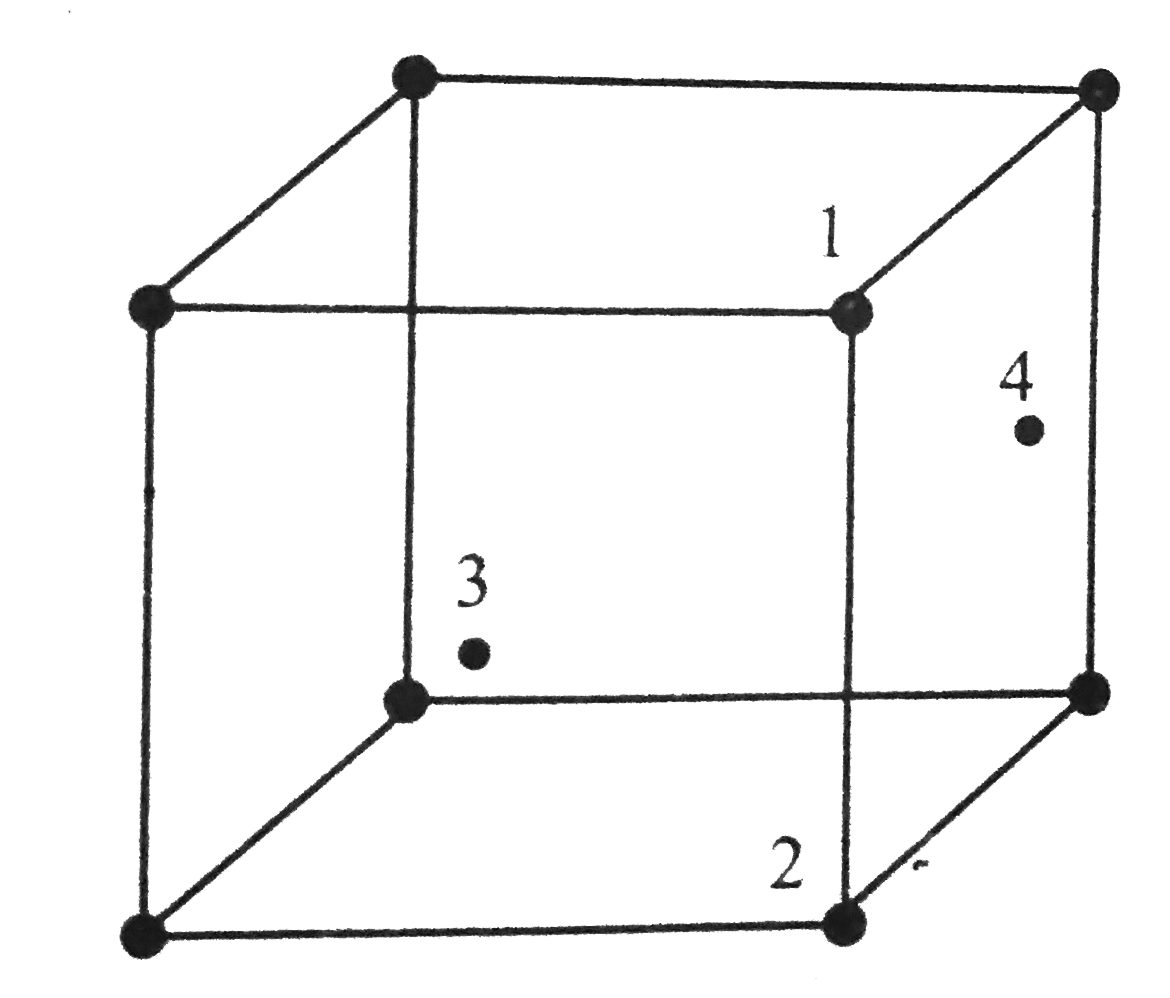
The atoms not touching each other are (Atom numbered 3 is face center of front face)
View Solution
