The wavelengths of photons emitted by electron transition between two similar leveis in H and He+ are λ1 and λ2 respectively. Then :-
λ2=λ12
λ2=λ14
λ2=λ1
λ2=2λ1
The correct Answer is:B
To solve the problem regarding the wavelengths of photons emitted by electron transitions in hydrogen (H) and helium ion (He⁺), we can follow these steps:
1. Understand the Energy Transition:
The energy of the photon emitted during an electron transition from a higher energy level (n2) to a lower energy level (n1) can be expressed as:
ΔE=hcλ
where h is Planck's constant, c is the speed of light, and λ is the wavelength of the emitted photon.
2. Apply the Formula for Hydrogen:
For hydrogen (where the atomic number Z=1), the energy difference for the transition can be written as:
ΔEH=hcλ1
3. Apply the Formula for Helium Ion (He⁺):
For helium ion (where the atomic number Z=2), the energy difference for the transition can be expressed as:
ΔEHe+=hcλ2=Z2⋅ΔEH=4⋅ΔEH
Therefore, we can write:
hcλ2=4⋅hcλ1
4. Cancel out Common Terms:
Since hc appears in both equations, we can cancel it out:
1λ2=4⋅1λ1
5. Rearranging the Equation:
Rearranging gives us:
λ2=λ14
6. Conclusion:
This means that the wavelength of the photon emitted by the transition in helium ion is one-fourth the wavelength of the photon emitted in hydrogen:
λ2=14λ1
Final Answer:
Thus, the relationship between the wavelengths is:
λ2=14λ1
The energy of the photon emitted during an electron transition from a higher energy level (n2) to a lower energy level (n1) can be expressed as:
ΔE=hcλ
where h is Planck's constant, c is the speed of light, and λ is the wavelength of the emitted photon.
For hydrogen (where the atomic number Z=1), the energy difference for the transition can be written as:
ΔEH=hcλ1
For helium ion (where the atomic number Z=2), the energy difference for the transition can be expressed as:
ΔEHe+=hcλ2=Z2⋅ΔEH=4⋅ΔEH
Therefore, we can write:
hcλ2=4⋅hcλ1
Since hc appears in both equations, we can cancel it out:
1λ2=4⋅1λ1
Rearranging gives us:
λ2=λ14
This means that the wavelength of the photon emitted by the transition in helium ion is one-fourth the wavelength of the photon emitted in hydrogen:
λ2=14λ1
Thus, the relationship between the wavelengths is:
λ2=14λ1
Topper's Solved these Questions
- STRUCTURE OF ATOMBOOK - VMC MODULES ENGLISHCHAPTER - STRUCTURE OF ATOMEXERCISE - EFFICIENT
48 Videos
- STRUCTURE OF ATOMBOOK - VMC MODULES ENGLISHCHAPTER - STRUCTURE OF ATOMEXERCISE - IMPECCABLE
49 Videos
- STRUCTURE OF ATOMBOOK - VMC MODULES ENGLISHCHAPTER - STRUCTURE OF ATOMEXERCISE - IN-CHAPTER EXERCISE-F
7 Videos
- STOICHIOMETRY-IIBOOK - VMC MODULES ENGLISHCHAPTER - STOICHIOMETRY-IIEXERCISE - JEE Advanced (Archive)
43 Videos
- SURFACE CHEMISTRYBOOK - VMC MODULES ENGLISHCHAPTER - SURFACE CHEMISTRYEXERCISE - PRACTICE EXERCISE
9 Videos
Similar Questions
A dye absorbs a photon of wavelength λ and re− emits the same energy into two phorons of wavelengths λ1 and λ2 respectively. The wavelength λ is related with λ1 and λ2 as :
View SolutionThe wavelengths and frequencies of photons in transition 1,2 and 3 for hydrogen like atom are λ1,λ2,λ3,v1,v2 and v3 respectively. Then:

View Solution
Knowledge Check
The energies E1andE2 of two radiations are 25 eV and 50 eV respectively. The relation between their wavelengths, i.e., λ1andλ2 will be
Aλ1=2λ2Bλ1=4λ2Cλ1=12Dλ1=λ2
Calculate the wavelength of a photon emitted when an electron in H− atom maker a transition from n=2 to n=1
View SolutionThe wavelength of the short radio waves, microwaves, ultraviolet waves are λ1,λ2 and λ3, respectively, Arrange them in decreasing order.
View SolutionIn a set of experiment on a hydrogen on a hypotherical one-electron atom, the wavelength of the photons emitted from transition ending in the ground state (n=1) are shown in the energy level diagram
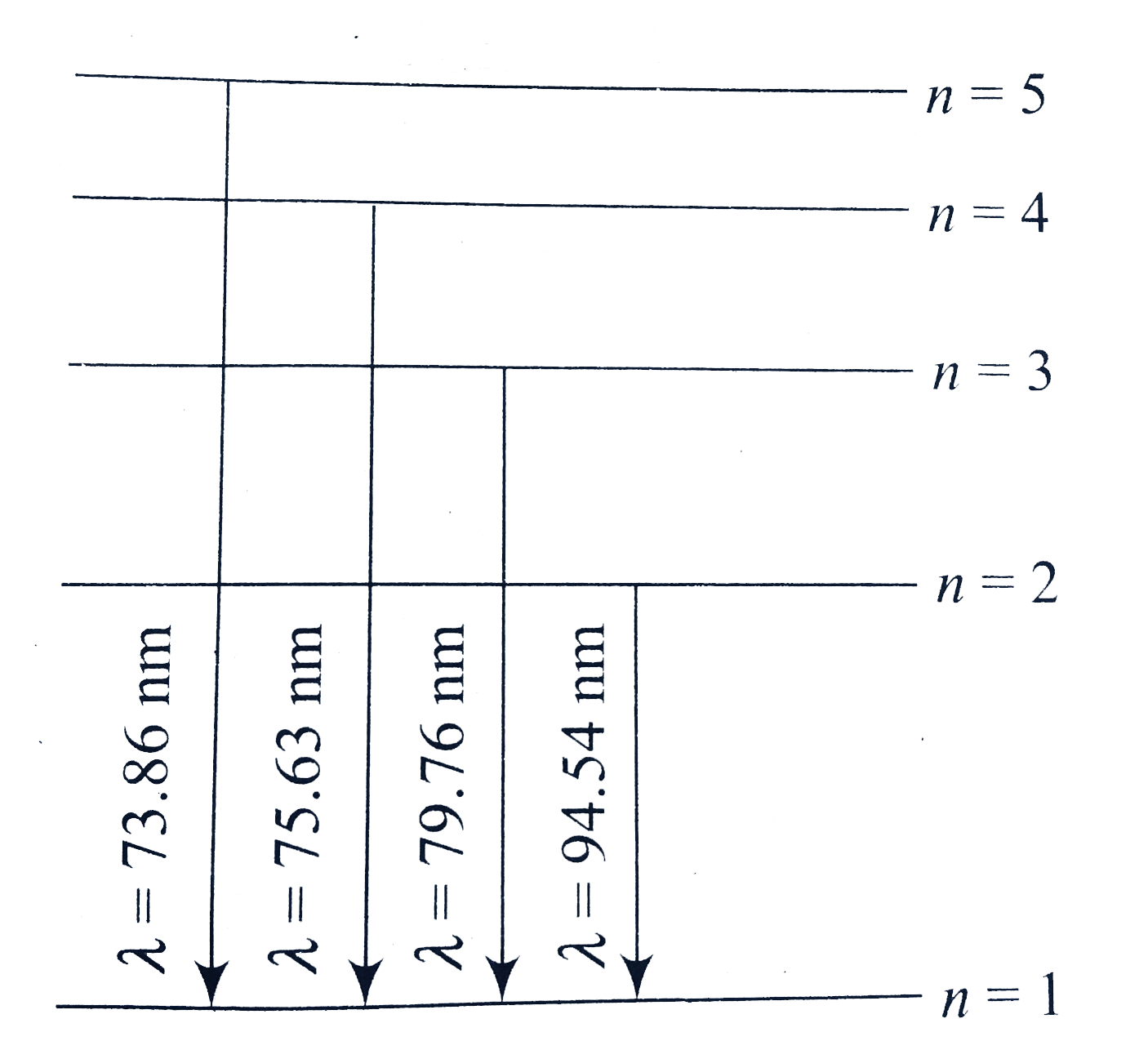
λ5→1=73.86nm
λ4→1=75.63nm
λ3→1=79.76nm
λ2→1=94.54nm
If an electron made a transition from n = 4 to n = 2 level, the wavelength of the light that it would emit is nearly
View SolutionIn a set of experiment on a hydrogen on a hypotherical one-electron atom, the wavelength of the photons emitted from transition ending in the ground state (n=1) are shown in the energy level diagram
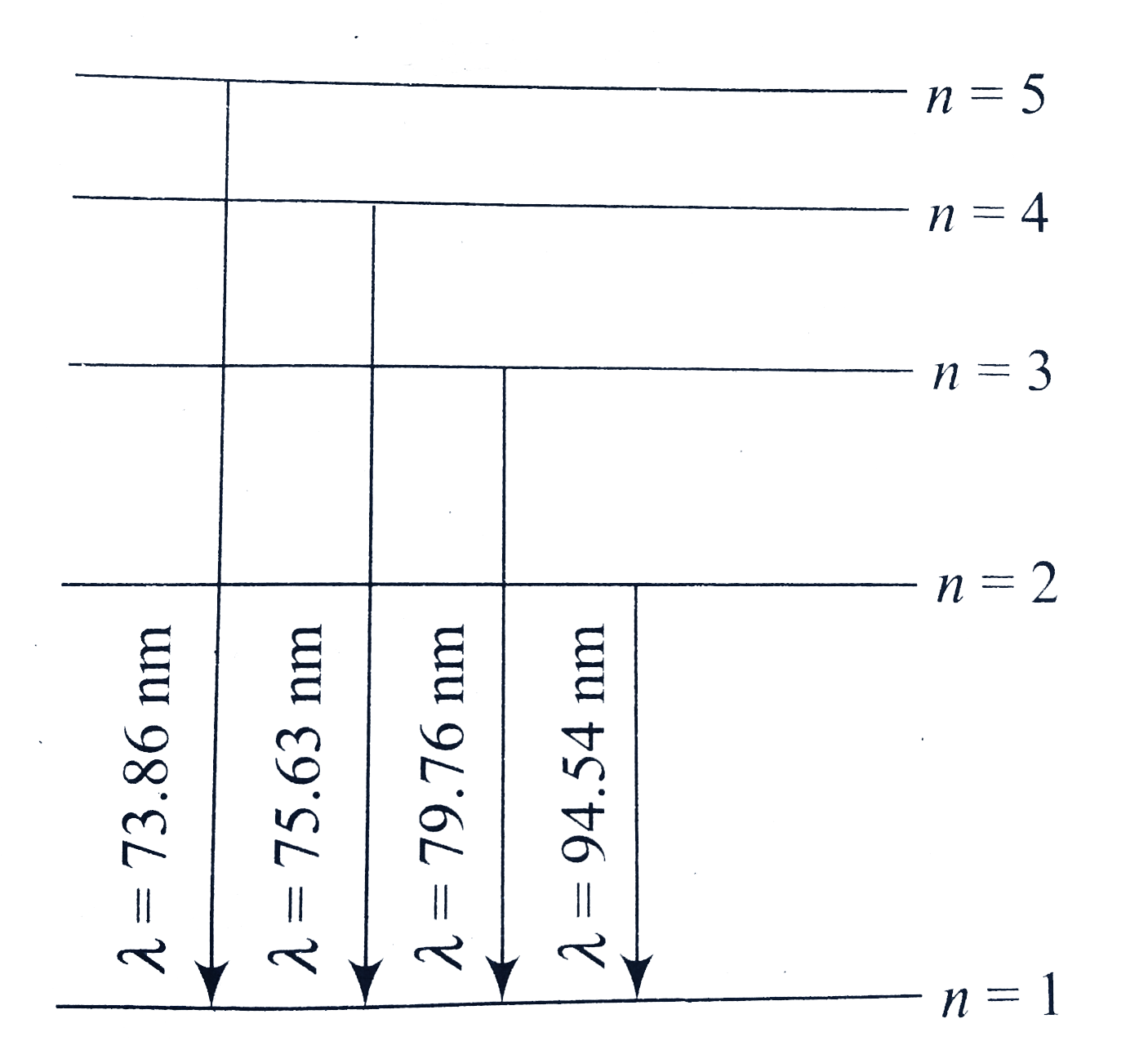
λ5→1=73.86nm
λ4→1=75.63nm
λ3→1=79.76nm
λ2→1=94.54nm
The energy of the atom in level n=1 is nearly
View SolutionIn a set of experiment on a hydrogen on a hypotherical one-electron atom, the wavelength of the photons emitted from transition ending in the ground state (n=1) are shown in the energy level diagram
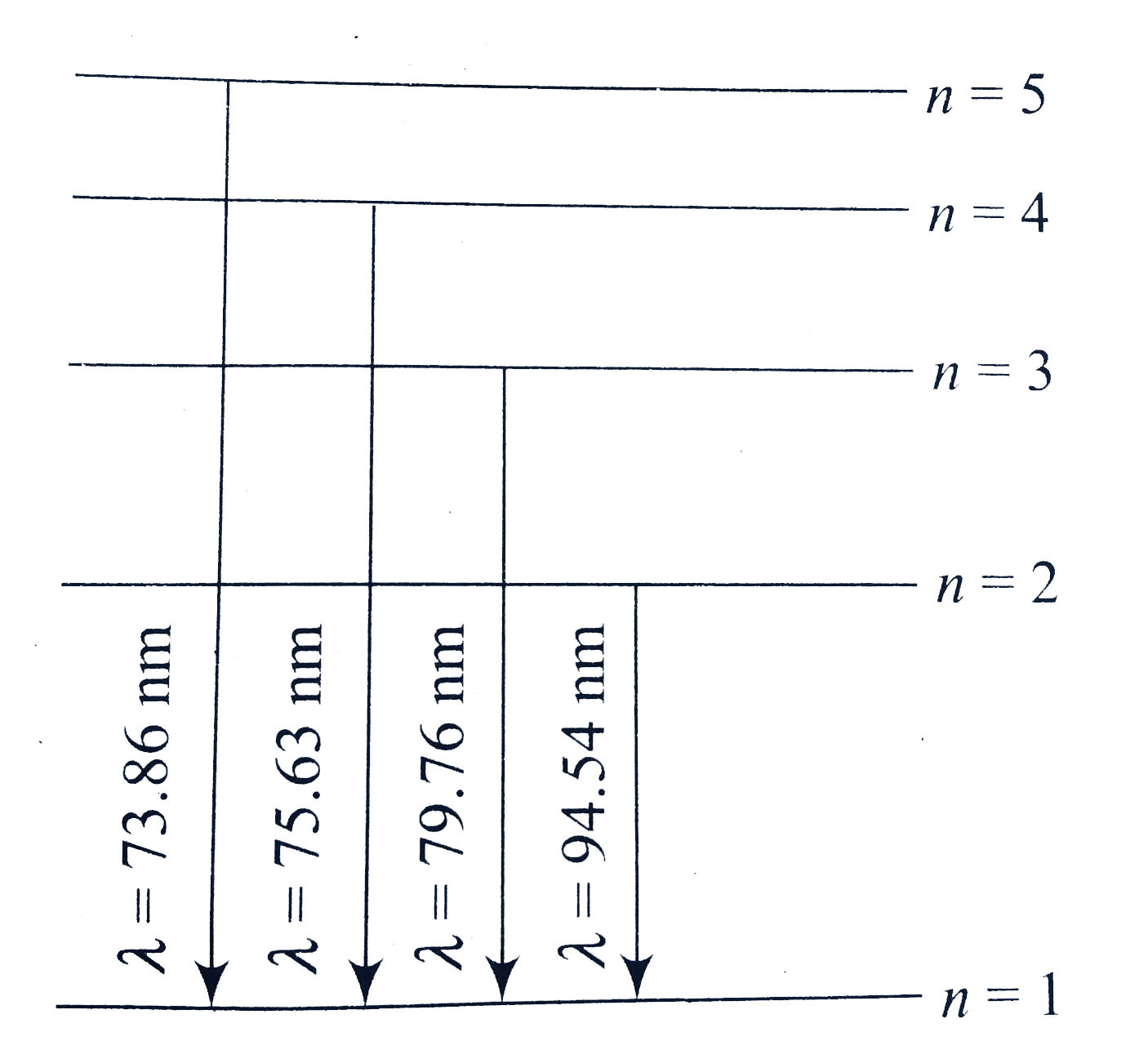
λ5→1=73.86nm
λ4→1=75.63nm
λ3→1=79.76nm
λ2→1=94.54nm
The possible energy of the atom in n=3 cannot be
View SolutionIf the wavelength of photon emitted due to transition of electron from third orbit to first orbit in a hydrogen atom is λ then the wavelength of photon emitted due to transition of electron from fourth orbit to second orbit will be
View SolutionStatement I : The energy of a He+ ion for a given n is almost exactly four times that of H atom for the same n.
Statement II : Photon emitted during transition between corresponds pair of levels in He+ and H have the same energy E and the same wavelength λ=hc/E.
View Solution
