What will be the expression for the differential form of Boyle’s law?
To derive the differential form of Boyle's Law, we start with the basic understanding of Boyle's Law itself. Boyle's Law states that the pressure (P) of a gas is inversely proportional to its volume (V) when the temperature is held constant. Mathematically, this can be expressed as:
P∝1V
This can also be written as:
PV=k
where k is a constant at a given temperature.
Step 1: Differentiate the equation
To find the differential form, we need to differentiate the equation PV=k with respect to volume (V).
Using the product rule of differentiation, we have:
d(PV)=d(k)
Since k is a constant, d(k)=0. Therefore, we can write:
PdV+VdP=0
Step 2: Rearranging the equation
Now, we can rearrange the equation to express dP in terms of dV:
VdP=−PdV
Dividing both sides by V:
dP=−PVdV
Step 3: Expressing in terms of a constant
We can introduce a constant k to represent the relationship between pressure and volume. Thus, we can write:
dP=−kdV
where k=PV.
Step 4: Relating to the square of volume
To express this in terms of volume squared, we can relate k to the volume:
dP=−kV2dV
This gives us the final expression for the differential form of Boyle's Law:
dPdV=−kV2
Final Expression
Thus, the expression for the differential form of Boyle’s Law is:
dPdV=−PV2
---
To find the differential form, we need to differentiate the equation PV=k with respect to volume (V).
Now, we can rearrange the equation to express dP in terms of dV:
We can introduce a constant k to represent the relationship between pressure and volume. Thus, we can write:
To express this in terms of volume squared, we can relate k to the volume:
Thus, the expression for the differential form of Boyle’s Law is:
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - STATES OF MATTEREXERCISE - PRACTICE EXERCISE-34videos
STATES OF MATTER
- BOOK - VMC MODULES ENGLISHCHAPTER - STATES OF MATTEREXERCISE - PRACTICE EXERCISE-42videos
STATES OF MATTER
- BOOK - VMC MODULES ENGLISHCHAPTER - STATES OF MATTEREXERCISE - PRACTICE EXERCISE-13videos
STATES OF MATTER
- BOOK - VMC MODULES ENGLISHCHAPTER - STATES OF MATTEREXERCISE - IMPECCABLE50videos
STATES OF MATTER
- BOOK - VMC MODULES ENGLISHCHAPTER - STOICHIOMETRY - IEXERCISE - JEE Advanced (Archive)31videos
STOICHIOMETRY - I
Similar Questions
Knowledge Check
- Question 1 - Select One
Boyle.s Law is
AP1V1=P2V2BP2V1=P1V2CV1T1=V2T2DV1T1=V2T2 - Question 2 - Select One
Which of the following is according to Boyle's law?
A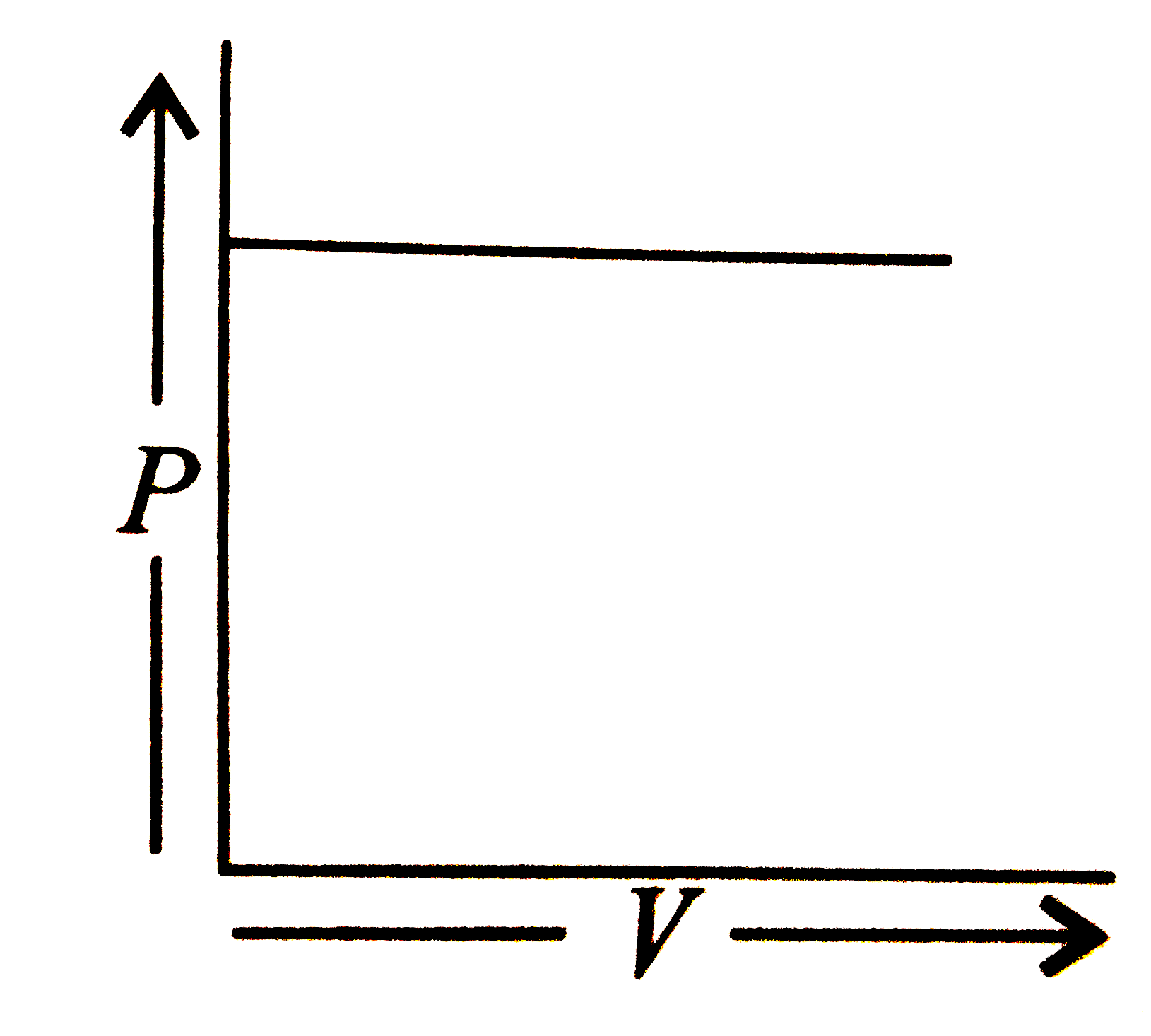 B
B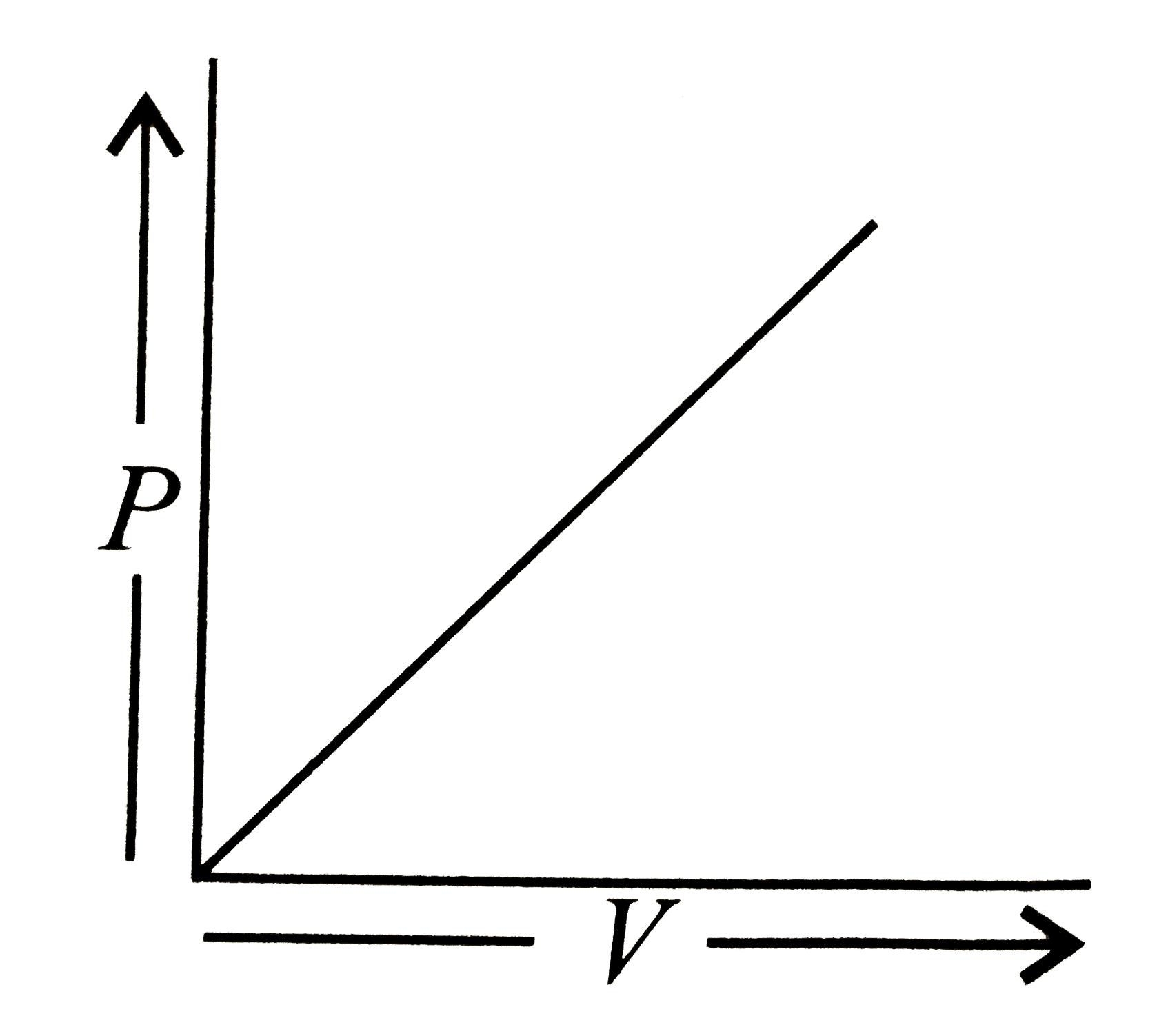 C
C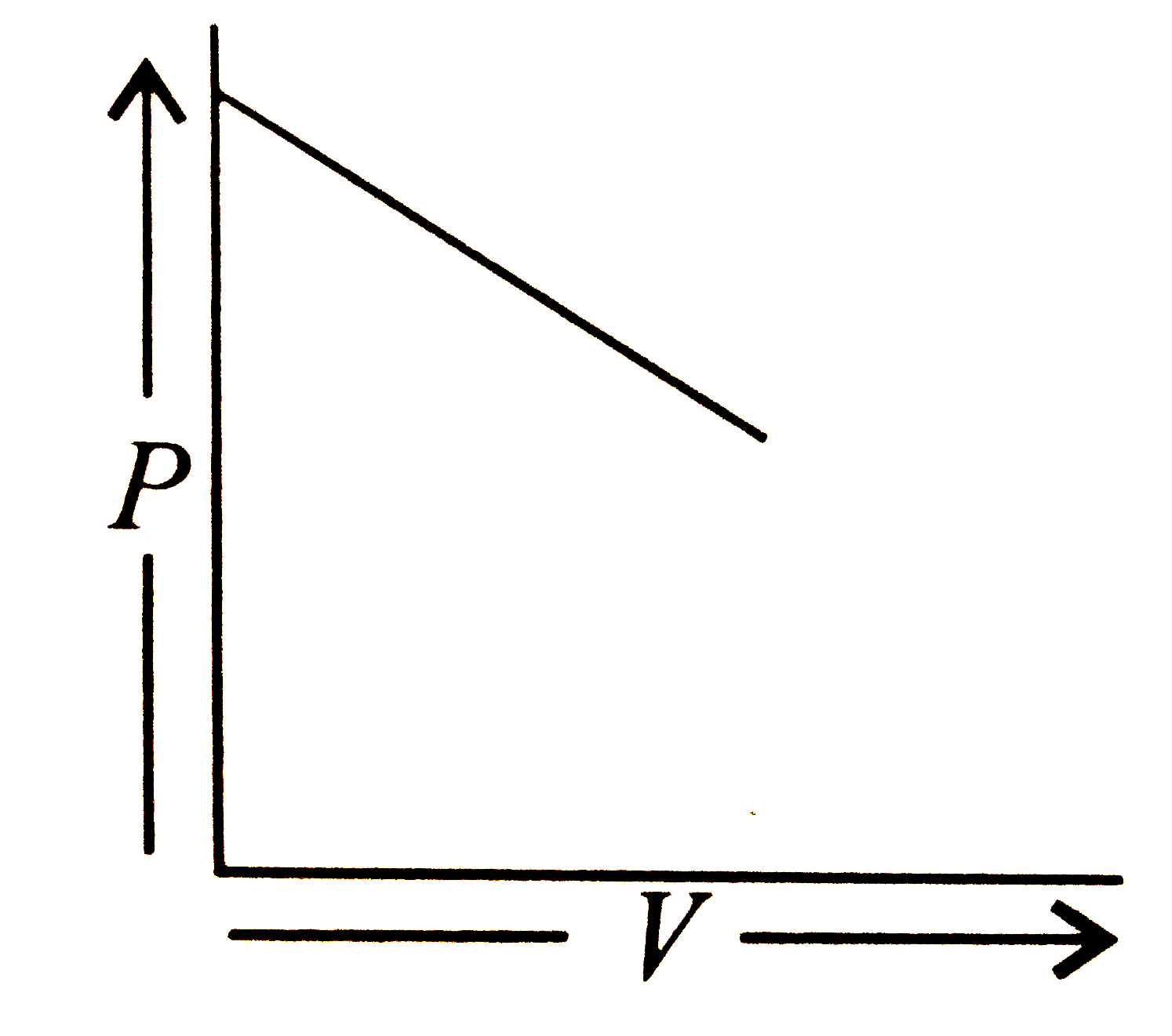 D
D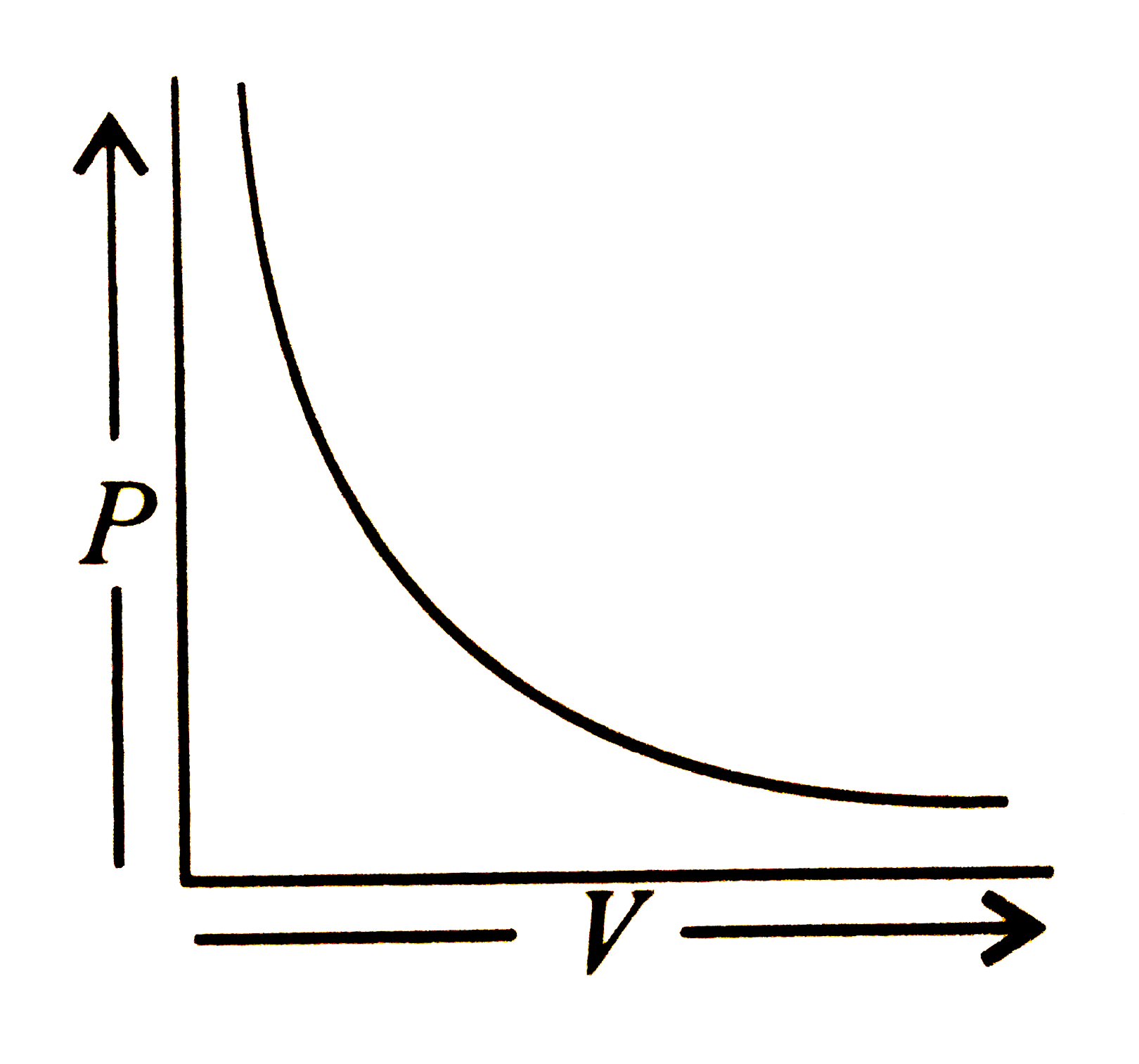
The correct differential from of Newtons second law is
View SolutionWhy do real gases deviate from Boyle's law?
View SolutionGive the significanceof Boyle.s law
View SolutionGive the mathematical expression of Boyle.s law.
View SolutionState Boyle.s Law.
View SolutionWhich of the following is/are true for Boyle's law?
View Solution

