What is the type of graph between log P and log V at constant temperature?
To determine the type of graph between log P (logarithm of pressure) and log V (logarithm of volume) at constant temperature, we can follow these steps:
1. Start with the Ideal Gas Equation:
The ideal gas equation is given by:
PV=nRT
where P is the pressure, V is the volume, n is the number of moles of gas, R is the universal gas constant, and T is the absolute temperature.
2. Consider Constant Temperature:
At constant temperature, the product nRT is a constant. Therefore, we can express this as:
PV=k
where k=nRT is a constant.
3. Express Pressure in Terms of Volume:
Rearranging the equation gives us:
P=kV
This shows that pressure is inversely proportional to volume at constant temperature.
4. Take the Logarithm of Both Sides:
Taking the logarithm of both sides of the equation PV=k:
log(PV)=log(k)
This can be expanded using logarithmic properties:
logP+logV=logk
5. Rearrange the Equation:
Rearranging gives:
logP=−logV+logk
This equation is in the form of a straight line y=mx+c, where:
- y=logP
- x=logV
- The slope m=−1
- The y-intercept c=logk
6. Conclusion:
The graph of log P versus log V at constant temperature is a straight line with a negative slope of -1 and an intercept of log k.
Final Answer:
The type of graph between log P and log V at constant temperature is a straight line with a slope of -1.
---
The ideal gas equation is given by:
PV=nRT
where P is the pressure, V is the volume, n is the number of moles of gas, R is the universal gas constant, and T is the absolute temperature.
At constant temperature, the product nRT is a constant. Therefore, we can express this as:
PV=k
where k=nRT is a constant.
Rearranging the equation gives us:
P=kV
This shows that pressure is inversely proportional to volume at constant temperature.
Taking the logarithm of both sides of the equation PV=k:
log(PV)=log(k)
This can be expanded using logarithmic properties:
logP+logV=logk
Rearranging gives:
logP=−logV+logk
This equation is in the form of a straight line y=mx+c, where:
- y=logP
- x=logV
- The slope m=−1
- The y-intercept c=logk
The graph of log P versus log V at constant temperature is a straight line with a negative slope of -1 and an intercept of log k.
The type of graph between log P and log V at constant temperature is a straight line with a slope of -1.
Topper's Solved these Questions
- STATES OF MATTERBook:VMC MODULES ENGLISHChapter:STATES OF MATTERExercise:PRACTICE EXERCISE-3
Explore 4 Videos
- STATES OF MATTERBook:VMC MODULES ENGLISHChapter:STATES OF MATTERExercise:PRACTICE EXERCISE-4
Explore 2 Videos
- STATES OF MATTERBook:VMC MODULES ENGLISHChapter:STATES OF MATTERExercise:PRACTICE EXERCISE-1
Explore 3 Videos
- STATES OF MATTERBook:VMC MODULES ENGLISHChapter:STATES OF MATTERExercise:IMPECCABLE
Explore 50 Videos
- STOICHIOMETRY - IBook:VMC MODULES ENGLISHChapter:STOICHIOMETRY - IExercise:JEE Advanced (Archive)
Explore 31 Videos
Similar Questions
What is the type of graph between log P and log(1V) at constant temperature for a given amount of gas ?
View SolutionThe slope of the graph between log P and log V at constant temperature for a given mass of gas is
View SolutionThe graph betwene P and V at constant temperature should look like
View SolutionWhat is the type of graph that would result between log(V) and log(T) at constant pressure?
View SolutionThe graph between log t1/2 and log a at a given temperature is
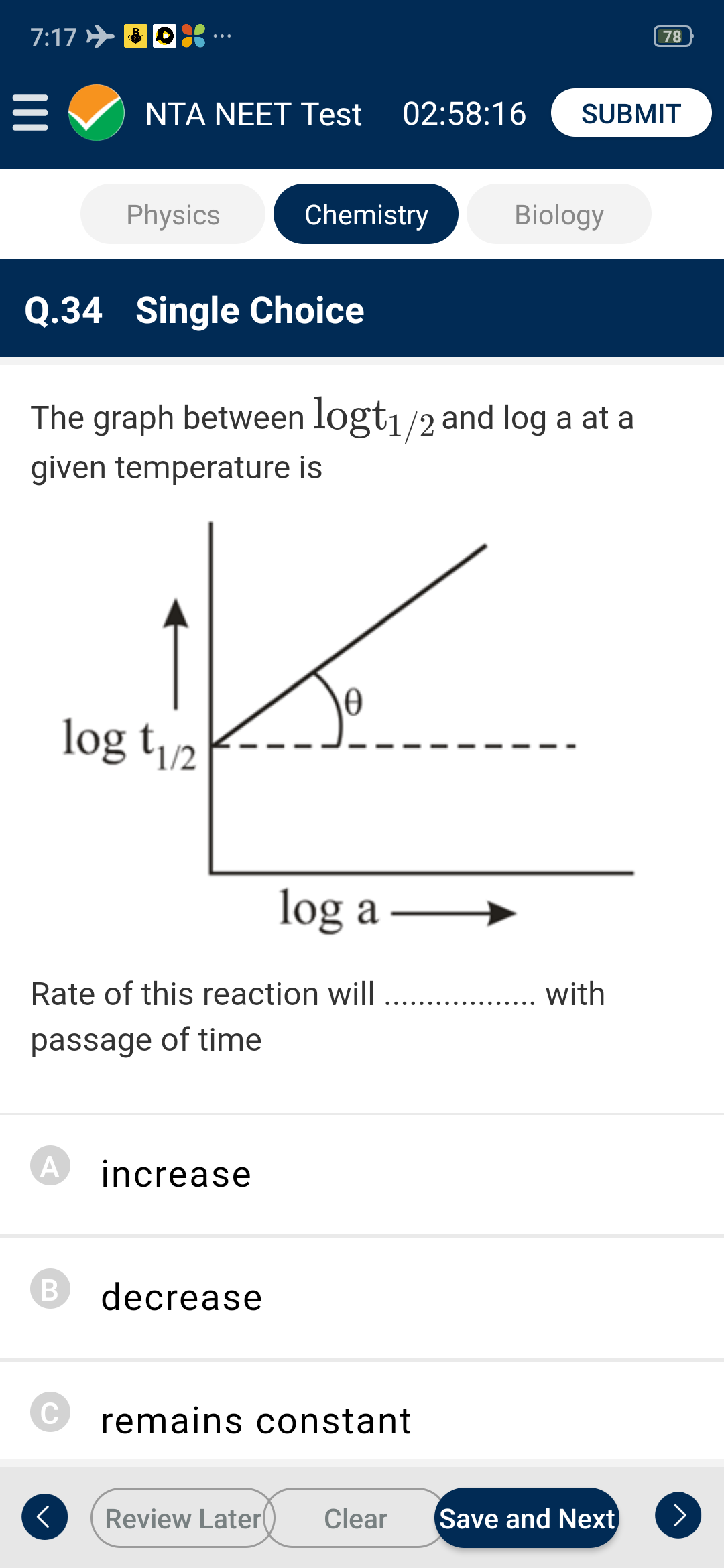
Rate of this reaction will …….with passage of time
View SolutionFor a given mass of a gas what is the shape of (p) versus (1V) graph at constant temperature ?
View SolutionFollowing is the graph between logT50 and loga (a= initial concentration) for a given reaction at 27∘C. Hence order is

View SolutionFollowing is the graph between logt1/2 and loga (a initial concentration) for a given reaction at 300K

Find the order of reaction.
View SolutionAt constant temperature if a graph plotted between logP and log(1V) has an intercept of unity then what will be the value of constant (k)
View SolutionGraph between speed v of sound in air and pressure P at a constant temperature is given by
View Solution