Any series of operations so carried out that at the end, the system is back to its initial state is called
Boyle's cycle
Reversible process
Adiabatic process
Cyclic process
The correct Answer is:D
To solve the question, we need to identify the term that describes a series of operations where the system returns to its initial state. Here’s the step-by-step solution:
Step 1: Understand the Concept
The question asks about a series of operations that lead a system back to its initial state. This concept is fundamental in thermodynamics and relates to how systems behave under various processes.
Hint: Think about processes in thermodynamics where the starting and ending conditions are the same.
Step 2: Identify the Type of Process
In thermodynamics, there are various types of processes (isothermal, adiabatic, etc.), but the specific type that fits the description of returning to the initial state is known as a cyclic process.
Hint: Recall the definition of a cyclic process in thermodynamics. What happens to the system's state variables?
Step 3: Define Cyclic Process
A cyclic process is defined as a series of thermodynamic operations where the system undergoes changes but eventually returns to its original state. This means that all state variables (like pressure, volume, and temperature) are the same at the beginning and end of the process.
Hint: Consider how a cyclic process can be represented graphically, such as on a PV diagram.
Step 4: Example of a Cyclic Process
An example of a cyclic process can be illustrated on a Pressure-Volume (PV) diagram. If a system moves through points A, B, C, and D and returns to point A, it demonstrates a cyclic process.
Hint: Visualize a loop on a graph that starts and ends at the same point.
Final Answer
Therefore, any series of operations so carried out that at the end, the system is back to its initial state is called a cyclic process.
The question asks about a series of operations that lead a system back to its initial state. This concept is fundamental in thermodynamics and relates to how systems behave under various processes.
In thermodynamics, there are various types of processes (isothermal, adiabatic, etc.), but the specific type that fits the description of returning to the initial state is known as a cyclic process.
A cyclic process is defined as a series of thermodynamic operations where the system undergoes changes but eventually returns to its original state. This means that all state variables (like pressure, volume, and temperature) are the same at the beginning and end of the process.
An example of a cyclic process can be illustrated on a Pressure-Volume (PV) diagram. If a system moves through points A, B, C, and D and returns to point A, it demonstrates a cyclic process.
Therefore, any series of operations so carried out that at the end, the system is back to its initial state is called a cyclic process.
Topper's Solved these Questions
- CHEMICAL THERMODYNAMICS BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL THERMODYNAMICS EXERCISE - IN - CHAPTER EXERCISE - B
10 Videos
- CHEMICAL THERMODYNAMICS BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL THERMODYNAMICS EXERCISE - IN - CHAPTER EXERCISE - C
10 Videos
- CHEMICAL THERMODYNAMICS BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL THERMODYNAMICS EXERCISE - PRACTICE EXERCISE
22 Videos
- CHEMICAL KINETICS BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL KINETICS EXERCISE - JEE Advanced (Archive)
52 Videos
- CLASSIFICATION OF ELEMENTS AND PERIODICITY IN PROPERTIES BOOK - VMC MODULES ENGLISHCHAPTER - CLASSIFICATION OF ELEMENTS AND PERIODICITY IN PROPERTIES EXERCISE - JEE ADVANCE (ARCHIVE)
30 Videos
Similar Questions
A closed system receives 200kJ of heat at constant volume. It then rejects 100kJ of heat while it has 50kJ of work done on it at constant pressure. If an adiabatic process can be found which will restore the system to its initial state, the work done by the system during this process is
View SolutionA gas undergoes a change of state during which 100J of heat is supplied to it and it does 20J of work. The system is brough back to its original state through a process during which 20 J of heat is released by the gas. What is the work done by the gas in the second process?
View SolutionIdentify the logic operation carried out by the following circuit

View SolutionTransportation in plants is carried out by a …………...system.
View SolutionYou are given a circuit below. Write its truth table. Hence, identify the logic operation carried out by this circuit. Draw the logic symbol of the gate it corresponds to.
View Solution
You are given a circuit below. Write its truth table. Hence, identify the logic operation carried out by this circuit. Draw the logic symbol of the gate it corresponds to.
View SolutionSix grams of hydrogen gas at a temperature of 273 K isothoermally expanded to five times its initial volume and then isochorically heated so that the pressure in the final state becomes equal to that in the initial state. Find the total amount of heat absorbed by the gas during the entire process.
View SolutionWhat is the equation of state of an ideal gas ? Why is it so called ?
View SolutionWhat is the ratio of displacement to the path length traversed by an object, if the object comes back to its initial position?
View SolutionIn the figure given two processes AandB are shown by which a thermodynamic system goes from initial state I to final state F. if ΔQA and ΔQB are respectively the heats supplied to the systems then
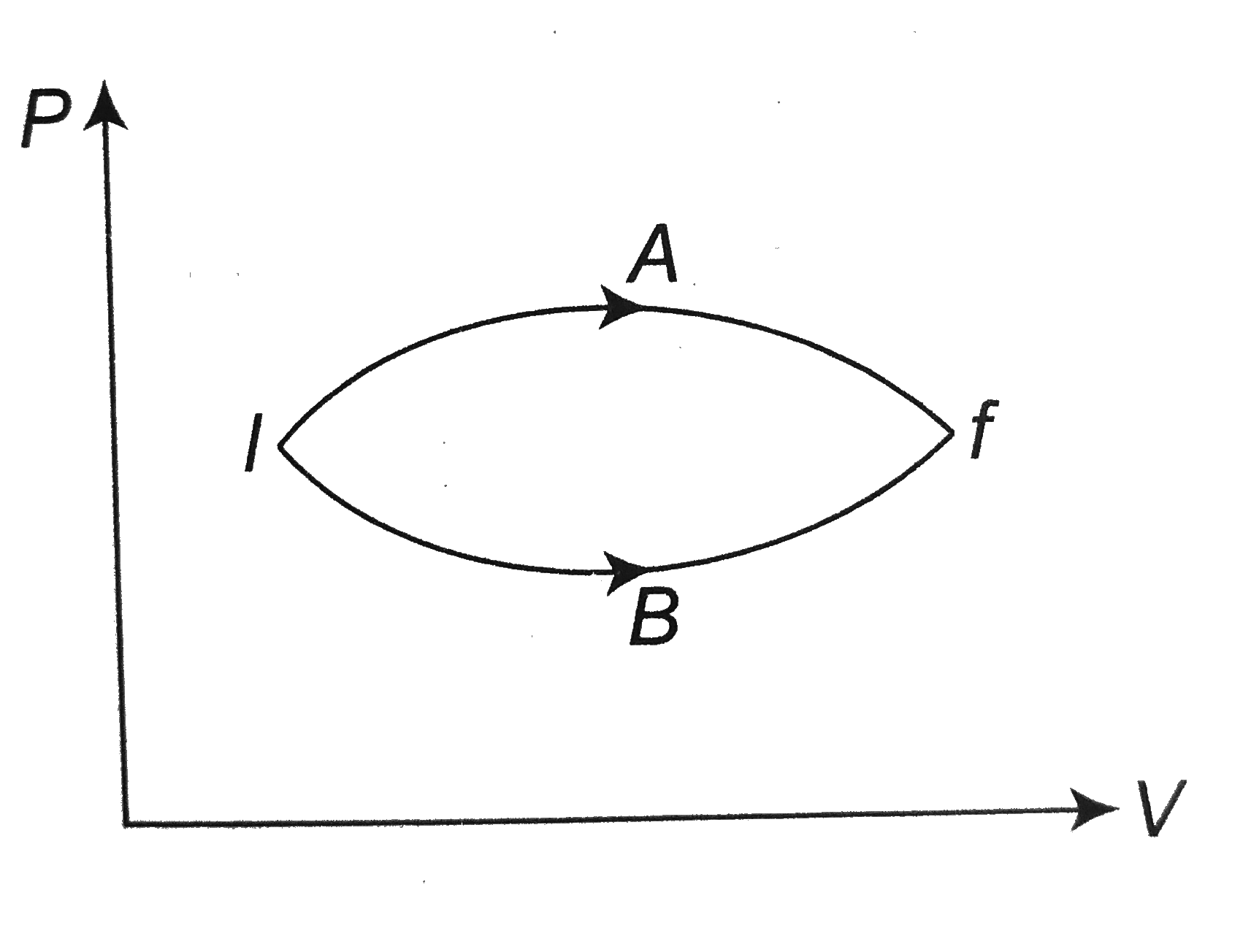
View Solution
