A gas undergoes a change of state during which 100J of heat is supplied to it and it does 20J of work. The system is brough back to its original state through a process during which 20 J of heat is released by the gas. What is the work done by the gas in the second process?
60 J
40 J
80 J
20 J
The correct Answer is:A
To solve the problem, we will apply the first law of thermodynamics, which states that the change in internal energy (ΔU) of a system is equal to the heat added to the system (Q) minus the work done by the system (W). This can be expressed as:
ΔQ=ΔU+ΔW
1. Identify the Given Values for the First Process:
- Heat supplied to the gas (Q1) = +100 J (since heat is supplied, it is positive)
- Work done by the gas (W1) = +20 J (work done by the system is positive)
2. Calculate the Change in Internal Energy (ΔU1) for the First Process:
Using the first law of thermodynamics:
Q1=ΔU1+W1
Substituting the known values:
100=ΔU1+20
Rearranging gives:
ΔU1=100−20=80 J
3. Identify the Given Values for the Second Process:
- Heat released by the gas (Q2) = -20 J (since heat is released, it is negative)
- Change in internal energy (ΔU2) will be the same in magnitude but opposite in sign to ΔU1, so:
ΔU2=−80 J
4. Apply the First Law of Thermodynamics for the Second Process:
Using the first law again:
Q2=ΔU2+W2
Substituting the known values:
−20=−80+W2
Rearranging gives:
W2=−20+80=60 J
5. Conclusion:
The work done by the gas in the second process is 60 J.
- Heat supplied to the gas (Q1) = +100 J (since heat is supplied, it is positive)
- Work done by the gas (W1) = +20 J (work done by the system is positive)
Using the first law of thermodynamics:
Q1=ΔU1+W1
Substituting the known values:
100=ΔU1+20
Rearranging gives:
ΔU1=100−20=80 J
- Heat released by the gas (Q2) = -20 J (since heat is released, it is negative)
- Change in internal energy (ΔU2) will be the same in magnitude but opposite in sign to ΔU1, so:
ΔU2=−80 J
Using the first law again:
Q2=ΔU2+W2
Substituting the known values:
−20=−80+W2
Rearranging gives:
W2=−20+80=60 J
The work done by the gas in the second process is 60 J.
Topper's Solved these Questions
Similar Questions
Knowledge Check
An ideal gas is taken through cycle A→B→C−A, as shown in Fig. IF the net heat supplied to the gas in the cycle is 5 J, the work done by the gas in the process C→A is
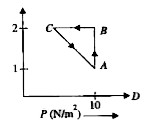 A−5JB−10JC−15JD−20J
A−5JB−10JC−15JD−20J
An ideal gas goes from the state i to the state ∫ as shown in .the work done by the gas during the process

View SolutionFind the change in internal energy if heat supplied to the gaseous system is 100 J and work done by the system is 80 J.
View SolutionA gas undergoes change from state A to state B. In this process, the heat absorbed and work done by the gas is 5 J and 8 J, respectively. Now gas is brought back to A by another process during which 3 J of heat is evolved. In this reverse process of B to A:
View SolutionA sample of ideal gas (γ=1.4) is heated at constant pressure. If an amount of 100 J heat is supplied to the gas, the work done by the gas is
View SolutionA perfect gas goes from a state A to another state B by absorbing 8 × 105 J of heat and doing 6.5 × 105 J of external work. It is now transferred between the same two states in another process in which it absorbs 105 J of heat. In the second process work done by the gas is ?
View SolutionAn ideal gas is taken through the cycle A→B→C→A, as shown in the figure, If the net heat supplied to the gas in the cycle is 5J, the work done by the gas in the process CtoA is
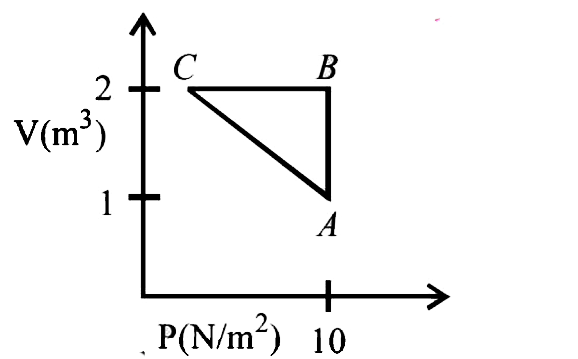
View SolutionFor a gaseous state if heat supplied to the system is 100 J and work done by the system is 25 J. then internal energy of the system is
View Solution

