A body moves along a curved path of a quarter circle. Calculate the ratio of distance to displacement :
11:7
7:11
11:√2×7
7:11√2
The correct Answer is:C
To solve the problem of finding the ratio of distance to displacement for a body moving along a curved path of a quarter circle, we can follow these steps:
1. Understand the Path:
The body moves along a quarter circle from point A to point B. This means the path taken is a quarter of the circumference of a circle.
2. Calculate the Distance:
The distance traveled along the quarter circle can be calculated using the formula for the circumference of a circle, which is C=2πR. For a quarter circle, the distance D is:
D=14×2πR=πR2
(Note: The video transcript incorrectly used 22/7 instead of π. For the sake of this solution, we will use π for accuracy.)
3. Calculate the Displacement:
The displacement is the straight line distance from point A to point B. In this case, since it forms a right triangle (with both legs equal to the radius R), we can use the Pythagorean theorem:
S=√R2+R2=√2R2=R√2
4. Calculate the Ratio of Distance to Displacement:
Now we can find the ratio of distance to displacement:
Ratio=DS=πR2R√2=π2√2
5. Simplify the Ratio:
To express the ratio in a simplified form, we can multiply the numerator and denominator by √2:
Ratio=π√24
Final Result:
The ratio of distance to displacement is:
π√24
The body moves along a quarter circle from point A to point B. This means the path taken is a quarter of the circumference of a circle.
The distance traveled along the quarter circle can be calculated using the formula for the circumference of a circle, which is C=2πR. For a quarter circle, the distance D is:
D=14×2πR=πR2
(Note: The video transcript incorrectly used 22/7 instead of π. For the sake of this solution, we will use π for accuracy.)
The displacement is the straight line distance from point A to point B. In this case, since it forms a right triangle (with both legs equal to the radius R), we can use the Pythagorean theorem:
S=√R2+R2=√2R2=R√2
Now we can find the ratio of distance to displacement:
Ratio=DS=πR2R√2=π2√2
To express the ratio in a simplified form, we can multiply the numerator and denominator by √2:
Ratio=π√24
The ratio of distance to displacement is:
π√24
Topper's Solved these Questions
- Motion in Straight Line BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - IN-CHAPTER EXERCISE-B
10 Videos
- Motion in Straight Line BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - IN-CHAPTER EXERCISE-C
10 Videos
- Motion in Straight Line BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - PRACTICE EXERCISE
80 Videos
- MOTION IN A STRAIGHT LINE & PLANE BOOK - VMC MODULES ENGLISHCHAPTER - MOTION IN A STRAIGHT LINE & PLANE EXERCISE - IMPECCABLE
52 Videos
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - MCQ
2 Videos
Similar Questions
A body covered a distance of Lm along a curved path of a quarter circle. The ratio of distance to displacements.
View SolutionA body covers a circular path of radius R in 20 second. Calculate the distance and the displacement of of body at the end of 50 second.
View SolutionCan a body move on a curved path without having acceleration ?
View SolutionAn object covers 1/4 of the circular path, what will be the ratio of the distance and displacement of the object ?
View SolutionA particle moves along a path ABCD as shown in the figure. Then the magnitude of net displacement of the particle from position A to D is:

View SolutionA particle moves over three quarters of a circle of radius r. What is the magnitude of its displacement ?
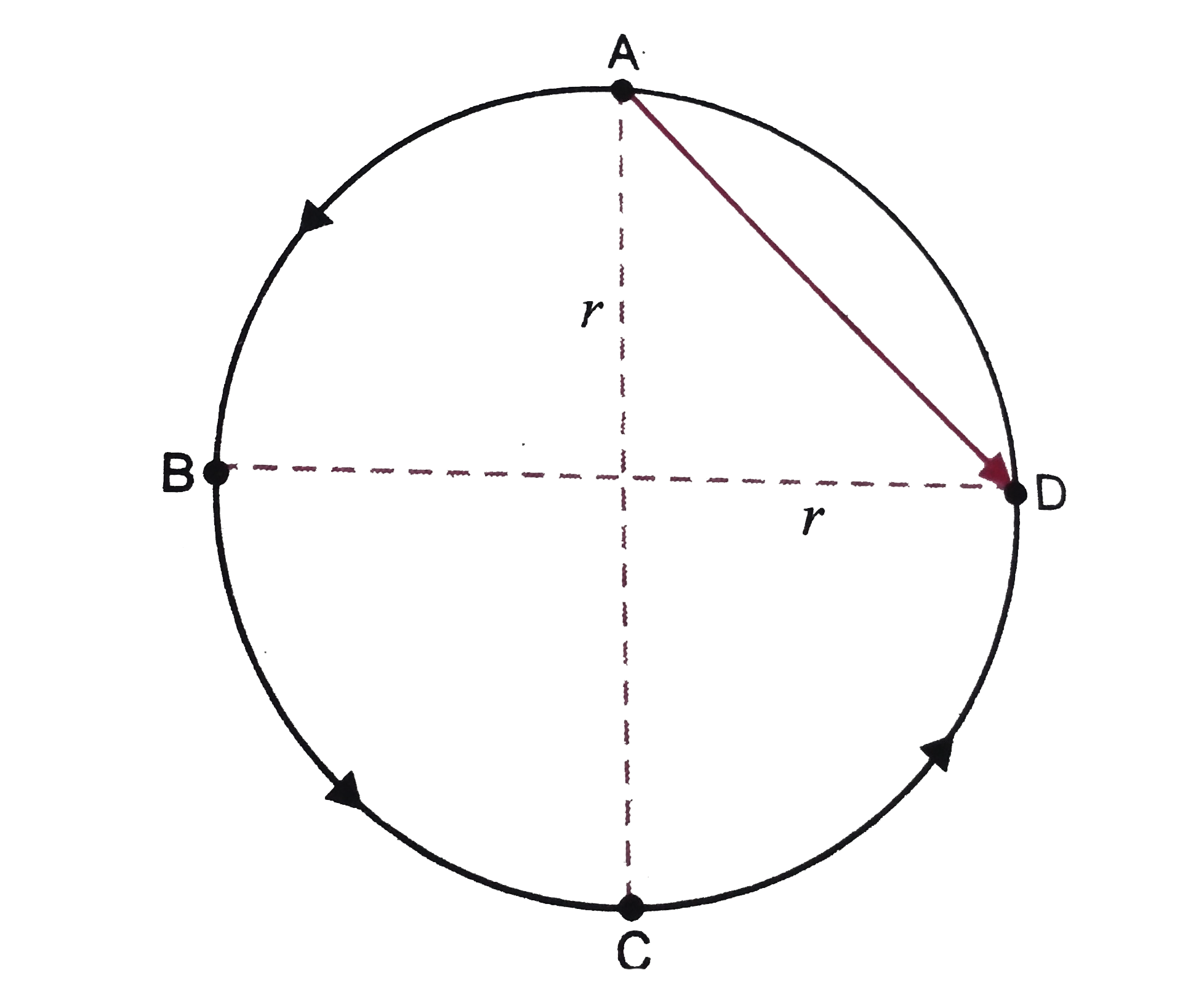
View SolutionA particle moves along a circular path of radius R. The distance and displacement of a particle after one completer revolution is
View SolutionA person walks along a semicircular path from A to B as shown in the figure given below.
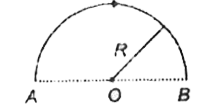
Calculate the distance and displacement traversed by the person.
View SolutionA particle moves on a circular path of radius 'r'. It completes one revolution in 40s. Calculate distances displacement in 2 min 20 s.
View SolutionA body moves along a circular path of radius 5m. The coefficient of friction between the surface of the path and the body is 0.5. The angular velocity in rad/s with which the body should move so that it does not leave the path is (g−10m/s−2)
View Solution
