Let af and at represent radial and tangential accelerations. The motion of a particle may be circlar, if
ar=0andat=0
ar=0 but ats=0
ars0 but at=0
ars0 but ats0
The correct Answer is:C
Step by step video & image solution for Let a_(f) and a_(t) represent radial and tangential accelerations. The motion of a particle may be circlar, if by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- Motion in Straight Line BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - IN-CHAPTER EXERCISE-I
10 Videos
- MOTION IN A STRAIGHT LINE & PLANE BOOK - VMC MODULES ENGLISHCHAPTER - MOTION IN A STRAIGHT LINE & PLANE EXERCISE - IMPECCABLE
52 Videos
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - MCQ
2 Videos
Similar Questions
If ar and at represent radial and tangential accelerations, the motion of a particle will be uniformly circular if
View SolutionA particle moves along a circle if radius (20 //pi) m with constant tangential acceleration. If the velocity of the particle is 80m/s at the end of the second revolution after motion has begun the tangential acceleration is .
View SolutionA particle moves along a circle if radius (20/π)m with constant tangential acceleration. If the velocity of the particle is 80m/s at the end of the second revolution after motion has begun the tangential acceleration is .
View SolutionA particle moves along a circle if radius (20 //pi) m with constant tangential acceleration. If the velocity of the particle is 80m/s at the end of the second revolution after motion has begun the tangential acceleration is .
View SolutionA particle moves in a circle with constant tangential acceleration starting from rest. At t = 1/2 s radial acceleration has a value 25% of tangential acceleration. The value of tangential acceleration will be correctly represented by
View SolutionA particle is moving along a circular path ofradius R in such a way that at any instant magnitude of radial acceleration & tangential acceleration are equal. 1f at t = 0 velocity of particle is V0. Find the speed of the particle after time t=(R)/(2V0)
View SolutionA particle is moving on a circle of radius R such that at every instant the tangential and radial accelerations are equal in magnitude. If the velocity of the particle be v0 at t=0, the time for the completion of the half of the first revolution will be
View SolutionGraphs are very useful to represent a physical situation. Various quantities can be easily represented on graphs and other quantites can be determined from the graph. For example the slope of velocity-time graph represents instantaneous acceleration. For a motion with constant acceleration slope of velocity-time graph is constant. If acceleration is changing with time, slope will change and thus velocity-time graph will be a non-linear curve. Further the area of velocity-time graph gives displacement.
The correct relation between v0,a1,a2andt0 is
View SolutionFind the relation between acceleration a1 and a2
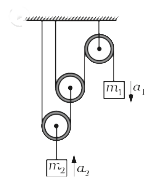
View SolutionIn a circular motion of a particle the tangential acceleration of the particle is given by a1=2m/s2. The radius of the circle described is 4 m. The particle is initially at rest. Time after which total acceleration of the particle makes 45∘ with radial acceleration is :
View Solution