A disc of radius R is placed on a square plate of edge 4R made up of the same sheet with their planes parallel such that any two adjacent sides ofsquare touch the disc. Find the distance of the centre of mass of the system from the centre of square plate?
To find the distance of the center of mass of the system (a disc placed on a square plate) from the center of the square plate, we can follow these steps:
Step 1: Understand the Geometry
- The square plate has an edge length of 4R.
- The disc has a radius of R.
- The disc is positioned such that its edges touch two adjacent sides of the square.
Step 2: Determine the Coordinates of the Centers
- The center of the square plate is at the origin (0,0).
- The center of the disc, given its position, can be determined as follows:
- The distance from the center of the square to the edge of the square is 2R (half of the side length).
- The center of the disc will be at (2R,R) since it is R above the bottom edge of the square and 2R away from the center horizontally.
Step 3: Calculate the Masses
- Let the mass of the disc be m1 and the mass of the square plate be m2.
- The area of the square plate A2=(4R)2=16R2.
- The area of the disc A1=πR2.
- Assuming uniform density, the masses can be expressed as:
m1=σA1=σπR2
m2=σA2=σ(16R2)
where σ is the mass per unit area.
Step 4: Find the Center of Mass Coordinates
- The center of mass x coordinate of the system is given by:
xcm=m1x1+m2x2m1+m2
where:
- x1=2R (x-coordinate of the disc)
- x2=0 (x-coordinate of the square plate)
Substituting the values, we have:
xcm=m1⋅2R+m2⋅0m1+m2=m1⋅2Rm1+m2
Step 5: Substitute the Masses
Substituting m1 and m2:
xcm=(σπR2)⋅2RσπR2+σ(16R2)
This simplifies to:
xcm=2RπR2πR2+16R2=2Rππ+16
Step 6: Final Distance from the Center of the Square Plate
The distance of the center of mass from the center of the square plate is:
d=xcm=2Rππ+16
Conclusion
Thus, the distance of the center of mass of the system from the center of the square plate is:
2Rππ+16
- The square plate has an edge length of 4R.
- The disc has a radius of R.
- The disc is positioned such that its edges touch two adjacent sides of the square.
- The center of the square plate is at the origin (0,0).
- The center of the disc, given its position, can be determined as follows:
- The distance from the center of the square to the edge of the square is 2R (half of the side length).
- The center of the disc will be at (2R,R) since it is R above the bottom edge of the square and 2R away from the center horizontally.
- Let the mass of the disc be m1 and the mass of the square plate be m2.
- The area of the square plate A2=(4R)2=16R2.
- The area of the disc A1=πR2.
- Assuming uniform density, the masses can be expressed as:
m1=σA1=σπR2
m2=σA2=σ(16R2)
where σ is the mass per unit area.
- The center of mass x coordinate of the system is given by:
xcm=m1x1+m2x2m1+m2
where:
- x1=2R (x-coordinate of the disc)
- x2=0 (x-coordinate of the square plate)
Substituting the values, we have:
xcm=m1⋅2R+m2⋅0m1+m2=m1⋅2Rm1+m2
Substituting m1 and m2:
xcm=(σπR2)⋅2RσπR2+σ(16R2)
This simplifies to:
xcm=2RπR2πR2+16R2=2Rππ+16
The distance of the center of mass from the center of the square plate is:
d=xcm=2Rππ+16
Thus, the distance of the center of mass of the system from the center of the square plate is:
2Rππ+16
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - SOLVED EXAMPLES20videos
SYSTEM OF A PARTICLES & ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE-14videos
SYSTEM OF A PARTICLES & ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question46videos
SIMPLE HARMONIC MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - IMPECCABLE56videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
Similar Questions
Centre of mass of the system lies inside disc or square plate and why ?
View SolutionFour point masses are placed at the corners of a square of side 2 m as shown in the figure. Find the centre of mass of the system w.r.t. the centre of square.
 View Solution
View SolutionFrom a circular disc of radius R, a triangular portion is cut (sec figure). The distance of the centre of mass of the remainder from the centre of the disc is −
 View Solution
View SolutionA solid sphere of radius R is placed on a cube of side 2R. Both are made of same material. Find the distance of their centre of mass fro the interface.
View SolutionA square lamina of side a and a circular lamina of diameter a are placed touching each other as shown in figure. Find distance of their centre of mass from point O, the centre of square.
 View Solution
View SolutionThere is a thin uniform disc of radius R and mass per unit area σ in which a hole of radius R/2 has been cut out as shown in the figure. Inside the hole, a square plate of same mass per unit area σ is inserted so that its corners touch the periphery of the hole. The distance of the centre of mass of the system from the origin is
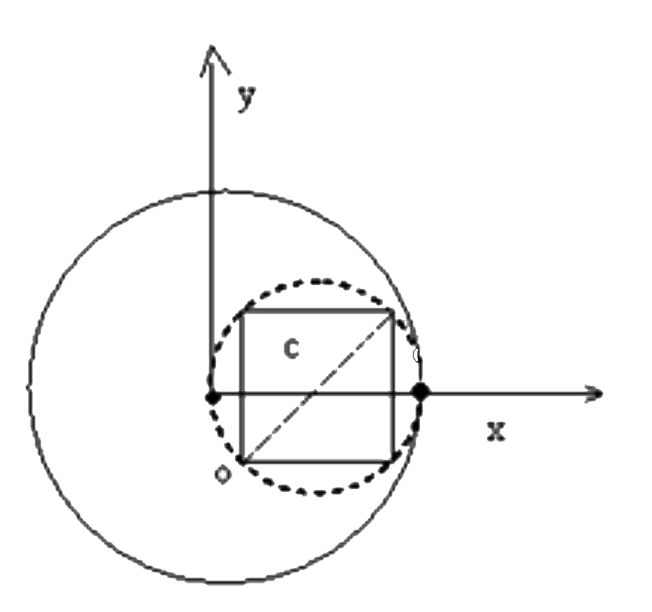 View Solution
View SolutionA uniform square plate and a disc having same mass per unit area are kept in contact as shown in Fig. The side of square and diameter of circle are both equal to L. Locate the position of centre of mass of the system w.r.t. the centre of the square.
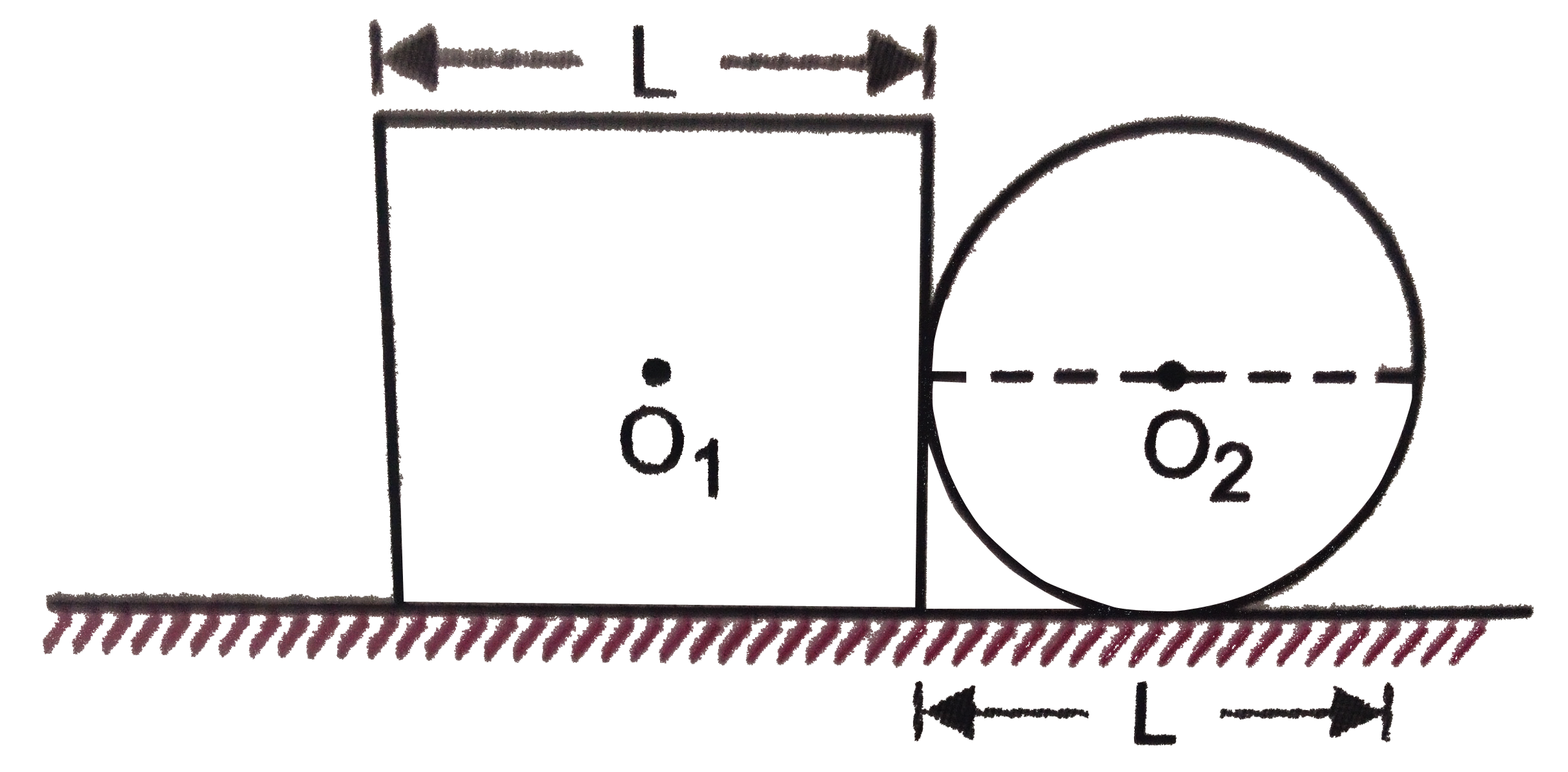 View Solution
View SolutionA disc of radis R is cut out from a larger disc of radius 2R in such a way that the edge of the hole touches the edge of the disc. Locate the centre of mass of the residual disc.
View SolutionA uniform disc of radius R is put over another unifrom disc of radius 2R of the same thickness and density. The peripheries of the two discs touch each other. Locate the centre of mass of the system.
View SolutionA disc of radius r is cut from a larger disc of radius 4r in such a way that the edge of the hole touches the edge of the disc. The centre of mass of the residual disc will be a distance from centre of larger disc :-
View Solution

