4 Masses 8 kg, 2 kg, 4 kg and 2 kg are placed at the corners A, B, C, D respectively of a square ABCD of diagonal 80 cm. The distance of centre of mass from A will be
To find the distance of the center of mass from point A in the given problem, we will follow these steps:
Step 1: Determine the side length of the square
Given that the diagonal of the square ABCD is 80 cm, we can find the side length (a) using the relationship:
Diagonal=a√2
So,
80=a√2⟹a=80√2=40√2 cm
Step 2: Assign coordinates to the masses
We will assign coordinates to the corners of the square based on the standard Cartesian coordinate system:
- Mass mA=8kg at point A (0, 0)
- Mass mB=2kg at point B (40√2,0)
- Mass mC=4kg at point C (40√2,40√2)
- Mass mD=2kg at point D (0,40√2)
Step 3: Calculate the total mass
The total mass M is given by:
M=mA+mB+mC+mD=8+2+4+2=16kg
Step 4: Calculate the coordinates of the center of mass
The coordinates of the center of mass (x_cm, y_cm) can be calculated using the formula:
xcm=mAxA+mBxB+mCxC+mDxDM
ycm=mAyA+mByB+mCyC+mDyDM
Substituting the values:
xcm=8⋅0+2⋅(40√2)+4⋅(40√2)+2⋅016
=0+80√2+160√2+016=240√216=15√2
ycm=8⋅0+2⋅0+4⋅(40√2)+2⋅(40√2)16
=0+0+160√2+80√216=240√216=15√2
Thus, the coordinates of the center of mass are:
(xcm,ycm)=(15√2,15√2)
Step 5: Calculate the distance from point A
The distance d from point A (0, 0) to the center of mass can be calculated using the distance formula:
d=√(xcm−xA)2+(ycm−yA)2
Substituting the values:
d=√(15√2−0)2+(15√2−0)2
=√(15√2)2+(15√2)2=√2⋅(15√2)2=√2⋅450=√900=30cm
Final Answer
The distance of the center of mass from point A is 30 cm.
---
Given that the diagonal of the square ABCD is 80 cm, we can find the side length (a) using the relationship:
Diagonal=a√2
So,
80=a√2⟹a=80√2=40√2 cm
We will assign coordinates to the corners of the square based on the standard Cartesian coordinate system:
- Mass mA=8kg at point A (0, 0)
- Mass mB=2kg at point B (40√2,0)
- Mass mC=4kg at point C (40√2,40√2)
- Mass mD=2kg at point D (0,40√2)
The total mass M is given by:
M=mA+mB+mC+mD=8+2+4+2=16kg
The coordinates of the center of mass (x_cm, y_cm) can be calculated using the formula:
xcm=mAxA+mBxB+mCxC+mDxDM
ycm=mAyA+mByB+mCyC+mDyDM
xcm=8⋅0+2⋅(40√2)+4⋅(40√2)+2⋅016
=0+80√2+160√2+016=240√216=15√2
=0+0+160√2+80√216=240√216=15√2
(xcm,ycm)=(15√2,15√2)
The distance d from point A (0, 0) to the center of mass can be calculated using the distance formula:
d=√(xcm−xA)2+(ycm−yA)2
Substituting the values:
d=√(15√2−0)2+(15√2−0)2
=√(15√2)2+(15√2)2=√2⋅(15√2)2=√2⋅450=√900=30cm
The distance of the center of mass from point A is 30 cm.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE-25videos
SYSTEM OF A PARTICLES & ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE-35videos
SYSTEM OF A PARTICLES & ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - SOLVED EXAMPLES20videos
SYSTEM OF A PARTICLES & ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question46videos
SIMPLE HARMONIC MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - IMPECCABLE56videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
Similar Questions
Three particles of masses 1kg, 2kg and 3kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1m. Find the distance of their centre of mass from A.
View SolutionFour particles of masses 1kg,2kg,3kg and 4kg are placed the four vertices A,B,C and D, respectively, of a square of side 1m. Find the position of centre of mass of the particles.
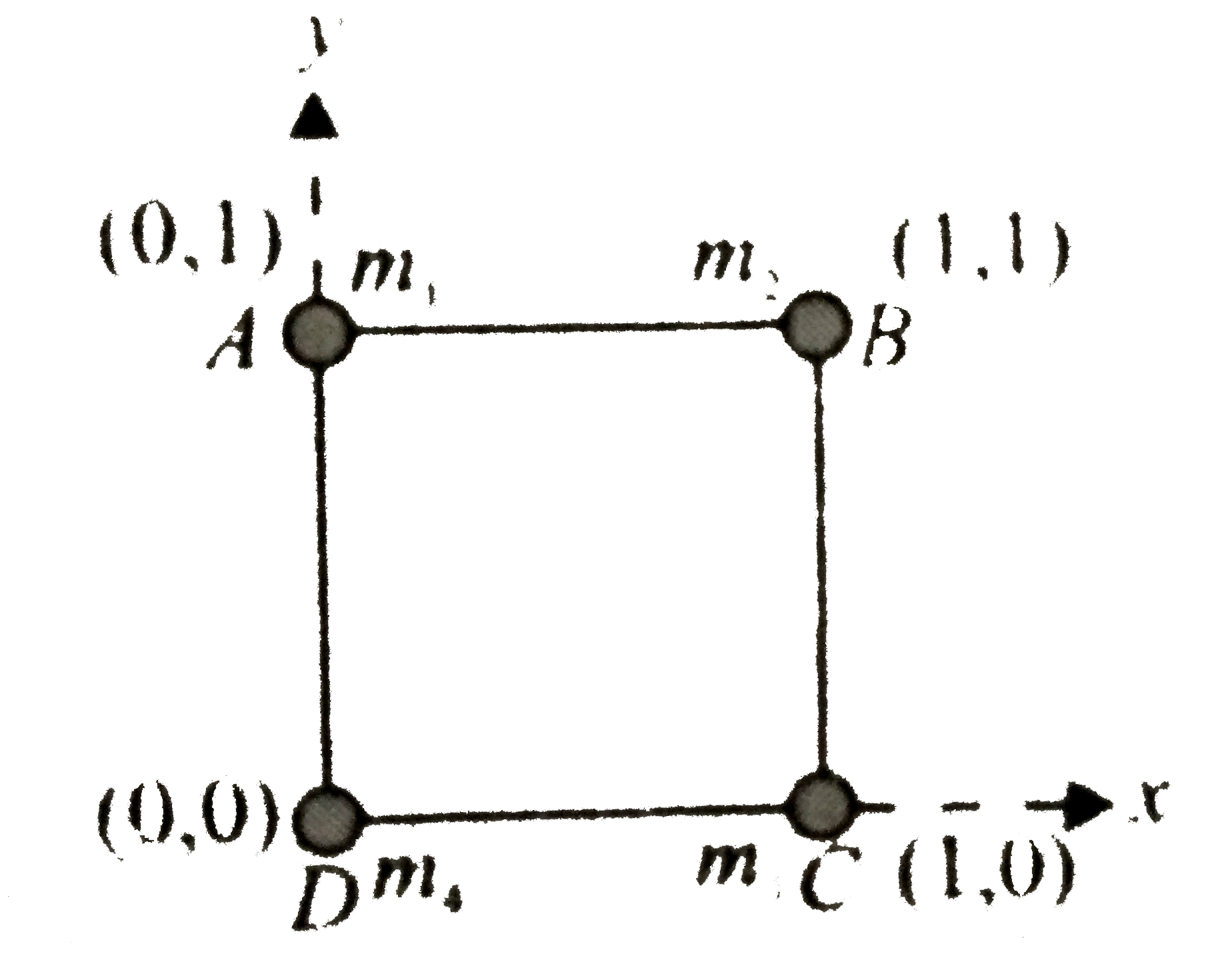 View Solution
View SolutionFour particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A,B,C and D of a square of side 1m. Find square of distance of their centre of mass from A.
View SolutionThree particles of masses 1.0 kg 2.0 kg and 3.0 kg are placed at the corners A,B and C respectively of an equilateral triangle ABC of edge 1m. Locate the centre of mass of the system.
View SolutionFour particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A, B, C and D of a square of side 1m. Find the position of centre of mass of the particles.
View SolutionFour particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A, B, C and D of a square of side 1m. Find the position of centre of mass of the particles. Assume that D is situated at the origin.
View SolutionFour particles of masses 2,2,4,4 kg are arranged at the corners A,B,C,D of a square ABCD of side 2m as shown in the figure. The perpendicular distance of their centre of mass from the side AB is
 View Solution
View SolutionFour point masses 1 kg, 1 kg, 2 kg and 2 kg are placed at the corners of a square of side a m as shown in Fig. Find the centre of mass of the system.
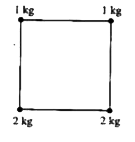 View Solution
View SolutionFour point particles of masses 1.0 kg, 1.5 kg, 3.0 kg and 2.5 kg are placed at four corners of a rectangle of sides 4.0 cm and 3.0 cm as shown in the figure. The centre of mass of the system is at a point:
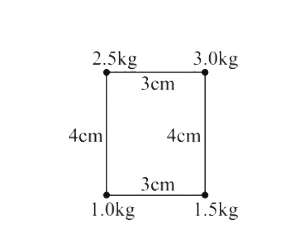 View Solution
View SolutionFour point particles of masses 1.0 kg, 1.5 kg, 3.0 kg and 2.5 kg are placed at four corners of a rectangle of sides 4.0 cm and 3.0 cm as shown in the figure. The centre of mass of the system is at a point:
 View Solution
View Solution

