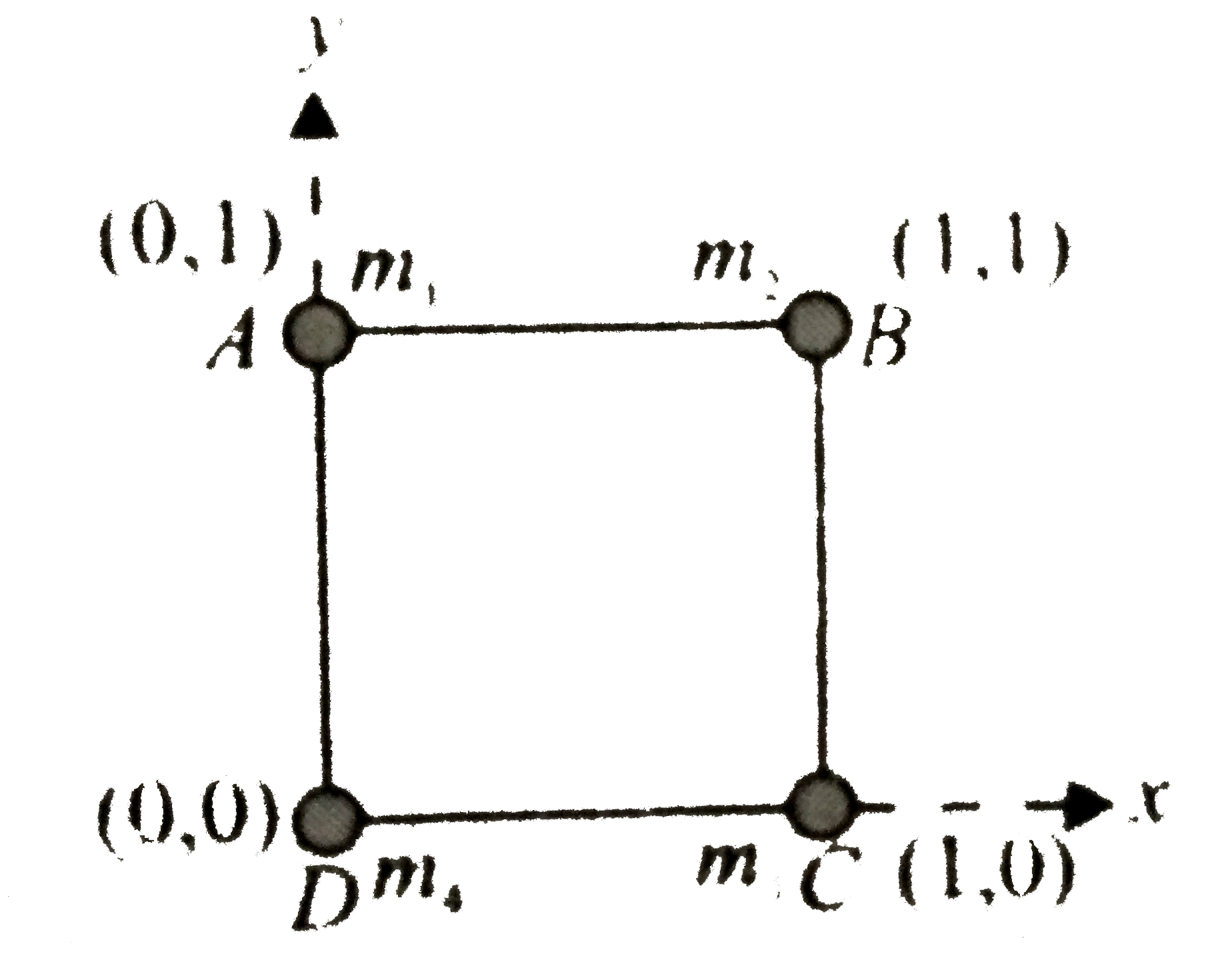
Four particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A, B, C and D of a square of side 1m. Find the position of centre of mass of the particles.
The correct Answer is:C
To find the position of the center of mass of the four particles placed at the vertices of a square, we can follow these steps:
Step 1: Define the coordinates of the vertices
Let’s assign the coordinates of the vertices of the square:
- Vertex A (0, 0) for mass mA=1kg
- Vertex B (1, 0) for mass mB=2kg
- Vertex C (1, 1) for mass mC=3kg
- Vertex D (0, 1) for mass mD=4kg
Step 2: Calculate the total mass
The total mass M of the system is the sum of the individual masses:
M=mA+mB+mC+mD=1+2+3+4=10kg
Step 3: Calculate the x-coordinate of the center of mass
The x-coordinate of the center of mass xcm is given by the formula:
xcm=mAxA+mBxB+mCxC+mDxDM
Substituting the values:
xcm=(1×0)+(2×1)+(3×1)+(4×0)10
Calculating the numerator:
=0+2+3+010=510=0.5m
Step 4: Calculate the y-coordinate of the center of mass
The y-coordinate of the center of mass ycm is given by:
ycm=mAyA+mByB+mCyC+mDyDM
Substituting the values:
ycm=(1×0)+(2×0)+(3×1)+(4×1)10
Calculating the numerator:
=0+0+3+410=710=0.7m
Step 5: Conclusion
The position of the center of mass of the four particles is:
Center of Mass=(xcm,ycm)=(0.5m,0.7m)
---
Let’s assign the coordinates of the vertices of the square:
- Vertex A (0, 0) for mass mA=1kg
- Vertex B (1, 0) for mass mB=2kg
- Vertex C (1, 1) for mass mC=3kg
- Vertex D (0, 1) for mass mD=4kg
The total mass M of the system is the sum of the individual masses:
M=mA+mB+mC+mD=1+2+3+4=10kg
The x-coordinate of the center of mass xcm is given by the formula:
xcm=mAxA+mBxB+mCxC+mDxDM
Substituting the values:
xcm=(1×0)+(2×1)+(3×1)+(4×0)10
Calculating the numerator:
=0+2+3+010=510=0.5m
The y-coordinate of the center of mass ycm is given by:
ycm=mAyA+mByB+mCyC+mDyDM
Substituting the values:
ycm=(1×0)+(2×0)+(3×1)+(4×1)10
Calculating the numerator:
=0+0+3+410=710=0.7m
The position of the center of mass of the four particles is:
Center of Mass=(xcm,ycm)=(0.5m,0.7m)
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Type 1
1 Video
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Solved Examples
13 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
Four particles of masses 1kg,2kg,3kg and 4kg are placed the four vertices A,B,C and D, respectively, of a square of side 1m. Find the position of centre of mass of the particles.
View SolutionFour particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A,B,C and D of a square of side 1m. Find square of distance of their centre of mass from A.
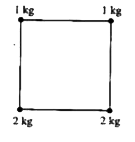
View SolutionFour point masses 1 kg, 1 kg, 2 kg and 2 kg are placed at the corners of a square of side a m as shown in Fig. Find the centre of mass of the system.
View Solution4 Masses 8 kg, 2 kg, 4 kg and 2 kg are placed at the corners A, B, C, D respectively of a square ABCD of diagonal 80 cm. The distance of centre of mass from A will be
View SolutionThree particles of masses 1kg, 2kg and 3kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1m. Find the distance of their centre of mass from A.
View SolutionThree particles of masses 1.0 kg 2.0 kg and 3.0 kg are placed at the corners A,B and C respectively of an equilateral triangle ABC of edge 1m. Locate the centre of mass of the system.
View SolutionFour particles having masses, m, 2m, 3m, and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the centre.
View SolutionFour particles having masses, m, 2m, 3m, and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the centre.
View SolutionFour particles having masses, m, 2m, 3m, and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the center.
View SolutionFind the potential energy of 4-particles, each of mass 1 kg placed at the four vertices of a square of side length 1 m.
View Solution