Three equal resistances connected is series across a source of e.m.f consume 20 watt. If the same resistor are connected in parallel across the same source of e.m.f., what would be the power dissipated ?
The correct Answer is:180W
To solve the problem, we will follow these steps:
Step 1: Understand the initial conditions
We have three equal resistances (let's denote each resistance as R) connected in series across a source of EMF (E). The power consumed in this configuration is given as 20 watts.
Step 2: Calculate the equivalent resistance in series
When resistances are connected in series, the total resistance Rs is the sum of the individual resistances:
Rs=R+R+R=3R
Step 3: Use the power formula for the series connection
The power consumed in a circuit can be calculated using the formula:
P=E2R
For the series connection, we can substitute R with Rs:
20=E23R
From this, we can express E2:
E2=20×3R=60R(Equation 1)
Step 4: Calculate the equivalent resistance in parallel
Now, we will consider the case when the same resistors are connected in parallel. The equivalent resistance Rp for three equal resistances in parallel is given by:
1Rp=1R+1R+1R=3R
Thus, we can find Rp:
Rp=R3
Step 5: Use the power formula for the parallel connection
Now we will calculate the power consumed when the resistors are connected in parallel:
P′=E2Rp
Substituting Rp:
P′=E2R3=3⋅E2R(Equation 2)
Step 6: Substitute E2 from Equation 1 into Equation 2
Now we will substitute E2 from Equation 1 into Equation 2:
P′=3⋅60RR=3⋅60=180 watts
Final Answer
The power dissipated when the resistors are connected in parallel is 180 watts.
---
We have three equal resistances (let's denote each resistance as R) connected in series across a source of EMF (E). The power consumed in this configuration is given as 20 watts.
When resistances are connected in series, the total resistance Rs is the sum of the individual resistances:
Rs=R+R+R=3R
The power consumed in a circuit can be calculated using the formula:
P=E2R
For the series connection, we can substitute R with Rs:
20=E23R
From this, we can express E2:
E2=20×3R=60R(Equation 1)
Now, we will consider the case when the same resistors are connected in parallel. The equivalent resistance Rp for three equal resistances in parallel is given by:
1Rp=1R+1R+1R=3R
Thus, we can find Rp:
Rp=R3
Now we will calculate the power consumed when the resistors are connected in parallel:
P′=E2Rp
Substituting Rp:
P′=E2R3=3⋅E2R(Equation 2)
Now we will substitute E2 from Equation 1 into Equation 2:
P′=3⋅60RR=3⋅60=180 watts
The power dissipated when the resistors are connected in parallel is 180 watts.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-A
10 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-B
10 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE EXERCISE
11 Videos
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Advance ( Archive ) LEVEL 48
1 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - JEE ADVANCED ARCHIVE
68 Videos
Similar Questions
Three equal resistor connected in series across a source of enf together dissipate 10Wa. If the same resistors aer connected in parallel across the same emf, then the power dissipated will be
View SolutionThree equal resistors connected in series across a source of emf together dissipate 10W of power. What would be the power dissipated if te same resistors are connected in parallel across the same source of emf?
View SolutionThree equal resistors connected in series across a source of e.m.f. together dissipate 10 W of power. What should be the power dissipated if the same resistors are connected in parallel across the same source of e.m.f.
View SolutionThe equivalent resistance across the terminals of source of e.m.f. 24V for the circuit shown in the figure is
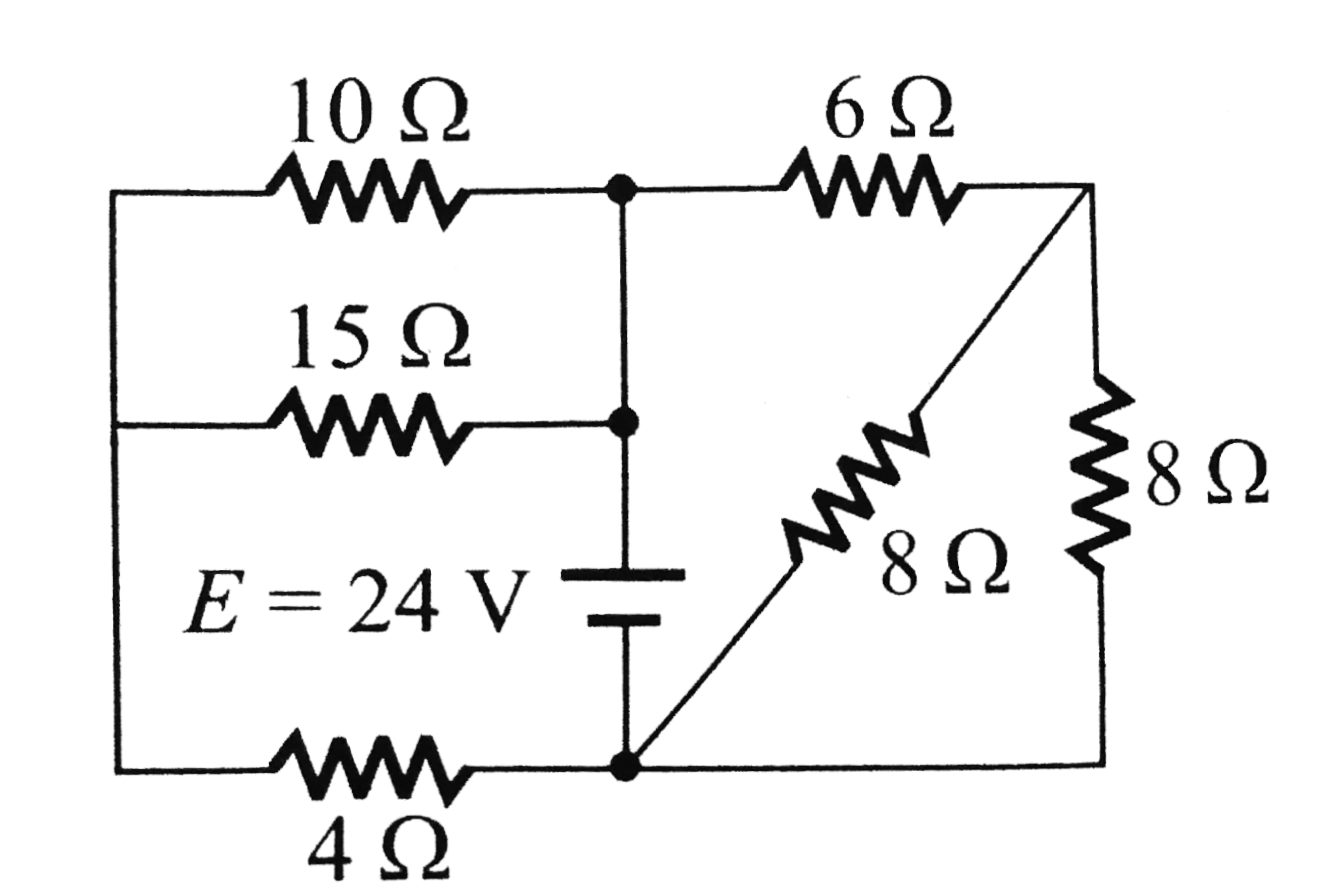
View SolutionTwo bulbs when connected in parallel to a source take 60 W each, the power consumed, when they are connected in series with the same source is
View SolutionThe ratio of distance of two satellites from the centre of earth is 1 : 4. The ratio of their time periods of rotation will be :
View SolutionTwo bulbs when connected in parallel to a source take 100 W each. The total power consumed when they are connected in series with the same source is
View SolutionPower generated across a uniform wire connected across a supply is H. If the wire is cut into n equal parts and all the parts are connected in parallel across the same supply, the total power generated in the wire is
View SolutionTwo bulbs 60 W and 100 W designed for voltage 220 V are connected in series across 220 V source. The net power dissipated is
View SolutionFour equal resistance dissipated 5 W of power together when connected in series to a battery of negligible internal resistance . The total power dissipated in these resistance when connected in parallel across the same battery would be .
View Solution
