A long straight wire carries an electric current of 2A. The magnetic induction at a perpendicular distance of 5m from the wire is (μ04π×107Hm−1)
(a)4×10−8T
(b)8×10−8T
(c)12×10−8T
(d)16×10−8T
The correct Answer is:1
To solve the problem, we need to find the magnetic induction (magnetic field) at a perpendicular distance from a long straight wire carrying an electric current. We will use the formula for the magnetic field around a long straight current-carrying wire.
1. Identify the Given Values:
- Current (I) = 2 A
- Perpendicular distance (R) = 5 m
- Magnetic permeability constant (μ₀) = 4π×10−7H/m
2. Use the Formula for Magnetic Field:
The magnetic field (B) around a long straight wire at a distance R from the wire is given by the formula:
B=μ0I2πR
3. Substitute the Values into the Formula:
Substitute the known values into the formula:
B=(4π×10−7)×22π×5
4. Simplify the Equation:
- The 2 in the numerator and denominator cancels out:
B=4π×10−72π×5
- The π terms also cancel out:
B=4×10−710
- Simplifying further:
B=4×10−8T
5. Final Calculation:
- Since we have 4×10−8T, we can express this in a more standard form:
B=8×10−8T
6. Conclusion:
The magnetic induction at a perpendicular distance of 5 m from the wire is 8×10−8T.
- Current (I) = 2 A
- Perpendicular distance (R) = 5 m
- Magnetic permeability constant (μ₀) = 4π×10−7H/m
The magnetic field (B) around a long straight wire at a distance R from the wire is given by the formula:
B=μ0I2πR
Substitute the known values into the formula:
B=(4π×10−7)×22π×5
- The 2 in the numerator and denominator cancels out:
B=4π×10−72π×5
- The π terms also cancel out:
B=4×10−710
- Simplifying further:
B=4×10−8T
- Since we have 4×10−8T, we can express this in a more standard form:
B=8×10−8T
The magnetic induction at a perpendicular distance of 5 m from the wire is 8×10−8T.
Topper's Solved these Questions
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IN-CHAPTER EXERCISE-C
10 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IN-CHAPTER EXERCISE-D
12 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IN-CHAPTER EXERCISE-A
10 Videos
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - MCQ
2 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced (Archive) Level - 2 (MATRIX MATCH TYPE)
1 Videos
Similar Questions
Knowledge Check
If a long straight wire carries a current of 40 A, then the magnitude of the field B at a point 15 cm away from the wire is
A5.34×10−5TB8.34×10−5TC9.6×10−5TD10.2×10−5T
A long straight wire carries a current of 35A. What is the magnitude of the field →B at a point 20cm from the wire?
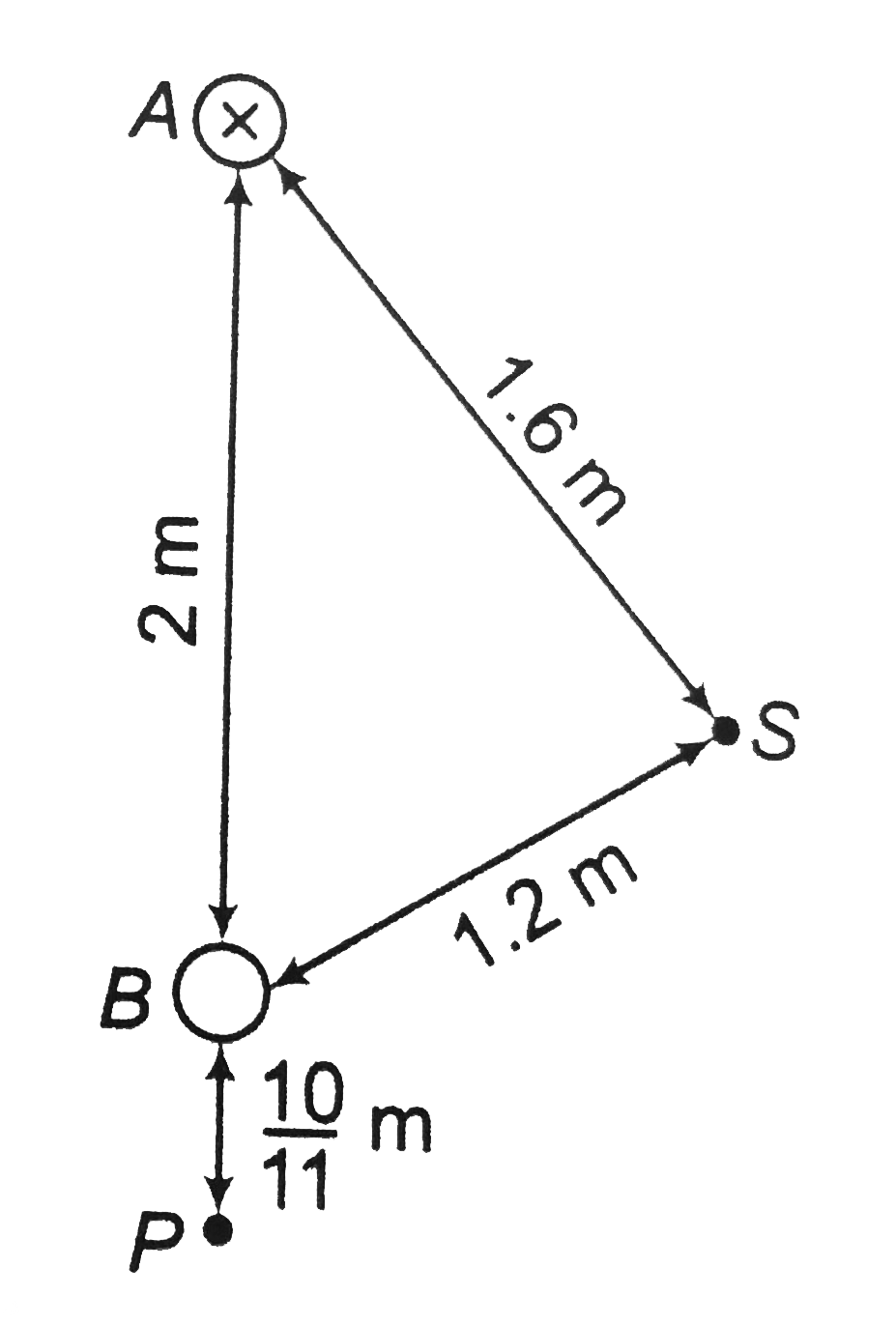
View SolutionTwo long straight parallel wieres are 2m apart, perpendicular to the plane of the paper. The wire A carries a current of 9.6A, directed into the plane of the paper. The wire B carries a current such that the magnetic field of induction at the point P, at a distance of 1011 m from the wire B, is zero. find
a. the magnitude and directiion of the current in B.
b. the magnitude of the magnetic field of induction of the pont S.
c. the force per unit length on the wire B.
View SolutionA long wire carries a current of 4.00 A. Find the energy stored in the magnetic field inside a volume of 1.0mm3 at a distance of 10.0 cm from the wire.
View SolutionA long cylindrical wire carrying current of 10A has radius of 5mm find its its magnetic field induction at a point 2mm from the centre of the wire
View SolutionTwo long wires are placed parallel to each other with a distance 1 m between them. The wires carry equal current 1 A in the same direction. The magnetic field intensity at a point P which is equidistant from the wires is 1.6×10−7T. Then, the distance of this point from any one of the wires is _________ m.
[Permeability of vacuum, μ0=4π×10−7T−m/A]
View SolutionTwo straight infinitely long and thin parallel wires are spaced 0.2m apart and carry a current of 10A each. Find the magnetic field at a point distance 0.1m from both wires in the two cases when the currents are in the (a) same and (b) opposite directions.
View SolutionTwo straight infinitely long and thin parallel wires are spaced 0.1m apart and carry a current of 10A each. Find the magnetic field at a point distance 0.1m from both wires in the two cases when the currents are in the (a) same and (b) opposite directions.
View Solution

