The magnetic field in a certain region is given by B=(4.0→i−1.8→k)×10−3T. How much flux passes through a 5.0cm2 area loop in this region if the loop lies flat on the xy-plane?
−0.9μWb
−1.0μWb
-0.03μWb
−0.04μWb
The correct Answer is:A
To find the magnetic flux passing through a loop in a magnetic field, we can use the formula for magnetic flux, which is given by:
Φ=B⋅A
where:
- Φ is the magnetic flux,
- B is the magnetic field vector,
- A is the area vector of the loop.
Step 1: Identify the magnetic field vector
The magnetic field is given as:
B=(4.0^i−1.8^k)×10−3T
Step 2: Determine the area vector
The area of the loop is given as 5.0cm2. We need to convert this to square meters:
Area=5.0cm2=5.0×10−4m2
Since the loop lies flat on the xy-plane, the direction of the area vector A will be along the z-axis:
A=5.0×10−4^km2
Step 3: Calculate the dot product
Now we can calculate the magnetic flux using the dot product:
Φ=B⋅A=(4.0^i−1.8^k)×10−3⋅(5.0×10−4^k)
Calculating the dot product:
Φ=(4.0×10−3^i⋅5.0×10−4^k)+(−1.8×10−3^k⋅5.0×10−4^k)
Since ^i⋅^k=0 and ^k⋅^k=1:
Φ=0−(1.8×5.0)×10−3×10−4
Φ=−9.0×10−7Wb
Step 4: Convert to microWebers
To express the flux in microWebers:
Φ=−9.0×10−7Wb=−0.9μWb
Conclusion
The magnetic flux passing through the loop is:
Φ=−0.9μWb
- Φ is the magnetic flux,
- B is the magnetic field vector,
- A is the area vector of the loop.
The magnetic field is given as:
B=(4.0^i−1.8^k)×10−3T
The area of the loop is given as 5.0cm2. We need to convert this to square meters:
Area=5.0cm2=5.0×10−4m2
A=5.0×10−4^km2
Now we can calculate the magnetic flux using the dot product:
Φ=B⋅A=(4.0^i−1.8^k)×10−3⋅(5.0×10−4^k)
Φ=(4.0×10−3^i⋅5.0×10−4^k)+(−1.8×10−3^k⋅5.0×10−4^k)
Since ^i⋅^k=0 and ^k⋅^k=1:
Φ=0−(1.8×5.0)×10−3×10−4
Φ=−9.0×10−7Wb
To express the flux in microWebers:
Φ=−9.0×10−7Wb=−0.9μWb
The magnetic flux passing through the loop is:
Φ=−0.9μWb
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - IN-CHAPTER EXERCISE-B
10 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - IN-CHAPTER EXERCISE-C
10 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - PRACTICE EXERCISE 5
5 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
31 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE
52 Videos
Similar Questions
The magnetic field in a certain region is given by B=(4.0→i−1.8→k)×10−3T. How much flu passes through a 5.0cm2 area loop in this region if the loop lies flat on the xy-plane?
View SolutionThe electric field in a region is given by →E=35E0→i+45E0→j with E0=2.0×103NC−1. Find the flux of this field through a recatngular surface of area 0.2m2 parallel to the y-z plane.
View SolutionThe electric field in a region is given by E=35E0ˆi+45E0j with E0=2.0×103N/C. Find the flux of this field through a rectangular surface of area 0.2m2 parallel to the y-z plane.
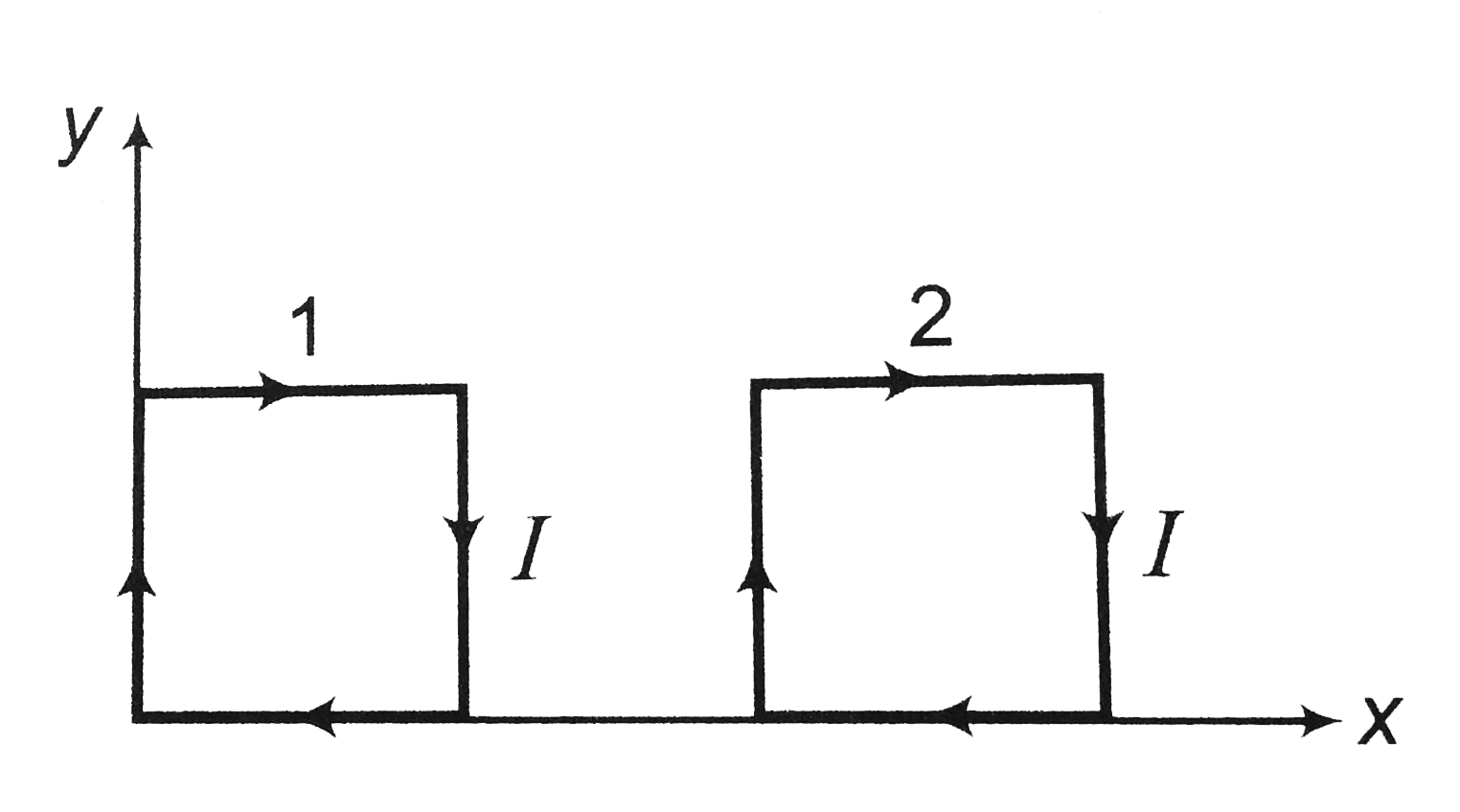
View SolutionMagnetic field in a region is given by B=B0xˆk. Two loops each of side a is placed in the magnetic region in the xy-plane with one of its sides on x-axis. If F1 is the force on loop 1 and dF2 be the force on loop 2, then
View SolutionThe magnetic field in a region is given by →B=B0(1+xa)ˆk. A square loop of edge length 'd' is placed with its edge along X-axis and Y-axis. The loop is moved with a constant velocity →V=V0ˆi. The emf induced in the loop is
View SolutionThe magnetic flux across a loop of resistance 10Ω is given by ϕ=5t2−4t+1Wb. How much current is induced in the loop after 0.2 s?
View Solution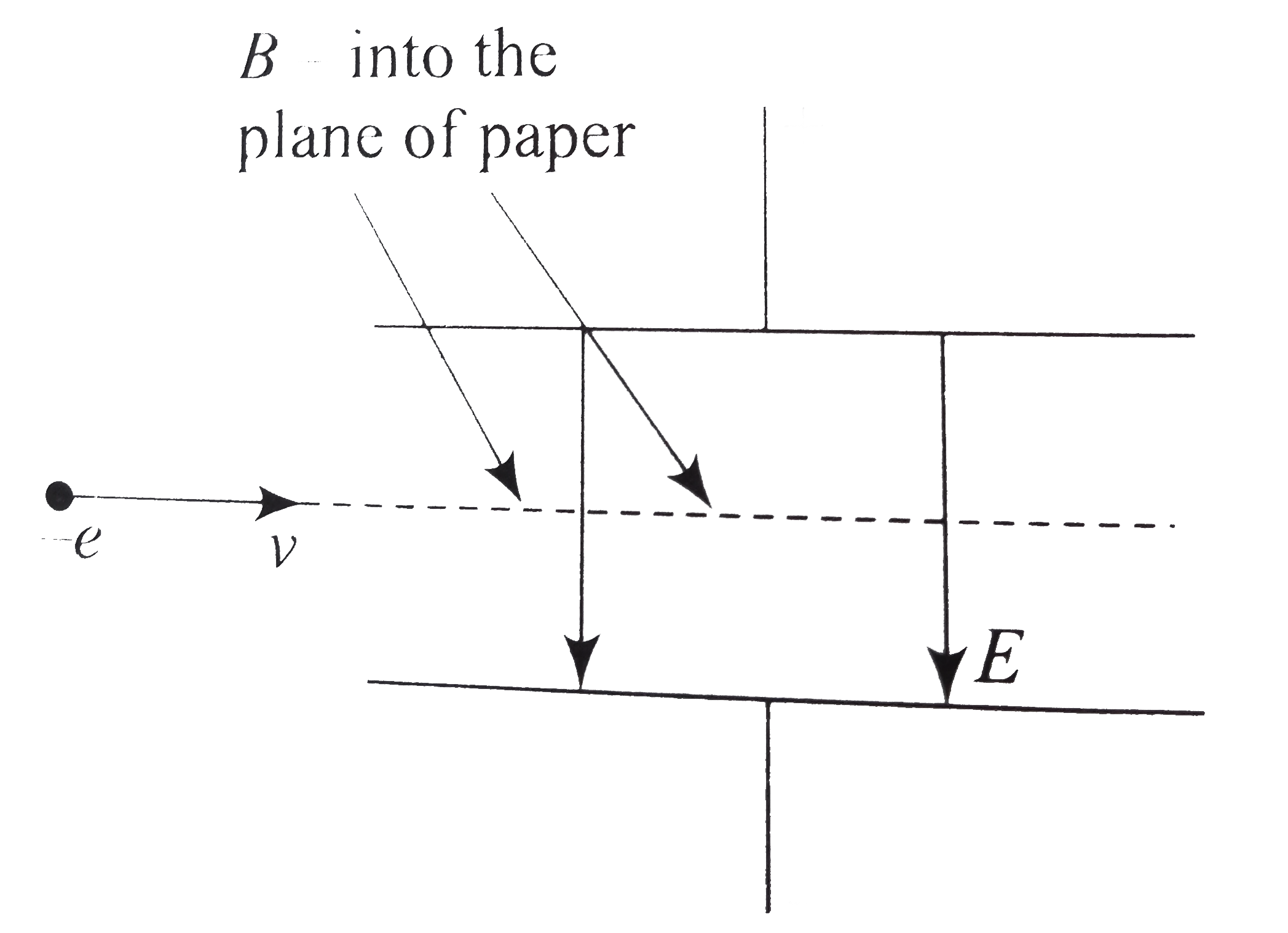
Electrons taveling at a velocity of 2.4×106ms−1 enter a region of crossed electric and magnetic fields as shoen in Fig. If the electric field is 3.0×106 Vm and the flux density of the magnetic field is 1.5 T, the electrons upon entering the region of the crossed fields will
View SolutionIn a region of space, the electric field is given by →E=8ˆi+4ˆj+3ˆk. The electric flux through a surface of area 100 units in the xy plane is
View SolutionThe magnetic field B due to a current- carrying circular loop of radius 12cm at its center is 0.50×(10−4)T. Find the magnetic field due to this loop at a point on the axis at a distance of 5.0 cm from the centre.
View SolutionThe magnetic field B due to a current- carrying circular loop of radius 12cm at its center is 0.50×(10−4)T. Find the magnetic field due to this loop at a point on the axis at a distance of 5.0 cm from the centre.
View Solution