Find the angle of the flint glass prism which should be combined with a crown glass prism of so as to give dispersion but no deviation.
For crown glass,
For flit glass,
To solve the problem of finding the angle of the flint glass prism that should be combined with a crown glass prism of 6∘ to achieve dispersion without deviation, we can follow these steps:
Step 1: Understand the Concept of Deviation
In optics, the deviation of light passing through a prism is determined by the refractive index of the material and the angle of the prism. For no deviation, the total deviation from both prisms must equal zero.
Step 2: Calculate the Mean Refractive Index
We first calculate the mean refractive index for both the crown glass and flint glass prisms.
For crown glass:
μc=μv+μr2=1.520+1.4802=3.0002=1.500
For flint glass:
μf=μv+μr2=1.780+1.7202=3.5002=1.750
Step 3: Set Up the Deviation Equation
The deviation (δ) for a prism can be expressed as:
δ=(μ−1)A
where A is the angle of the prism.
For the crown glass prism:
δc=(μc−1)Ac=(1.500−1)×6∘=0.500×6∘=3∘
For the flint glass prism, let the angle be Af:
δf=(μf−1)Af=(1.750−1)Af=0.750Af
Step 4: Set the Total Deviation to Zero
Since we want no net deviation, we set the deviations equal:
δf+δc=0
Substituting the expressions we found:
0.750Af−3∘=0
This implies:
0.750Af=3∘
Step 5: Solve for Af
Now, we can solve for Af:
Af=3∘0.750=4∘
Conclusion
The angle of the flint glass prism should be 4∘.
---
In optics, the deviation of light passing through a prism is determined by the refractive index of the material and the angle of the prism. For no deviation, the total deviation from both prisms must equal zero.
We first calculate the mean refractive index for both the crown glass and flint glass prisms.
μc=μv+μr2=1.520+1.4802=3.0002=1.500
μf=μv+μr2=1.780+1.7202=3.5002=1.750
The deviation (δ) for a prism can be expressed as:
δ=(μ−1)A
where A is the angle of the prism.
δc=(μc−1)Ac=(1.500−1)×6∘=0.500×6∘=3∘
δf=(μf−1)Af=(1.750−1)Af=0.750Af
Since we want no net deviation, we set the deviations equal:
δf+δc=0
Substituting the expressions we found:
0.750Af−3∘=0
This implies:
0.750Af=3∘
Now, we can solve for Af:
Af=3∘0.750=4∘
The angle of the flint glass prism should be 4∘.
Topper's Solved these Questions
- RAY OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - Example
21 Videos
- RAY OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - PRACTICE EXERCISE-1
1 Videos
- QUIZBOOK - VMC MODULES ENGLISHCHAPTER - QUIZEXERCISE - PHYSICS
30 Videos
- RAY OPTICS AND WAVE OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS AND WAVE OPTICS EXERCISE - IMPECCABLE
58 Videos
Similar Questions
A prism of crown glass having angle of refractive as 3∘ and refractive index = 1.51 is combined with one flint glass prism of refractive index = 1.65 to produce dispersion without deviation. Find the angle of flint glass and net dispersion.
Given,
μv=1.523,μR=1.513 (for crown glass)
μ'v=1.665,μ'R=1.645 (for flint glass)
View SolutionA combination of two prisms, one of flint and other of crown glass produces dispersion without deviation. The angle of flint glass prism is 15∘. Calculate the angle of crown glass prism and angular separation of red and violet rays on emergence from the spectroscope. (μ for crown glass =1.52,μ for flint glass =1.65,ω for crown glass =0.02,ω for flint glass =0.03).
View SolutionA crown glass prism of refracting angle 6∘ is to be used for deviation without dispersion with a flint glass of angle of prism α . Given : for crown glass μr=1.513andμv=1.523, for flint glass μr=1.645andμv=1.665. Find α
View SolutionCalculate the dispersive power (in multiple of 10−3 of crown glass-prism from the following data for crown glass (μv=1.503,μr=1.497)
View SolutionCalculate the dispersive power for crown glass from the given data
μv=1.523 and μr=1.5145.
View SolutionCalculate the dispersive power for crown glass from the given data
μv=1.523 and μr=1.5145.
View SolutionThe refractive indices of the crown glass for violet and red lights are1.51and 1.49respectively and those of the flint glass are1.77and1.73respectively A prism of angle 6∘is made of crown glass .A beam of white light is incident at a small angle on this prism.The other thin flint glass prism is combined white the crown glass prism such that te net mean deviation is1.5∘anticlockwise.
(i)Determine the angle of the flint glass prism.
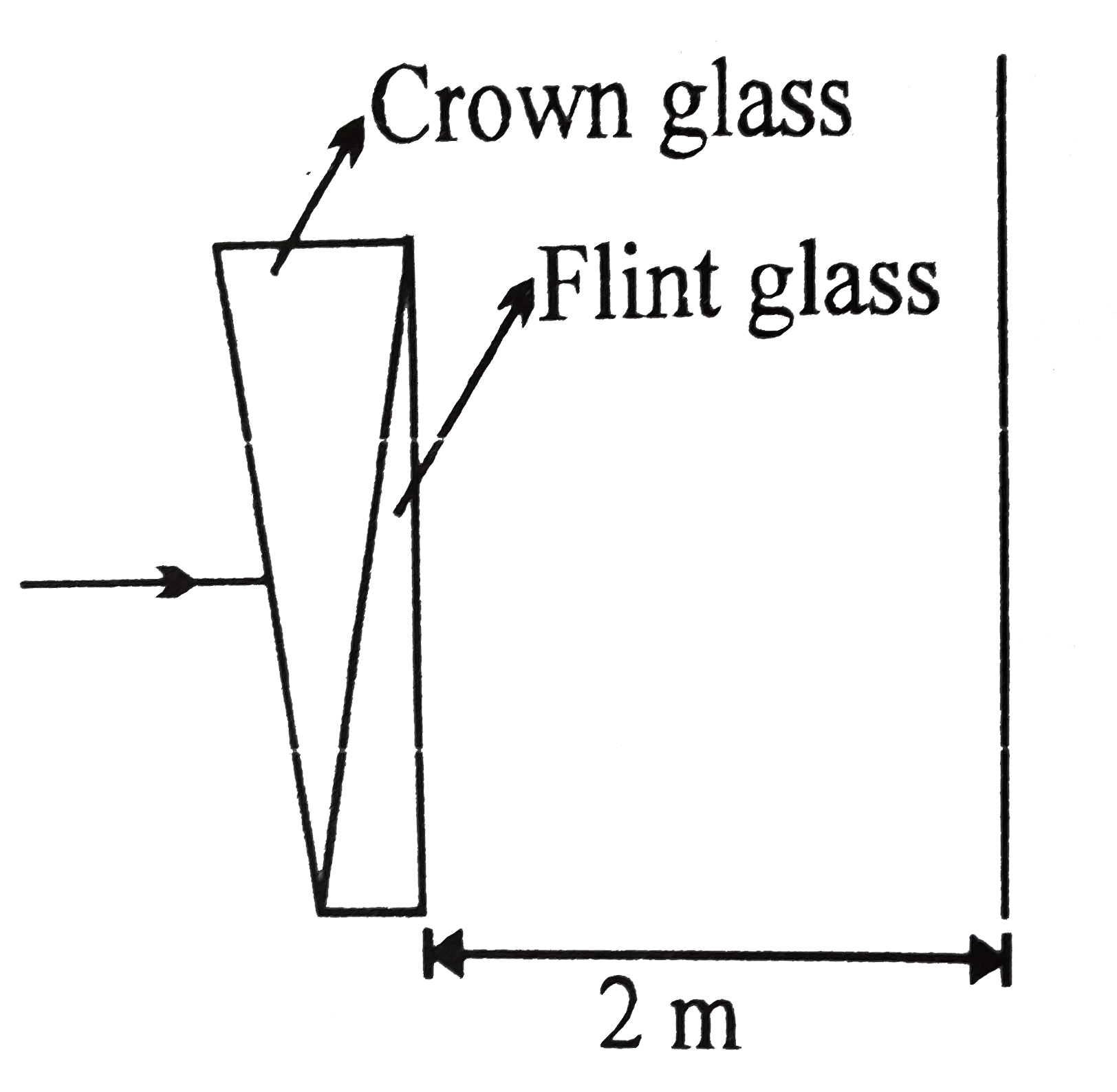
(ii)A screen is placed normal to the emerging beam at a distance of2mfrom the prism combination.find the distance between red and violet spot on the screen Which is the topmost colour on screen.
View SolutionFind the maximum angle of refraction when a light ray is refracted from glass (μ=1.50) to air.
View SolutionA crown glass prism of refracting angle 8∘ is combined with a flint glass prism to obtain deviation without dispersion. If the refractive indicates for red and violet rays for the crown glass are 1.514 and 1.524 and for the flint glass are 1.645 and 1.665 respectivey, find the angle of flint glass prism and net deviation.
View SolutionA prism of crown glass with refracting angle of 5∘ and mean refractive index = 1.151 is combined with a flint glass prism of refractive index = 1.65 to produce deviation. Find the angle of fliint glass.
View Solution
