Find the maximum angle of refraction when a light ray is refracted from glass (μ=1.50) to air.
To find the maximum angle of refraction when a light ray is refracted from glass (with a refractive index μ=1.50) to air, we can follow these steps:
Step 1: Understand the concept of critical angle
The critical angle is the angle of incidence in the denser medium (glass) at which the angle of refraction in the less dense medium (air) is 90 degrees. Beyond this angle, total internal reflection occurs.
Step 2: Use Snell's Law
Snell's Law relates the angles of incidence and refraction to the refractive indices of the two media. It is given by the formula:
μ1sin(θ1)=μ2sin(θ2)
where:
- μ1 is the refractive index of the first medium (glass, μ1=1.50),
- θ1 is the angle of incidence,
- μ2 is the refractive index of the second medium (air, μ2≈1.00),
- θ2 is the angle of refraction.
Step 3: Set the angle of refraction to 90 degrees
For the maximum angle of refraction, we set θ2=90∘. Thus, we can rewrite Snell's Law as:
μ1sin(θ1)=μ2sin(90∘)
Since sin(90∘)=1, this simplifies to:
μ1sin(θ1)=μ2
Step 4: Substitute the known values
Substituting the values into the equation:
1.50sin(θ1)=1.00
Step 5: Solve for sin(θ1)
Rearranging the equation gives:
sin(θ1)=1.001.50=23
Step 6: Calculate θ1
Now, we find θ1:
θ1=arcsin(23)
Step 7: Determine the maximum angle of refraction
The maximum angle of refraction θ2 is 90 degrees, which occurs when the angle of incidence θ1 is equal to the critical angle.
Conclusion
Thus, the maximum angle of refraction when a light ray is refracted from glass to air is 90∘.
---
The critical angle is the angle of incidence in the denser medium (glass) at which the angle of refraction in the less dense medium (air) is 90 degrees. Beyond this angle, total internal reflection occurs.
Snell's Law relates the angles of incidence and refraction to the refractive indices of the two media. It is given by the formula:
μ1sin(θ1)=μ2sin(θ2)
where:
- μ1 is the refractive index of the first medium (glass, μ1=1.50),
- θ1 is the angle of incidence,
- μ2 is the refractive index of the second medium (air, μ2≈1.00),
- θ2 is the angle of refraction.
For the maximum angle of refraction, we set θ2=90∘. Thus, we can rewrite Snell's Law as:
μ1sin(θ1)=μ2sin(90∘)
Since sin(90∘)=1, this simplifies to:
μ1sin(θ1)=μ2
Substituting the values into the equation:
1.50sin(θ1)=1.00
Rearranging the equation gives:
sin(θ1)=1.001.50=23
Now, we find θ1:
θ1=arcsin(23)
The maximum angle of refraction θ2 is 90 degrees, which occurs when the angle of incidence θ1 is equal to the critical angle.
Thus, the maximum angle of refraction when a light ray is refracted from glass to air is 90∘.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXAMPLE9videos
GEOMETRICAL OPTICS
- BOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer18videos
GEOMETRICAL OPTICS
- BOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Objective -27videos
GEOMETRICAL OPTICS
- BOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Short Question7videos
GAUSS LAW
- BOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer11videos
LIGHT WAVES
Similar Questions
Find the angle θa made by the light ray when it gets refracted from water to air, as shown in Fig .
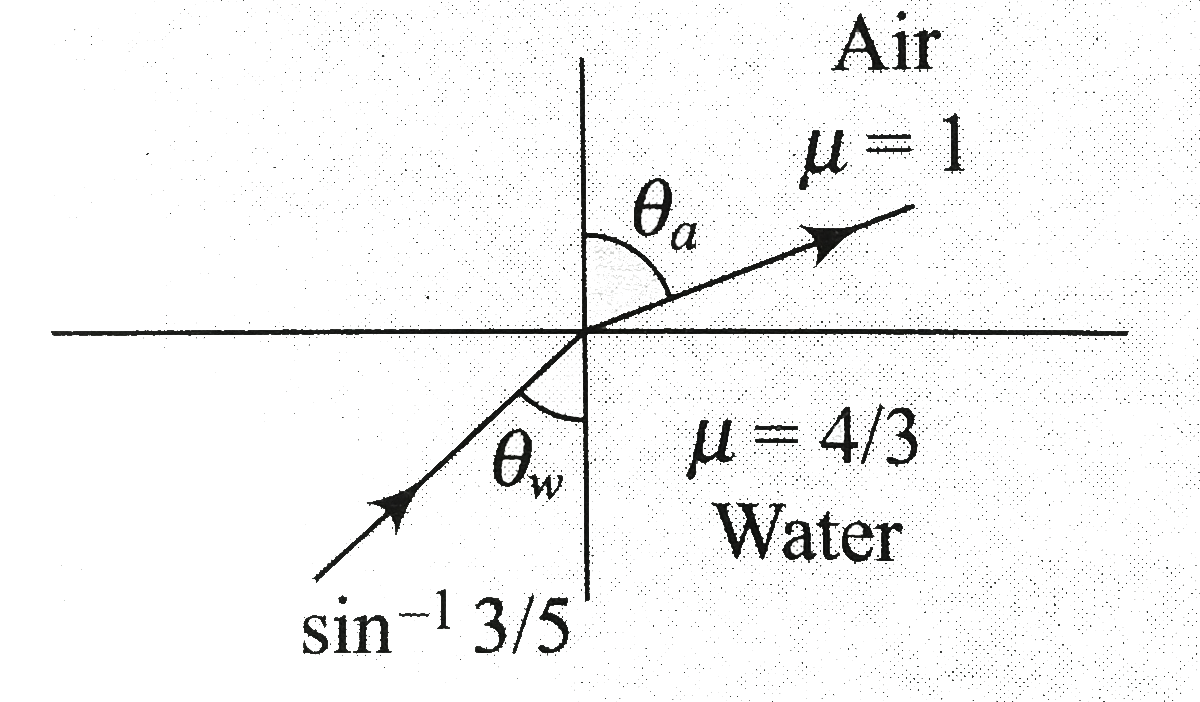 View Solution
View SolutionThe angle of incidence is always smaller than angle of refraction when a ray travels from air to glass. ______
View SolutionA circular beam of light of diameter (width) falls on a plane surface of glass. The angle of incidence is .I., angle of refraction is .r. and refractive index of glass is μ. Then the diameter of the refracted beam d. is…….
View SolutionA plane wavefront is incident at an angle of 37∘ with horizontal a boundary of refractive medium from air (μ=1) to a medium of refractive index μ=32. Find the angle of refracted wavefront with horizontal
View SolutionFind the angle of deviation suffered by the light ray shown in figure. The refractive index μ=2.0 for the prism material.
View SolutionCalculate the critical angle of glass and water pair. (The refractive index for glass is 1.50 and refractive index for water is 1.33).
View SolutionAnswer the following:
(a) Define wavefront. Use Huygens' principle to verify the laws of refraction.
(b) How is linearly polarised light obtained by the process of scattering of light? Find the Brewster angle for air-glass interface, when the refractive index of glass is 1.5 .View SolutionFig. (a) and (b) show refraction of an incident ray in air at 60∘ with the normal to a glass-air and water-air interface respectively. Predict the angle of refraction of an incident ray in water at 45∘ with the normal to a water glass interface. Take .aμg=1.32.
 .View Solution
.View SolutionFind the angle of devaition suffered by the light ray shown in figure for following two conditions. The refractive index for the prism material is μ=3/2.
(i) When the prism is placed in air 9μ=1)
(ii) When the prism is placed in water (μ=4/3)
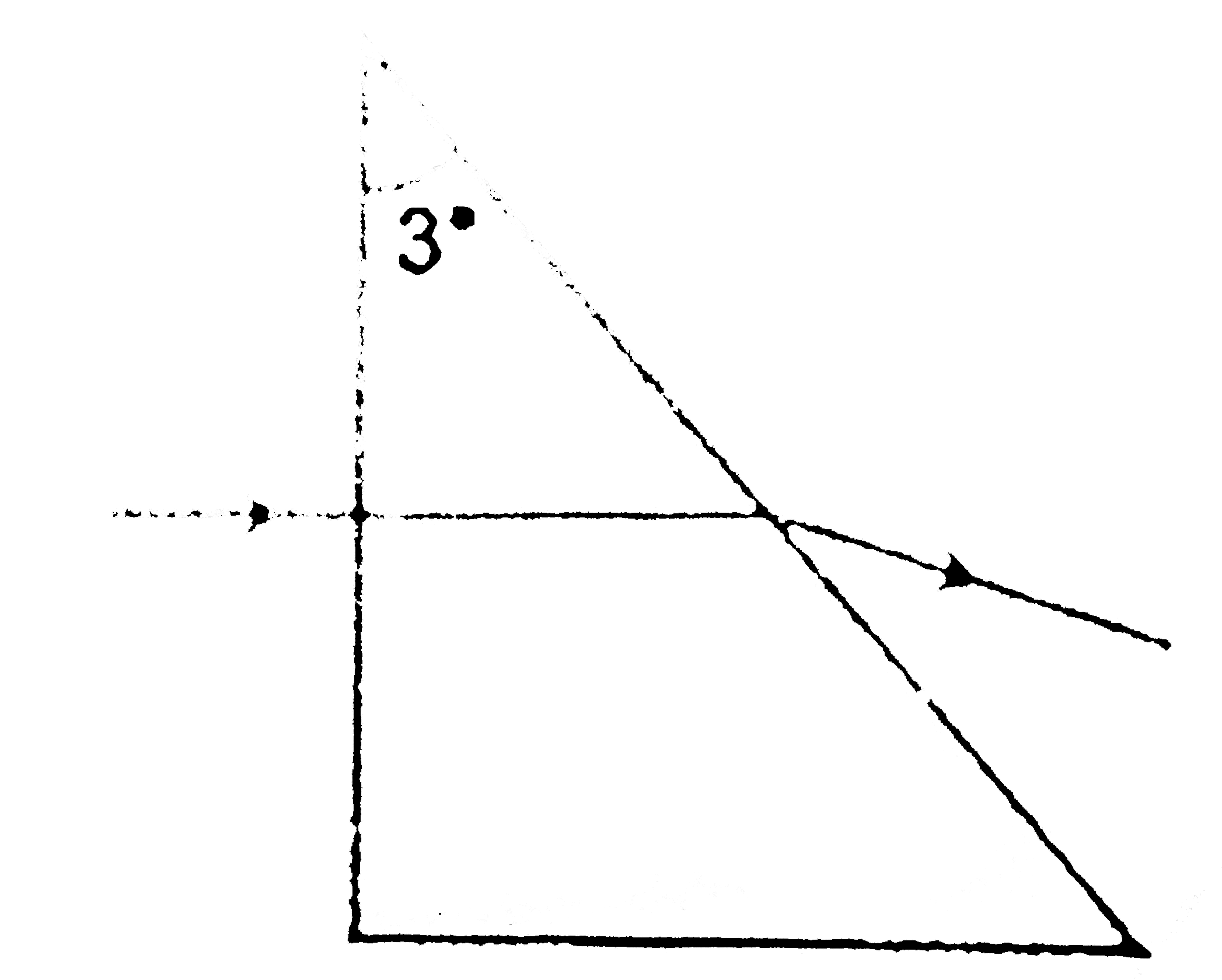 View Solution
View SolutionA ray of light is incident on the hypotenuse of a right-angled prism after travelling parallel to the base inside the prism. If μ is the refractive index of the material of the prism, the maximum value of the base angle for which light is totally reflected from the hypotenuse is
View Solution

