The rate expression for the reaction A(g) + B(g) C(g) is rate = . What changes in the initial concentration of A and B will cause the rate of reaction increase by a factor of eight?
The correct Answer is:B
To determine how the initial concentrations of A and B can be changed to increase the rate of the reaction by a factor of eight, we start with the given rate expression:
Rate Expression:
Rate=k(CA)2(CB)1/2
Where:
- (CA) is the concentration of A,
- (CB) is the concentration of B,
- k is the rate constant.
Step 1: Understand the current rate expression
The rate of the reaction is dependent on the concentrations of A and B raised to their respective powers in the rate law.
Step 2: Define the initial rate
Let the initial concentrations of A and B be (CA) and (CB). The initial rate R0 can be expressed as:
R0=k(CA)2(CB)1/2
Step 3: Determine the new rate for an increase by a factor of 8
To increase the rate by a factor of 8, we want:
R=8R0
Step 4: Set up the equation for the new concentrations
Let the new concentrations of A and B be (C′A) and (C′B). The new rate can be expressed as:
R=k(C′A)2(C′B)1/2
Step 5: Relate the new rate to the initial rate
We want:
k(C′A)2(C′B)1/2=8k(CA)2(CB)1/2
This simplifies to:
(C′A)2(C′B)1/2=8(CA)2(CB)1/2
Step 6: Consider possible changes in concentrations
Now we can analyze the changes in concentrations. We can express (C′A) and (C′B) in terms of their initial concentrations:
1. Let (C′A)=x(CA)
2. Let (C′B)=y(CB)
Substituting these into the equation gives:
(x(CA))2(y(CB))1/2=8(CA)2(CB)1/2
This simplifies to:
x2y1/2(CA)2(CB)1/2=8(CA)2(CB)1/2
Step 7: Cancel out the common terms
Since (CA)2(CB)1/2 is common on both sides, we can cancel it out:
x2y1/2=8
Step 8: Solve for x and y
Now we need to find values of x and y that satisfy this equation.
1. If we double the concentration of A, x=2:
(2)2y1/2=8
4y1/2=8
y1/2=2
y=4
Thus, if we double the concentration of A and quadruple the concentration of B, the rate will increase by a factor of 8.
Conclusion
The concentrations of A and B should be changed as follows:
- Double the concentration of A: (C′A)=2(CA)
- Quadruple the concentration of B: (C′B)=4(CB)
Rate=k(CA)2(CB)1/2
- (CA) is the concentration of A,
- (CB) is the concentration of B,
- k is the rate constant.
The rate of the reaction is dependent on the concentrations of A and B raised to their respective powers in the rate law.
Let the initial concentrations of A and B be (CA) and (CB). The initial rate R0 can be expressed as:
R0=k(CA)2(CB)1/2
To increase the rate by a factor of 8, we want:
R=8R0
Let the new concentrations of A and B be (C′A) and (C′B). The new rate can be expressed as:
R=k(C′A)2(C′B)1/2
We want:
k(C′A)2(C′B)1/2=8k(CA)2(CB)1/2
(C′A)2(C′B)1/2=8(CA)2(CB)1/2
Now we can analyze the changes in concentrations. We can express (C′A) and (C′B) in terms of their initial concentrations:
1. Let (C′A)=x(CA)
2. Let (C′B)=y(CB)
(x(CA))2(y(CB))1/2=8(CA)2(CB)1/2
x2y1/2(CA)2(CB)1/2=8(CA)2(CB)1/2
Since (CA)2(CB)1/2 is common on both sides, we can cancel it out:
x2y1/2=8
Now we need to find values of x and y that satisfy this equation.
(2)2y1/2=8
4y1/2=8
y1/2=2
y=4
The concentrations of A and B should be changed as follows:
- Double the concentration of A: (C′A)=2(CA)
- Quadruple the concentration of B: (C′B)=4(CB)
Similar Questions
The rate expression for reaction A(g)+B(g)→C(g) is rate =k[A]1/2[B]2. What change in rate if initial concentration of A and B increases by factor 4 and 2 respectively ?
View SolutionIn the reaction 2A+B→A2B, Rate = k[A]^2 [ B ] if the concentration of A is doubled and that of B is halved, then the rate of reaction will:
View SolutionConsider the reaction, A+B→C+D.
The initial rate for different initial concentrations of the reactants are given below :
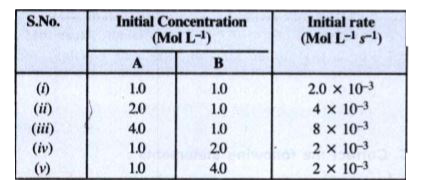
Write the rate law equation.
View SolutionConsider the reaction, A+B→C+D.
The initial rate for different initial concentrations of the reactants are given below :

Write the rate law equation.
View SolutionConsider the reaction, A+B→C+D.
The initial rate for different initial concentrations of the reactants are given below :

Write the rate law equation.
View SolutionConsider the reaction, A+B→C+D.
The initial rate for different initial concentrations of the reactants are given below :
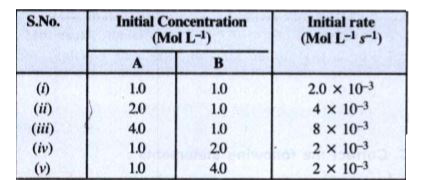
Calculate the rate constant.
View SolutionConsider the reaction, A+B→C+D.
The initial rate for different initial concentrations of the reactants are given below :

Calculate the rate constant.
View SolutionConsider the reaction, A+B→C+D.
The initial rate for different initial concentrations of the reactants are given below :

Calculate the rate constant.
View SolutionFor a hypothetical reaction, A+B→C+D, the rate =k[A]−1/2[B]3/2. On doubling the concentration of A and B the rate will be
View SolutionIn a reaction between A and B, the initial rate of reaction was measured for different initial concentrations of A and B as given below:
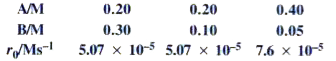
What is the order of reaction with respect to A and B ?
View Solution
