Rate law for the elementary reaction will be:
Rate =
Rate =
Rate =
Rate =
The correct Answer is:C
To determine the rate law for the elementary reaction 2ABk1−→A2+B2, we can follow these steps:
Step 1: Identify the Reaction
The given reaction is 2ABk1−→A2+B2. This indicates that two moles of AB react to form one mole of A2 and one mole of B2.
Hint: Look at the stoichiometry of the reactants and products to understand the relationship between them.
Step 2: Understand Elementary Reactions
An elementary reaction is a reaction that occurs in a single step. For elementary reactions, the rate law can be directly derived from the stoichiometry of the reaction.
Hint: Remember that for elementary reactions, the molecularity is equal to the order of the reaction.
Step 3: Determine Molecularity
In this reaction, there are 2 moles of AB on the reactant side. Therefore, the molecularity of this reaction is 2.
Hint: Count the number of reactant molecules involved in the elementary step to find the molecularity.
Step 4: Write the Rate Law
Since the molecularity is 2, the rate law can be expressed in terms of the concentration of the reactant AB. The rate law is given by:
Rate=k1(AB)n
where n is the molecularity of the reaction. Here, n=2.
Hint: Use the molecularity to determine the exponent in the rate law expression.
Step 5: Final Rate Law Expression
Substituting n=2 into the rate law expression, we get:
Rate=k1(AB)2
This means the rate of the reaction is proportional to the square of the concentration of AB.
Hint: Ensure that you include the rate constant k1 and the correct concentration term in your final expression.
Conclusion
Thus, the rate law for the elementary reaction 2ABk1−→A2+B2 is:
Rate=k1(AB)2
The given reaction is 2ABk1−→A2+B2. This indicates that two moles of AB react to form one mole of A2 and one mole of B2.
An elementary reaction is a reaction that occurs in a single step. For elementary reactions, the rate law can be directly derived from the stoichiometry of the reaction.
In this reaction, there are 2 moles of AB on the reactant side. Therefore, the molecularity of this reaction is 2.
Since the molecularity is 2, the rate law can be expressed in terms of the concentration of the reactant AB. The rate law is given by:
Substituting n=2 into the rate law expression, we get:
Thus, the rate law for the elementary reaction 2ABk1−→A2+B2 is:
Similar Questions
The differential rate law equation for the elementary reaction A+2Bk−−→3C, is
View SolutionFor the elementary reaction, A+2B→C, the rate law will be equal to :-
View SolutionIf the concentration of the reactants in the elementary reaction 2A + B → C + D is increased three folds, the rate of the reaction will be increased by:
View SolutionFor a hypotherical elementary reaction
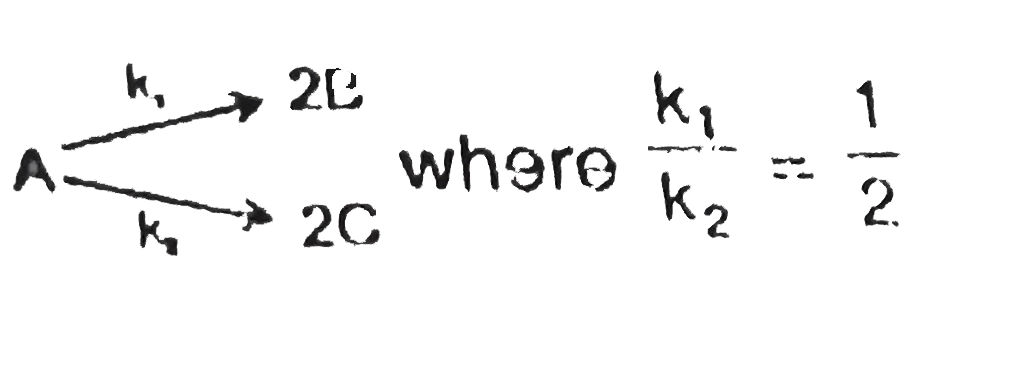 where k1k2=12
where k1k2=12
Initailly only 2 moles of A are present.
Number of moles of B are , if reactions gets 50 % completed :
View SolutionFor a hypotherical elementary reaction
 where k1k2=12
where k1k2=12
Initailly only 2 moles of A are present.
The total number of moles A,B and C at the end of 50% reaction are :
View SolutionFor a hypotherical elementary reaction
 where k1k2=12
where k1k2=12
Initailly only 2 moles of A are present.
The sum of mole of (B) are ( C) at end of reaction is :
View SolutionWrite the rate law and order for the following reaction:
AB2+C2→AB2C+C (slow)
AB2+C→AB2C( fast)
View SolutionWrite the rate law and order for the following reaction:
AB2+C2→AB2C+C (slow)
AB2+C→AB2C( fast)
View SolutionWrite the rate law and order for the following reaction:
AB2+C2→AB2C+C (slow)
AB2+C→AB2C( fast)
View SolutionThe rate law for the chemical reaction 2NO2Cl→2NO2+Cl2+Cl2=k[NO2Cl] is rate The rate determining step is
View Solution
