kt+10/k1 is known as:
Ratio of equilibrium constants
Temperature coefficient
Difference in temperature of reversible reactions
None of these
The correct Answer is:B
To solve the question regarding the expression kT+10kT, we will follow these steps:
Step 1: Understand the Variables
- Here, kT represents the rate constant at a certain temperature T.
- kT+10 represents the rate constant at a temperature that is 10 degrees higher than T.
Step 2: Identify the Relationship
- The relationship between the rate constants at different temperatures can be expressed using the temperature coefficient θ.
- The temperature coefficient θ is defined as the factor by which the rate constant changes when the temperature is increased by 10 degrees Celsius.
Step 3: Use the Temperature Coefficient Formula
- The formula relating the rate constants at two temperatures is given by:
kT+10kT=θΔT/10
- In this case, ΔT=10 (since we are increasing the temperature by 10 degrees).
Step 4: Substitute the Values
- Substitute ΔT=10 into the equation:
kT+10kT=θ10/10=θ1=θ
Step 5: Conclusion
- Therefore, kT+10kT is equal to θ, which is known as the temperature coefficient.
Final Answer
Thus, kT+10kT is known as the temperature coefficient.
---
- Here, kT represents the rate constant at a certain temperature T.
- kT+10 represents the rate constant at a temperature that is 10 degrees higher than T.
- The relationship between the rate constants at different temperatures can be expressed using the temperature coefficient θ.
- The temperature coefficient θ is defined as the factor by which the rate constant changes when the temperature is increased by 10 degrees Celsius.
- The formula relating the rate constants at two temperatures is given by:
kT+10kT=θΔT/10
- In this case, ΔT=10 (since we are increasing the temperature by 10 degrees).
- Substitute ΔT=10 into the equation:
kT+10kT=θ10/10=θ1=θ
- Therefore, kT+10kT is equal to θ, which is known as the temperature coefficient.
Thus, kT+10kT is known as the temperature coefficient.
Similar Questions
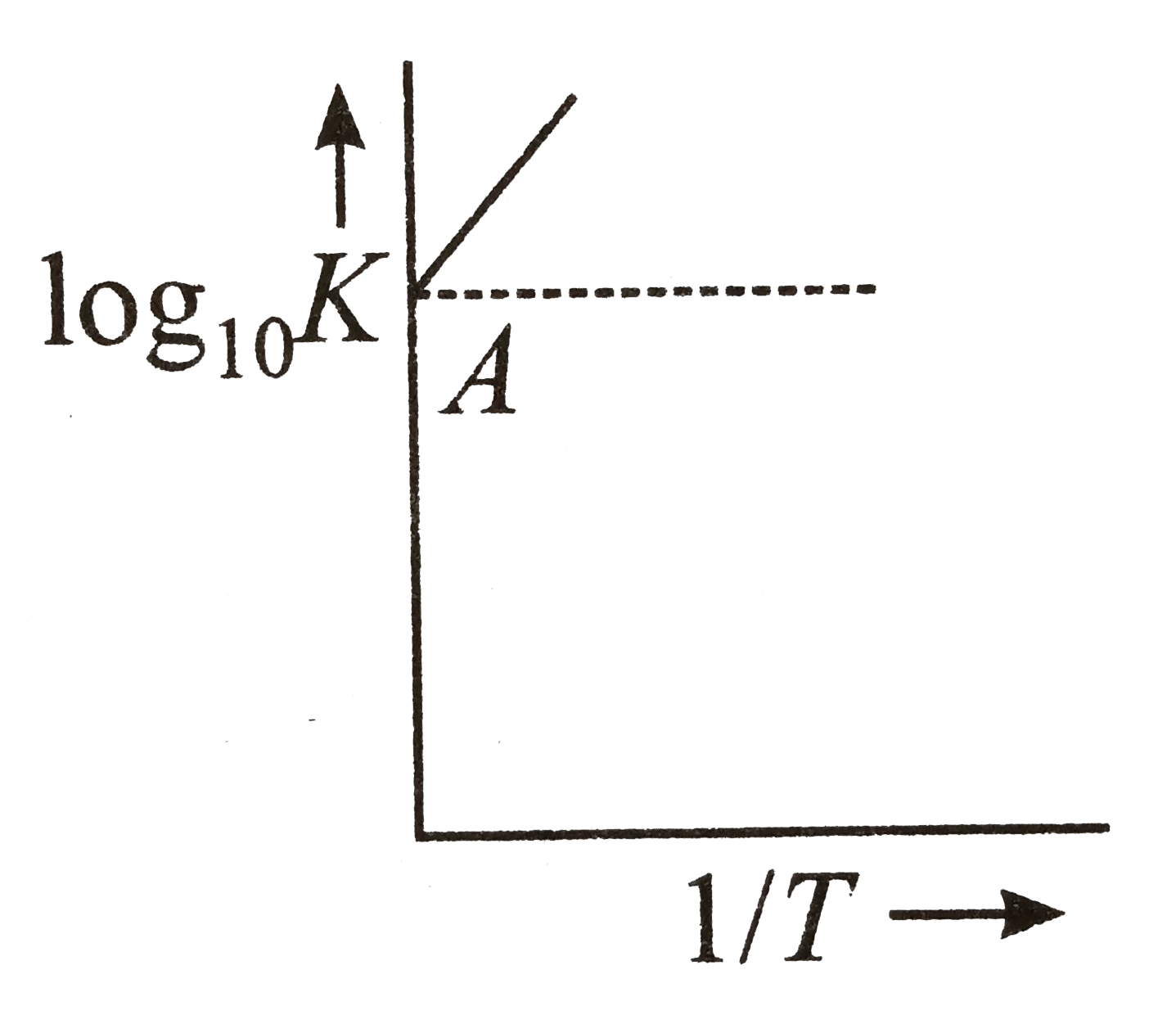
Variation of log10K with 1T is shown by the following graph in which straight line is at 45∘ , hence ΔH∘ is:
View SolutionVariation of equilibrium constan K with temperature is given by van't Hoff equation
InK=ΔrS∘R−ΔrH∘RT
for this equation, (ΔrH∘) can be evaluated if equilibrium constans K1 and K2 at two temperature T1 and T2 are known.
log(K2K1)=ΔrH∘2.303R[1T1−1T2]
Variation of log10 K with 1T is shown by the following graph in which straight line is at 45∘ hence ΔH∘ is :
View SolutionVariation of equilibrium constan K with temperature is given by van't Hoff equation
InK=ΔrS∘R−ΔrH∘RT
for this equation, (ΔrH∘) can be evaluated if equilibrium constans K1 and K2 at two temperature T1 and T2 are known.
log(K2K1)=ΔrH∘2.303R[1T1−1T2]
Select the correct statement :
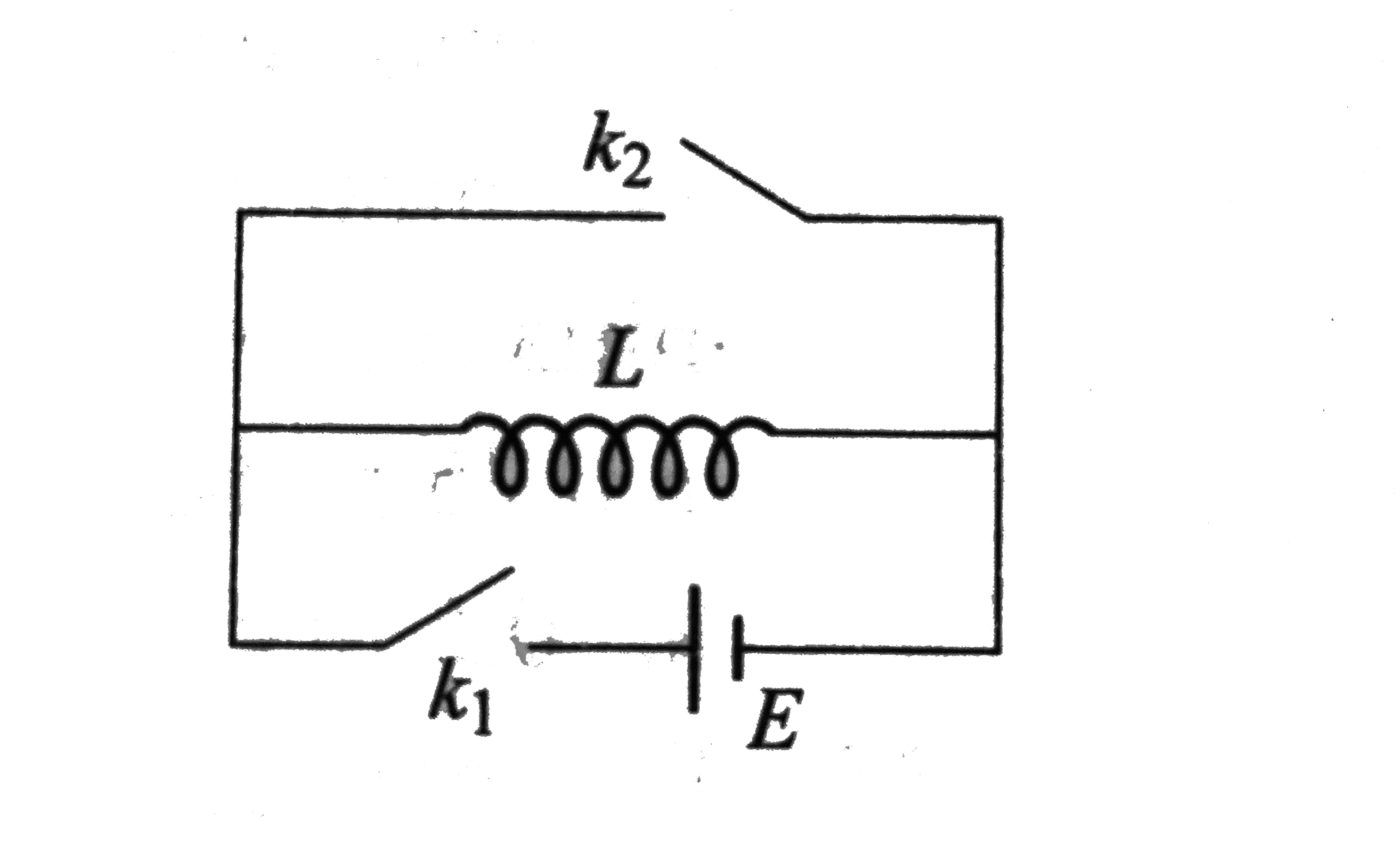
View SolutionIn the circuit shows in Fig. switch k2 is open and switch k1 is closed at t=0. At time t=t0, switch k1 is opened and switch k2 is simultaneosuly closed. The variation of inductor current with time is
View SolutionStatement 1 1,2,4,8,….. is a GP,4,8,16,32,…. is a GP and 1+4,2+8,4+16,8+32,…. is also a GP. Statement 2 Let general term of a GP with common ratio r be Tk+1 and general term of another GP with common ratio r be T'k+1, then the series whode general term T''k+1=Tk+1+T'k+1 is also a GP woth common ratio r.
View SolutionA circuit containing capacitors C1 and C2 as shown in the figure are in steady state with key K1 closed.At the instant t=0, if K1 is opened and K2 is closed then the maximum current in the circuit will be:

View SolutionA circuit containing capacitors C1andC2 shown in Fig. is in the steady state with key K1 closed. At the instant t = 0, K1 is opened and K2 is closed. The angular frequency of oscillation of the circuit is
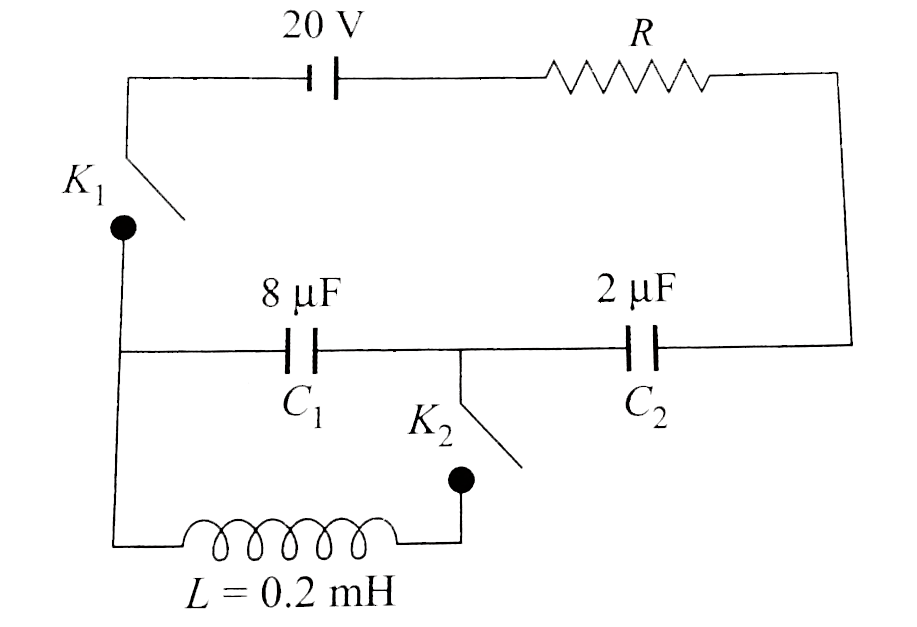
View SolutionThe value of the expression (10∑r=010Cr)(10∑k=0(−1)k^10Ck2k) is :
View SolutionA=⎡⎢⎣10k213k01⎤⎥⎦ is invertible for
View SolutionIn the equation (1pβ)=ykBT, where p is the pressure, y is the distance, kB is Boltzmann constant and T is the tempreture. Dimensions of β are
View Solution
