What will be the work done by external agent to slowly hang the lower end of the chain to the peg?
−MgL2
MgL2
−MgL4
MgL4
The correct Answer is:D
To find the work done by an external agent to slowly hang the lower end of a chain to a peg, we can follow these steps:
Step 1: Understand the System
We have a chain of mass m and length L. The chain is initially hanging vertically, and we need to hang the lower end of the chain to a peg, which will change the configuration of the chain.
Step 2: Identify the Initial and Final States
- Initial State: The entire chain is hanging down. The center of mass of the chain is at a height of L2 from the ground.
- Final State: When the lower end of the chain is attached to the peg, the chain will form a "U" shape. The center of mass of the chain will be at a height of 3L4 from the ground.
Step 3: Calculate the Initial Potential Energy
The potential energy (PE) of the chain when it is fully hanging is given by:
PEinitial=mghinitial=mg(L2)=mgL2
Step 4: Calculate the Final Potential Energy
When the lower end is hung to the peg, the center of mass of the chain is at a height of 3L4:
PEfinal=mghfinal=mg(3L4)=3mgL4
Step 5: Calculate the Change in Potential Energy
The work done by the external agent is equal to the change in potential energy:
W=PEfinal−PEinitial
Substituting the values:
W=3mgL4−mgL2
Step 6: Simplify the Expression
To simplify, we need a common denominator:
mgL2=2mgL4
Thus,
W=3mgL4−2mgL4=mgL4
Conclusion
The work done by the external agent to slowly hang the lower end of the chain to the peg is:
mgL4
We have a chain of mass m and length L. The chain is initially hanging vertically, and we need to hang the lower end of the chain to a peg, which will change the configuration of the chain.
- Initial State: The entire chain is hanging down. The center of mass of the chain is at a height of L2 from the ground.
- Final State: When the lower end of the chain is attached to the peg, the chain will form a "U" shape. The center of mass of the chain will be at a height of 3L4 from the ground.
The potential energy (PE) of the chain when it is fully hanging is given by:
PEinitial=mghinitial=mg(L2)=mgL2
When the lower end is hung to the peg, the center of mass of the chain is at a height of 3L4:
PEfinal=mghfinal=mg(3L4)=3mgL4
The work done by the external agent is equal to the change in potential energy:
W=PEfinal−PEinitial
Substituting the values:
W=3mgL4−mgL2
To simplify, we need a common denominator:
mgL2=2mgL4
Thus,
W=3mgL4−2mgL4=mgL4
The work done by the external agent to slowly hang the lower end of the chain to the peg is:
mgL4
Topper's Solved these Questions
- MOCK TEST 3BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 3EXERCISE - PART I : PHYSICS (SECTION-2)
10 Videos
- MOCK TEST 2BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 2EXERCISE - PART I : PHYSICS (SECTION - 2)
10 Videos
- MOCK TEST 4BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 4EXERCISE - PHYSICS (SECTION 2)
5 Videos
Similar Questions
The gravitational field in a region is given by →E=(10Nkg−1)(→i+→j). Find the work done by an external agent to slowly shift a particle of mass 2 kg from the point (0,0) to a point (5m,4m)
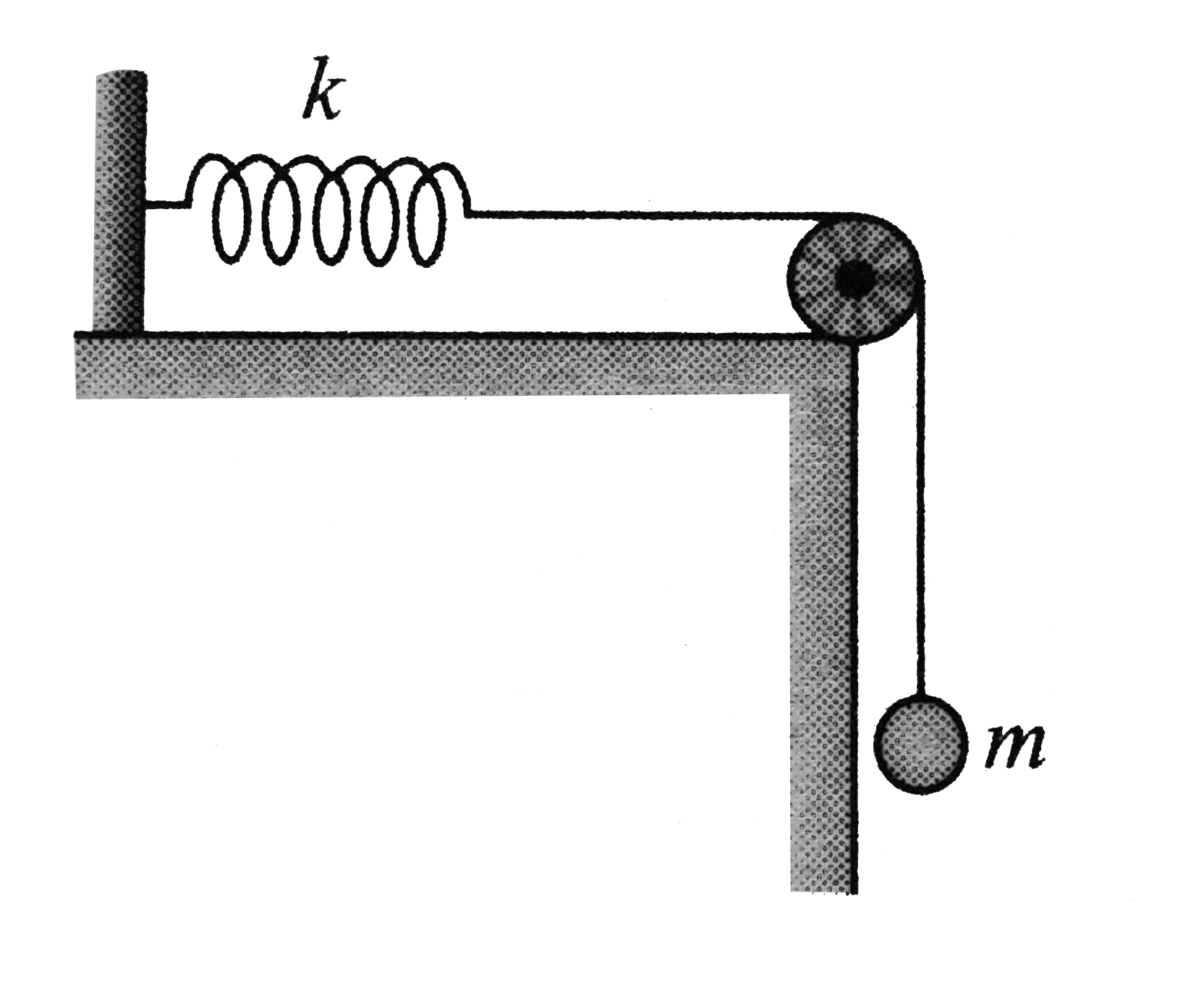
View SolutionIn figure, the light spring is of force constant k and is on a smooth horizontal surface. Initially the spring is relaxed. Calculate the work done by an external agent to lower the hanging body of mass M slowly, till it remains in equilibrium.
View SolutionA man places a chain (of mass m and length l) on a table slowly. Initially, the lower end of the chain just touches the table. The main brings down the chain by length l/2. Work done by the man in this process is
View Solutionfind the work done by an external agent in slowly shifting a charge q=1μC in the electric field →E=103ˆiVm−1 from the point P(1,2)toQ(3,4).
View SolutionA body of mass 2 kg is moved from a point A to a point B by an external agent in a conservative force field. If the velocity of the body at the points A and B are 5m/s and 3m/s respectively and the work done by the external agent is - 10 J, then the change in potential energy between point A and B is
View SolutionA planet of mass M has uniform density in a spherical volume of radius R. Calculate the work done by the external agent to deassemble the planet in eight identical spherical part against gravitational pull amongst its constitute particle.
View SolutionConsider the configuration of a system of four charges each of value (+q). Find the work done by external agent in changing the configuration of the system from (Fig. 3.44 A) to (Fig. 3.4B).
a. ,
,
View SolutionA point charge q0 is moved slowly from the centre of a ring R, ( that is carrying a charge q) to a distance x from its centre along its axis. What is the work done by the external agent in this process ?
Strategy : According to work energy theorem, if there is no change in kinetic energy, we have
Wext+WE=0
⇒Wext=−WE
=−q0(VA−VB)
View SolutionA charge is moved in an electric field of a fixed charge distribution from point A to another point B slowly. The work done by external agent in doing so is 100J . What is the change in potential energy of the charge as it moves from A to B ? What is the work done by the electric field of the charge distribution as the charge moves from A to B ?
View SolutionA charge is moved in an electric field of a fixed charge distribution from point A to another point B slowly. The work done by external agent in doing so is 100J. What is the change in potential energy of the charge as it moves from A to B ? What is the work done by the electric field of the charge distribution as the charge moves from A to B ?
View Solution
