How many roots foes the following equation possess $3^{| x |} (| 2 - | x ∣ ∣) = 2$ ?

A

1

B

2

C

3

D

4

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

We have,
$3^{| x |} {2 - | x |} = 1$ ..........(i)
$\Rightarrow 2 - | x | = 3^{- | x |}$
In order to determine the number of roots of (i), it is sufficient to find the points of intersection of the curves $y = 2 - | x |$ and $y = 3^{- | x |}$ . Graphs of these two curves are shown in Fig.2.

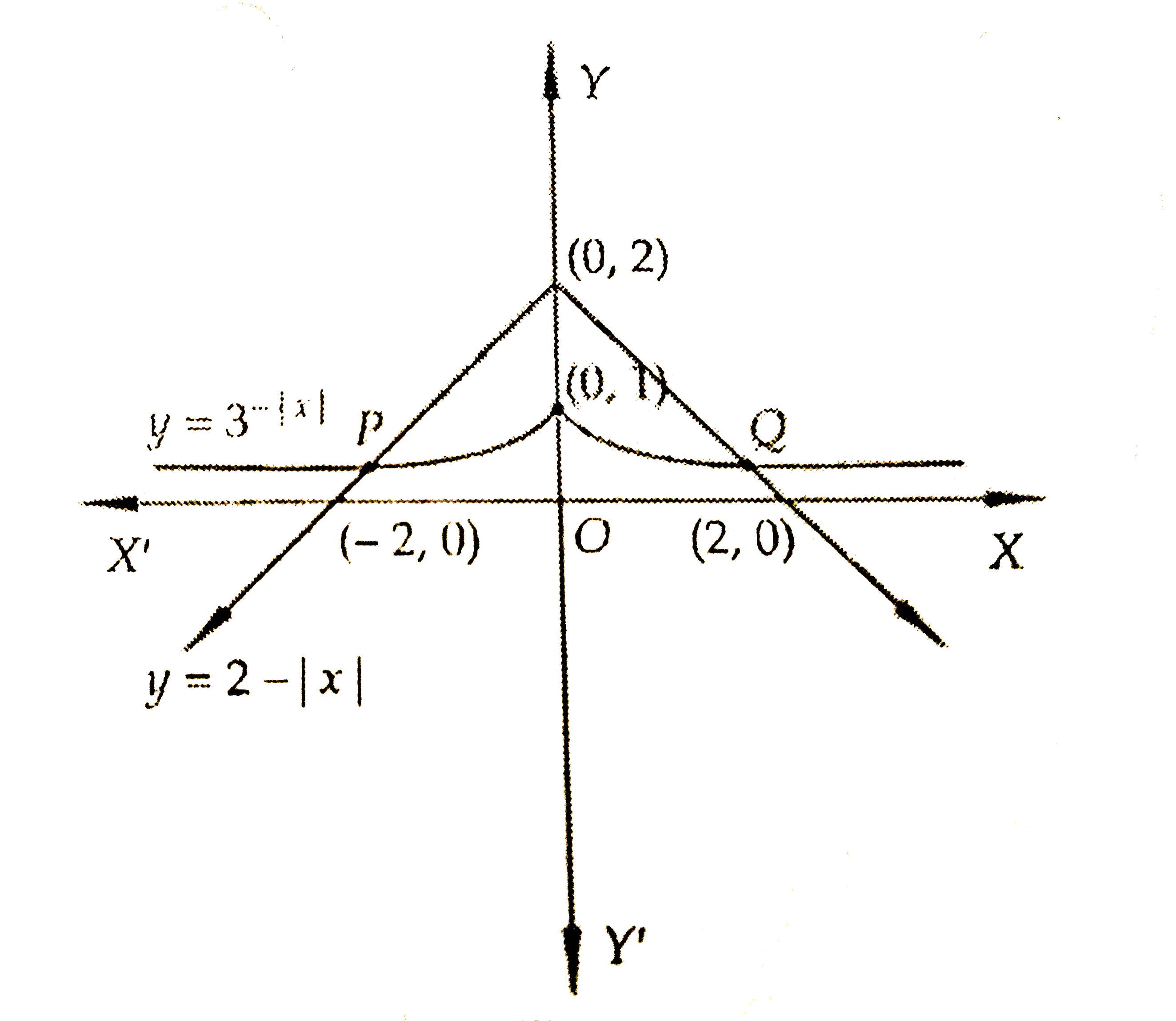
We observe that the two curves intersect at two points P and Q. Hence, the equation (i) has two real solutions. Also the solutions belong to the interval (-2,2).

|

Updated on:21/07/2023

Class 12 MATHS MISCELLANEOUS EQUATIONS AND INEQUATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
How many solutions exist to the equation $| x | = | 2 x - 1 |$ ?
A $0$
B $1$
C $2$
D $3$

OBJECTIVE RD SHARMA ENGLISH-MISCELLANEOUS EQUATIONS AND INEQUATIONS -Chapter Test

Home
Ask Doubt
Profile