Question

The number of real solutions of the equation ${\log }_{a}x=\left|x\right|,0<a<1$, is

Options

A. 0
B. 1
C. 2
D. None of these

Answer

B

Explanation

The number of real solutions of the equation `log_(a)x=|x|` is equal to the number of points of intersection of the curves
`y=log_(a)` x and `y=|x|`
The graphs of these two curves are shown in Fig.3.

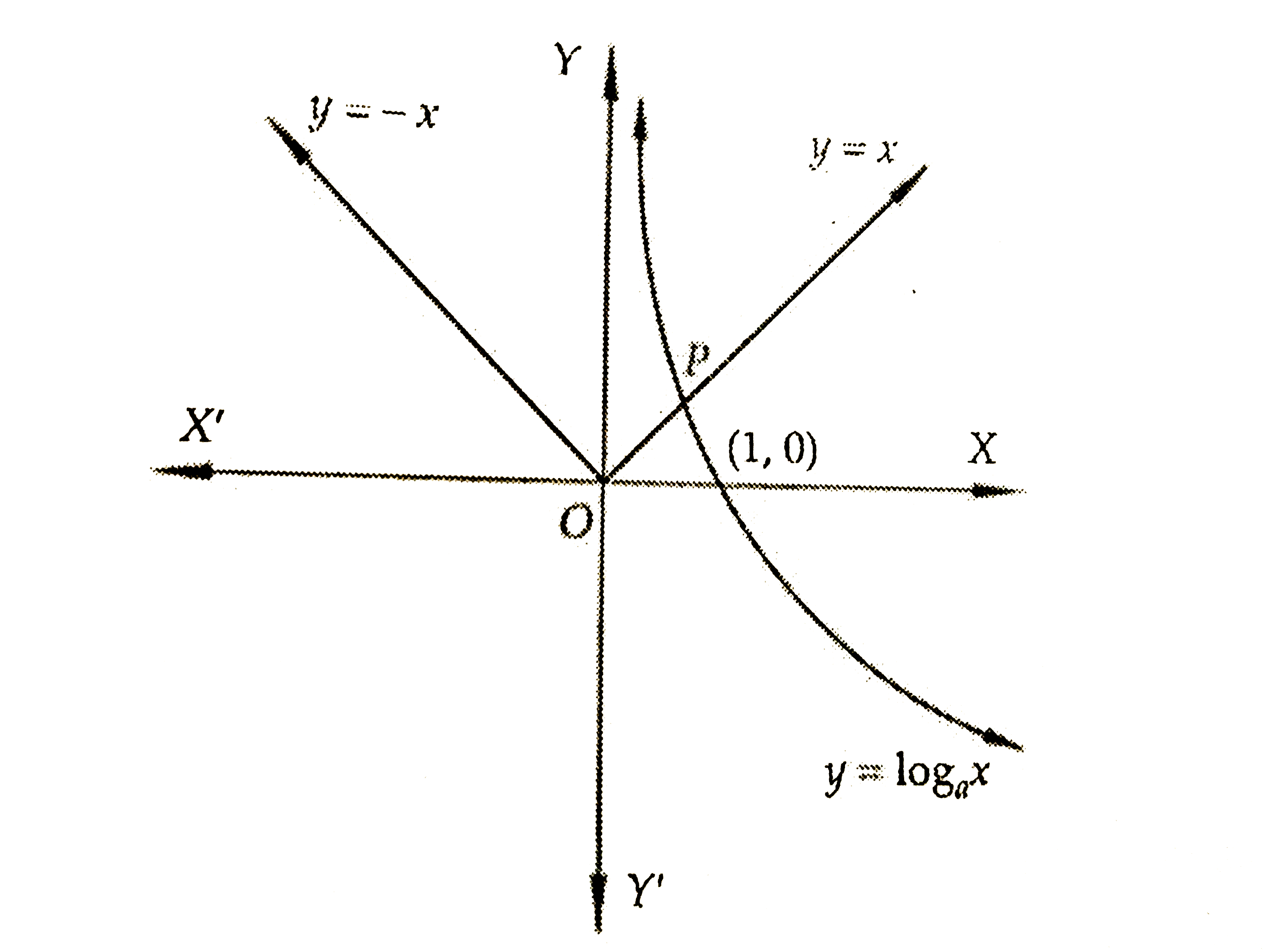
It is evident the graph that the two curves intersect at one point only. Hence, the given equation has one real solution lying between 0 and 1.