If then the solution set for
{2}
[0,2]
The correct Answer is:C
To solve the inequality 5x+(2√3)2x≥13x, we will follow these steps:
Step 1: Rewrite the inequality
We start with the given inequality:
5x+(2√3)2x≥13x
We can rewrite (2√3)2x as 4⋅3x:
5x+4⋅3x≥13x
Step 2: Divide by 13x
Next, we divide the entire inequality by 13x (assuming 13x>0):
5x13x+4⋅3x13x≥1
This simplifies to:
(513)x+4(313)x≥1
Step 3: Define a function
Let f(x)=(513)x+4(313)x. We need to find when f(x)≥1.
Step 4: Evaluate the function at specific points
1. Evaluate at x=1:
f(1)=(513)1+4(313)1=513+1213=1713>1
2. Evaluate at x=2:
f(2)=(513)2+4(313)2=25169+4⋅9169=25+36169=61169<1
3. Evaluate at x=3:
f(3)=(513)3+4(313)3=1252197+4⋅272197=125+1082197=2332197<1
Step 5: Determine the solution set
From the evaluations:
- f(1)>1
- f(2)<1
- f(3)<1
This indicates that f(x) is decreasing. Therefore, the solution set for the inequality f(x)≥1 is:
x≤1
Final Answer
The solution set for the inequality 5x+(2√3)2x≥13x is:
(−∞,1)
We start with the given inequality:
5x+(2√3)2x≥13x
We can rewrite (2√3)2x as 4⋅3x:
5x+4⋅3x≥13x
Next, we divide the entire inequality by 13x (assuming 13x>0):
5x13x+4⋅3x13x≥1
This simplifies to:
(513)x+4(313)x≥1
Let f(x)=(513)x+4(313)x. We need to find when f(x)≥1.
1. Evaluate at x=1:
f(1)=(513)1+4(313)1=513+1213=1713>1
f(2)=(513)2+4(313)2=25169+4⋅9169=25+36169=61169<1
f(3)=(513)3+4(313)3=1252197+4⋅272197=125+1082197=2332197<1
From the evaluations:
- f(1)>1
- f(2)<1
- f(3)<1
x≤1
The solution set for the inequality 5x+(2√3)2x≥13x is:
(−∞,1)
Topper's Solved these Questions
- MISCELLANEOUS EQUATIONS AND INEQUATIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MISCELLANEOUS EQUATIONS AND INEQUATIONS EXERCISE - Exercise
30 Videos
- MISCELLANEOUS EQUATIONS AND INEQUATIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MISCELLANEOUS EQUATIONS AND INEQUATIONS EXERCISE - Chapter Test
29 Videos
- MEASURES OF CENTRAL TENDENCYBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MEASURES OF CENTRAL TENDENCYEXERCISE - Chapter Test
21 Videos
- PLANE AND STRAIGHT LINE IN SPACE BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PLANE AND STRAIGHT LINE IN SPACE EXERCISE - Chapter Test
31 Videos
Similar Questions
Knowledge Check
If −5<2x−3≤x+2,x∈R, then the solution set of x on the number line is
A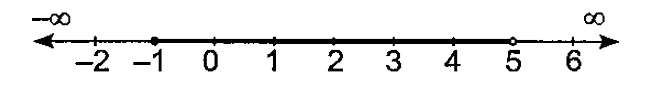 B
B C
C D
D
If 2≤2x−3≤5,x∈I, then the solution set of x on the number line is:
A B
B C
C D
D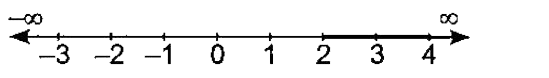
If 3−2x2>5x,x∈R , then the set of solutions is
AA. (−∞,−12)BB. (3,∞)CC. (−12,3)DD. [−12,3]
Solve √x−2≥−1.
View SolutionIf (0.2)2x−3x−2>5 then complete solution set of values of x is
View SolutionIf f(x)=2ln(x−2)−x2+4x+1, then find the solution set of the inequality f′(x)≥0
View SolutionIf f(x)=2ln(x−2)−x2+4x+1, then find the solution set of the inequality f′(x)≥0
View SolutionIf 2x−3≤x+1≤4x+7,x∈I (integers), then the solution set of x is
View Solution
