Question

(i) The positive value of k for which ${\displaystyle k{e}^x-x=0}$ has only one root is

Options

A. `(1)/(e )`
B. 1
C. e
D. log 2

Answer

A

Explanation

Consider the function `f(x)=ke^(x)-x`.
We have,
`f'(x)=ke^(x)-1`
`:. F'(x)=0 rArrke^(x)=1 rArr e^(x)=(1)/(k)rArrx=-logk`.
The signs of f' (x) for different values of x are as shown below.

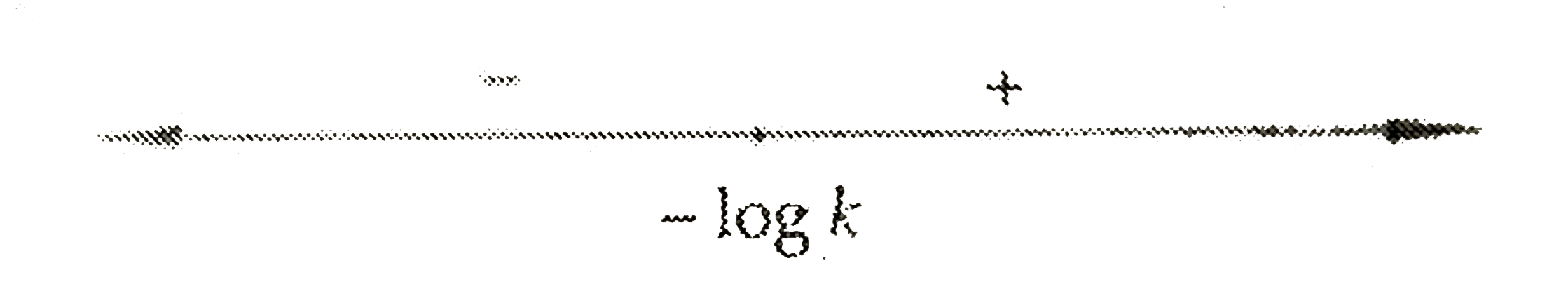
So, f(x) attains its minimum value at x=-logk
Also, the minimum value of f(x) is f(-logk)=1+logk.
Thus, f(x)=0 will have exactly one root if its minimum value 1+log k is zero.
i.e. `1+log k=0 rArr k=1//e`