If V=43πr3, at what rate in cubic units is V increasing when r = 10 and drdt = 0.01?
π
4π
40π
4π/3
The correct Answer is:B
To solve the problem, we need to find the rate at which the volume V is increasing when the radius r=10 and the rate of change of the radius drdt=0.01.
1. Write the formula for volume:
The volume V of a sphere is given by the formula:
V=43πr3
2. Differentiate the volume with respect to time:
To find the rate at which the volume is changing with respect to time, we need to differentiate V with respect to t:
dVdt=ddt(43πr3)
Using the chain rule, we have:
dVdt=43π⋅3r2⋅drdt
The 3 from the differentiation of r3 cancels with the 13 in front:
dVdt=4πr2⋅drdt
3. Substitute the known values:
Now we substitute r=10 and drdt=0.01 into the equation:
dVdt=4π(102)⋅0.01
Calculate 102:
102=100
Substitute this back into the equation:
dVdt=4π⋅100⋅0.01
4. Simplify the expression:
dVdt=4π⋅1=4π
5. Final answer with units:
Therefore, the rate at which the volume is increasing when r=10 is:
dVdt=4π cubic units
Summary:
The volume V is increasing at a rate of 4π cubic units when the radius r=10 and drdt=0.01.
The volume V of a sphere is given by the formula:
V=43πr3
To find the rate at which the volume is changing with respect to time, we need to differentiate V with respect to t:
dVdt=ddt(43πr3)
Using the chain rule, we have:
dVdt=43π⋅3r2⋅drdt
The 3 from the differentiation of r3 cancels with the 13 in front:
dVdt=4πr2⋅drdt
Now we substitute r=10 and drdt=0.01 into the equation:
dVdt=4π(102)⋅0.01
Calculate 102:
102=100
Substitute this back into the equation:
dVdt=4π⋅100⋅0.01
dVdt=4π⋅1=4π
Therefore, the rate at which the volume is increasing when r=10 is:
dVdt=4π cubic units
The volume V is increasing at a rate of 4π cubic units when the radius r=10 and drdt=0.01.
Topper's Solved these Questions
- DERIVATIVE AS A RATE MEASURER BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DERIVATIVE AS A RATE MEASURER EXERCISE - Exercise
26 Videos
- DERIVATIVE AS A RATE MEASURER BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DERIVATIVE AS A RATE MEASURER EXERCISE - Exercise
26 Videos
- DEFINITE INTEGRALSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DEFINITE INTEGRALSEXERCISE - Chapter Test 2
56 Videos
- DIFFERENTIAL EQUATIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Chapter Test
30 Videos
Similar Questions
The network shown in figure is a part of a complete circuit. If at a certain instant, the current i is 4 A and is increasing at a rate of 103A/S. ThenVB−VA will be
View SolutionIn the measurement of volume of solid sphere using the formula V=43πr3 if the error committed in the measurement of the radius r is 1.5%, the percentage error in the volume measurement is
View SolutionThe radius of a circle is increasing uniformly at the rate of 3 cm/s. Find the rate at which the area of the circle is increasing when the radius is 10 cm.
View SolutionIn an AC subcircuit as shown in figure, the resistance R=1omega. At a certain instant VA−VB=2V and current is increasing at the rate of dldt=10 As. The inductance of the coils is
_PHY_E06_299_Q01.png)
View SolutionIn the circuit (Fig.) what is potential difference VB−VA (in V) when current I is 5A and is decreasing at the rate of 103As−1
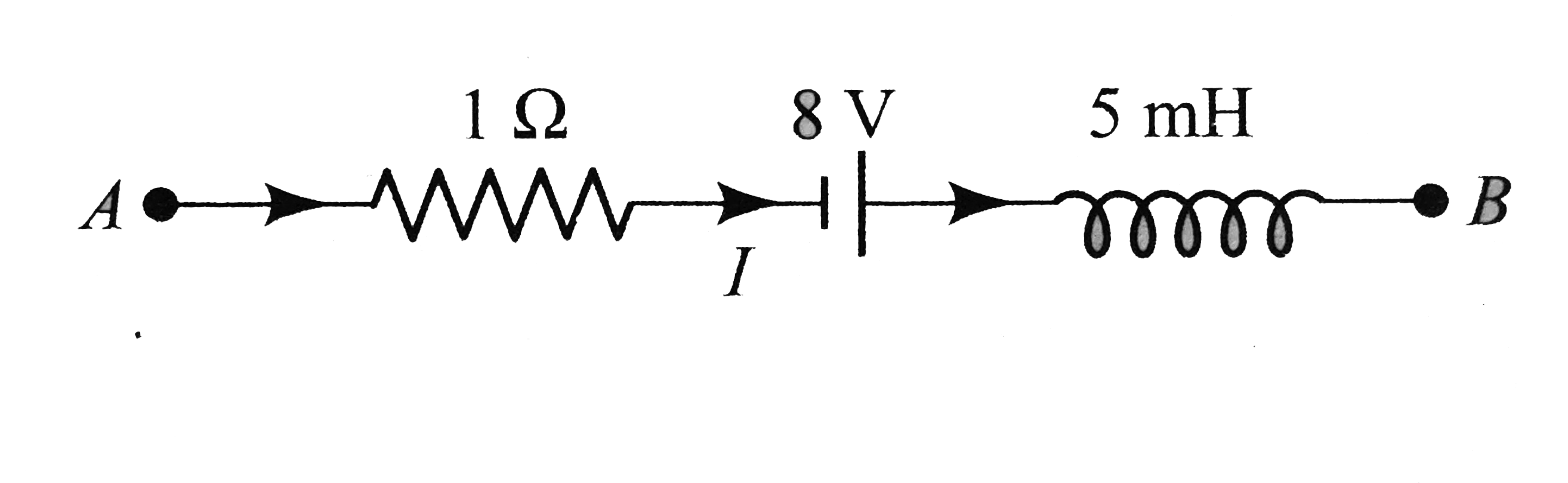
View Solution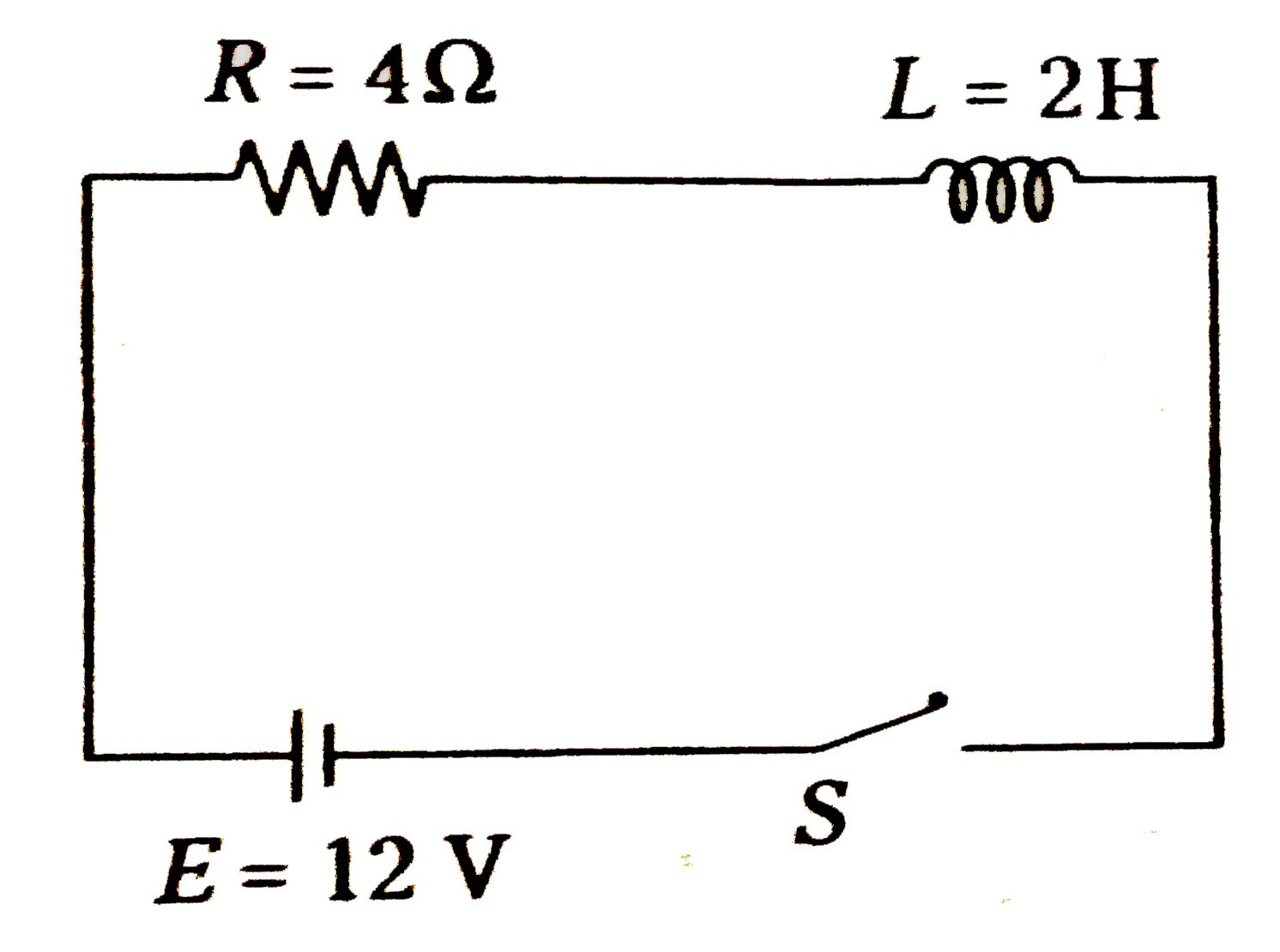
At t = 0, switch S is closed, calculate
(i) initial rate of increase of current, i.e., didtat t=0.
(ii) didt at time when current in the circuit is 0.5A.
(iii) Current at t = 0.6 s.
(iv) rate at which energy of magnetic field is increasing, rate of heat produced in resistance and rate at which energy is supplied by battery when i = 0.5 A.
(v) energy stored in inductor in steady state.
View SolutionIn the measurement of volume of solid sphere using the formula V=43πr3 if the error committed in the measurement of the radius r is 2%, the percentage error in the volume measurement is
View SolutionThe side of a square sheet of a metal is increasing at 3 cm per minute . At what rate is the area increasing when the side is 10 cm long ?
View SolutionRadius of a circle is increasing at rate of 3cm/sec Find the rate at which the area of circle is increasing at the instant when radius is 10 cm.
View SolutionA cylindrical tank of radius 10 m is being filled with wheat at the rate of 314 cubic metre per hour. Then the depth of the wheat is increasing at the rate of(A) 1 m/h (B) 0.1 m3/h (C) 1.1 m3/h (D) 0.5 m3/h
View Solution
