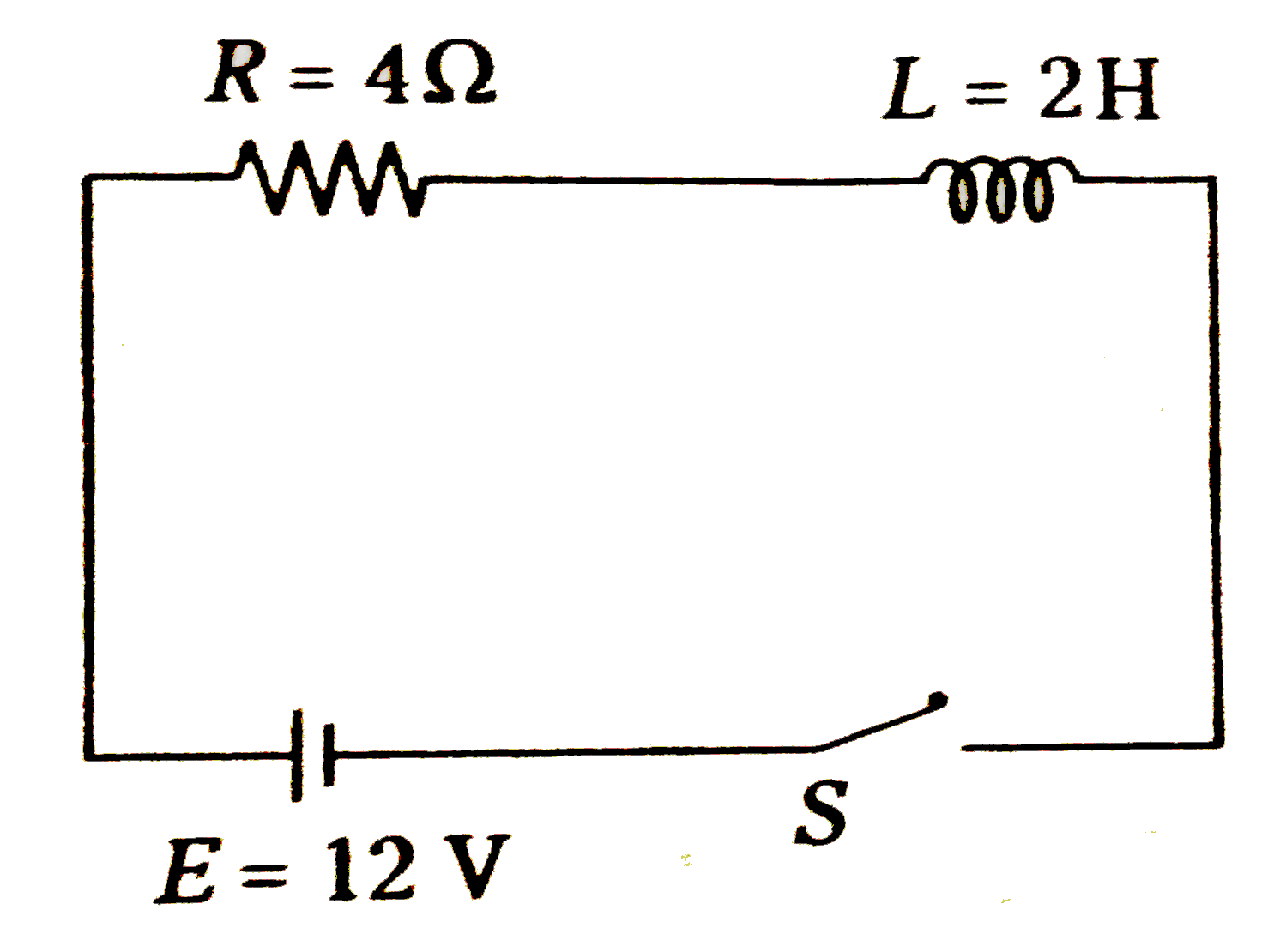
At t = 0, switch S is closed, calculate
(i) initial rate of increase of current, i.e., didtat t=0.
(ii) didt at time when current in the circuit is 0.5A.
(iii) Current at t = 0.6 s.
(iv) rate at which energy of magnetic field is increasing, rate of heat produced in resistance and rate at which energy is supplied by battery when i = 0.5 A.
(v) energy stored in inductor in steady state.
We know that
E=iR+L dt/dt
dtdt=E−iRL
Current in the circuit at any time t,
i=i0(1−e−t/τL)
where, i0=E/R,τL=L/R
(i) Rate of increase of current didt=E−iRL, when t = 0, i = 0
∣∣∣didt∣∣∣t=0=EL=122=6A/s
(ii) At t=0.5s,didt=E−iRL=12−0.5×42=12−22=5A/s
(iii) At t = 0.6 s, current i = ER(1−e−RtL)
=124(1−e4×0.60.5)=3(1−e2.4)A
(iv) Energy stored in inductor in steady state is given by
U=12Li2⇒dUdt=Lididt
didt=E−iRL=12−0.5×42=5A/s
dUdt=2×0.5×5=5J/s
Power produced per second, P=i2R=(0.5)2×4=1J/s
Power supplied by battery =Ei=0.5×12=6J/s
(v) We have i0=E/R=12/4=3A
Energy stored in inductor in steady state,
U=12Li20=12×2×(3)2=9J/s
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Check point
Explore 60 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Taking it together
Explore 119 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Level 2 Subjective
Explore 20 Videos
- CURRENT ELECTRICITYBook:DC PANDEY ENGLISHChapter:CURRENT ELECTRICITYExercise:Medical entrances gallery
Explore 97 Videos
- ELECTROMAGNETIC WAVESBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:Sec C
Explore 22 Videos
Similar Questions
Switch is closed at t=0 then the current in the circuit at t=L2R is
_PHY_E06_157_Q01.png)
View SolutionWhen the switch S, in the circuit shown, is closed, then the value of current I will be :
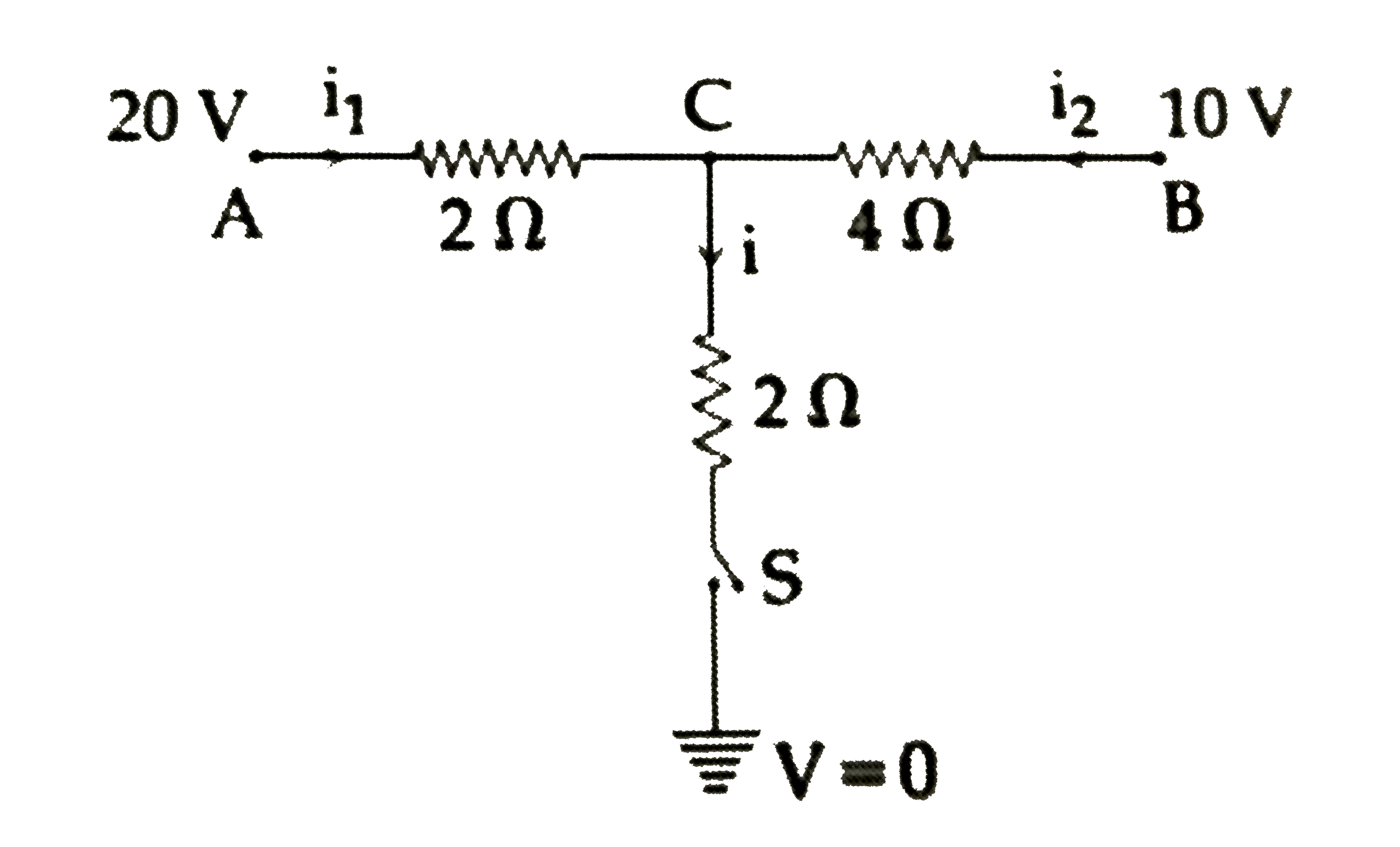
View SolutionIn the given at t=0, switch S is closed.
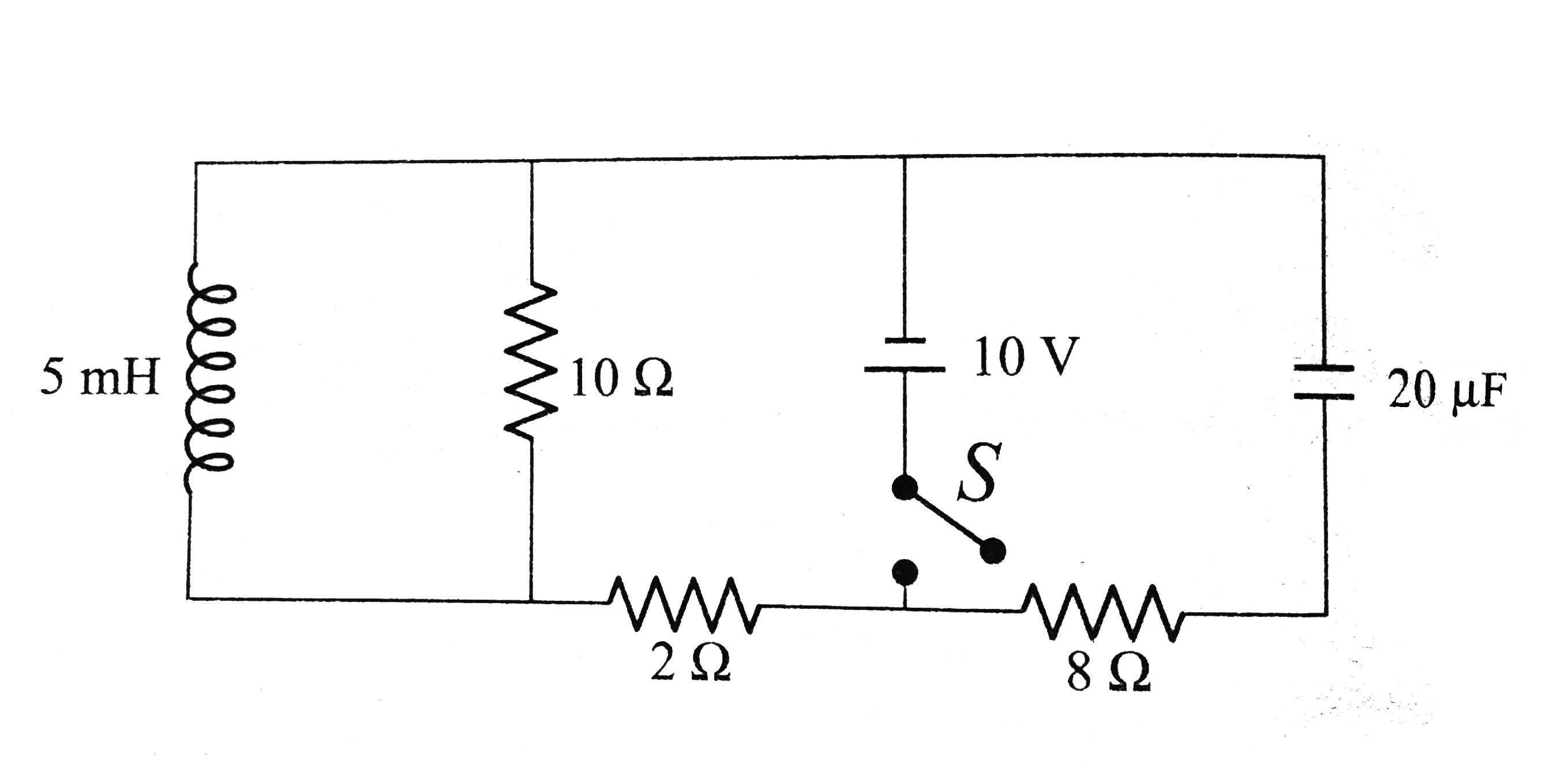
The energy stored in the inductor at any instant t(0<t∞) will be
View Solutionthere in no current part of this circuit for time t<o. Switch S is closed at t=0.

The rate at which the current through the inductor increases initially is
View SolutionA coil of inductance 1H and resistance 10Ω is connected to a resistanceless battery of emf 50V at time t=0. Calculate the ratio of rthe rate which magnetic energy is stored in the coil to the rate at which energy is supplied by the battery at t=0.1s.
View SolutionThe side of a square is increasing at the rate of 0.2 cm/s. The rate of increase of perimeter w.r.t time is :
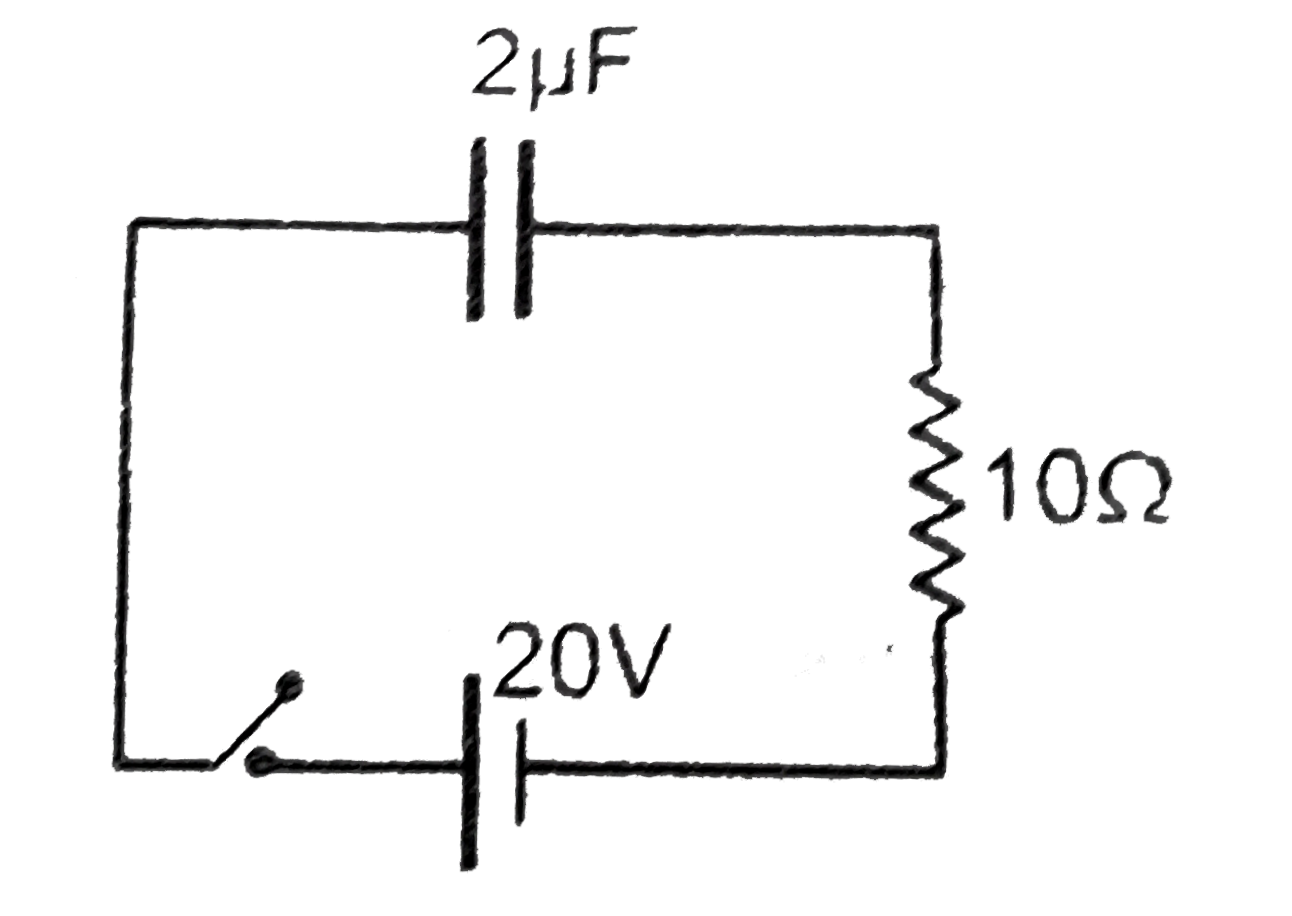
View SolutionInitially capacitor is uncharged at t=0 switch is closed. Charge on capacitor when current in the circuit is 10% of maximum current :
View SolutionAt the trophic level of consumers, the rate at which food energy is assimilarted, is called ?
View SolutionThe resistance of a coil is 5 ohm and a current of 0.2A is induced in it due to a varying magnetic field. The rate of change of magnetic flux in it will be-
View SolutionIn the following circuit (Fig.)the switch is closed at t=0. Intially, there is no current in inductor. Find out the equation of current in the inductor coil as s function of time.
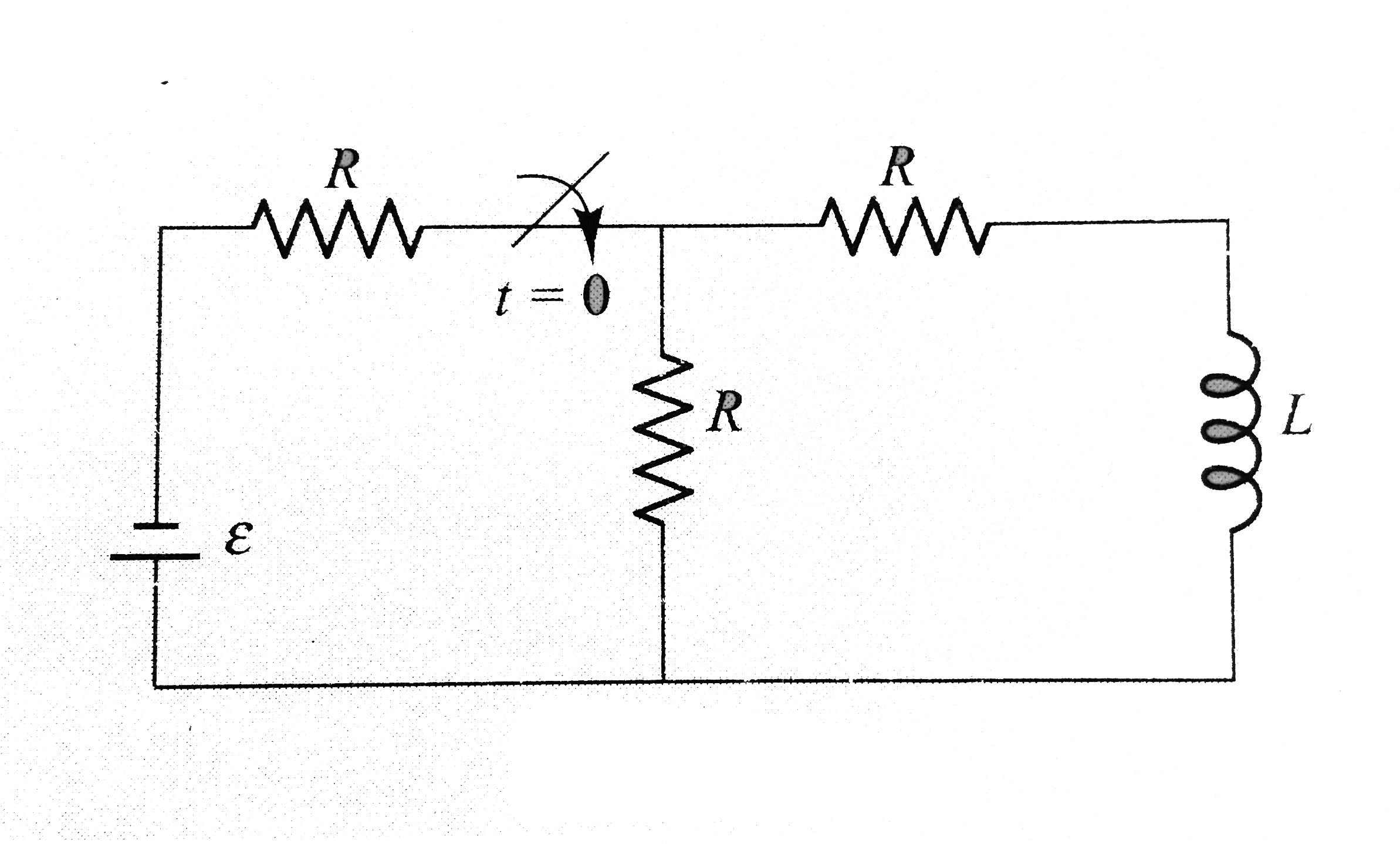
View Solution