If a particle moving along a line follows the law t=as2+bs+c, then the retardation of the particle is proportional to
square of the velocity
cube of the displacement
cube of the velocity
square of the displacement
The correct Answer is:C
To solve the problem, we need to analyze the given equation t=as2+bs+c and find the relationship between the retardation of the particle and its velocity. Here’s a step-by-step solution:
Step 1: Differentiate the equation with respect to time t
We start with the equation:
t=as2+bs+c
Differentiating both sides with respect to t:
dtdt=ddt(as2+bs+c)
This simplifies to:
1=2asdsdt+bdsdt
Step 2: Factor out dsdt
We can factor dsdt from the right-hand side:
1=(2as+b)dsdt
Rearranging gives us:
dsdt=12as+b
Step 3: Differentiate again to find acceleration
Now we need to find the acceleration d2sdt2. We differentiate dsdt again with respect to t:
d2sdt2=ddt(12as+b)
Using the quotient rule:
d2sdt2=−(2adsdt)⋅1(2as+b)2
Step 4: Substitute dsdt
Substituting dsdt=12as+b into the acceleration equation:
d2sdt2=−2a⋅12as+b(2as+b)2
This simplifies to:
d2sdt2=−2a(2as+b)3
Step 5: Relate acceleration to velocity
Recall that dsdt is the velocity v:
v=12as+b
Thus, we can express 2as+b in terms of v:
2as+b=1v
Substituting this back into the acceleration equation:
d2sdt2=−2av3
Conclusion
The retardation (negative acceleration) is proportional to the cube of the velocity:
Retardation∝v3
Thus, the retardation of the particle is proportional to the cube of its velocity.
t=as2+bs+c
dtdt=ddt(as2+bs+c)
1=2asdsdt+bdsdt
1=(2as+b)dsdt
dsdt=12as+b
d2sdt2=ddt(12as+b)
d2sdt2=−(2adsdt)⋅1(2as+b)2
d2sdt2=−2a⋅12as+b(2as+b)2
d2sdt2=−2a(2as+b)3
v=12as+b
2as+b=1v
d2sdt2=−2av3
Retardation∝v3
Topper's Solved these Questions
- DERIVATIVE AS A RATE MEASURER Book:OBJECTIVE RD SHARMA ENGLISHChapter:DERIVATIVE AS A RATE MEASURER Exercise:Section I - Solved Mcqs
Explore 27 Videos
- DEFINITE INTEGRALSBook:OBJECTIVE RD SHARMA ENGLISHChapter:DEFINITE INTEGRALSExercise:Chapter Test 2
Explore 56 Videos
- DIFFERENTIAL EQUATIONSBook:OBJECTIVE RD SHARMA ENGLISHChapter:DIFFERENTIAL EQUATIONSExercise:Chapter Test
Explore 30 Videos
Similar Questions
A particle moves according to the equation t=ax2+bx, then the retardation of the particle when x=ba is
View SolutionIf a particle is moving along straight line with increasing speed, then
View SolutionIf the velocity of a particle moving along x-axis is given as v=(3t2−2t) and t=0, x=0 then calculate position of the particle at t=2sec.
View SolutionThe x-t graph of a particle moving along a straight line is shown in figure
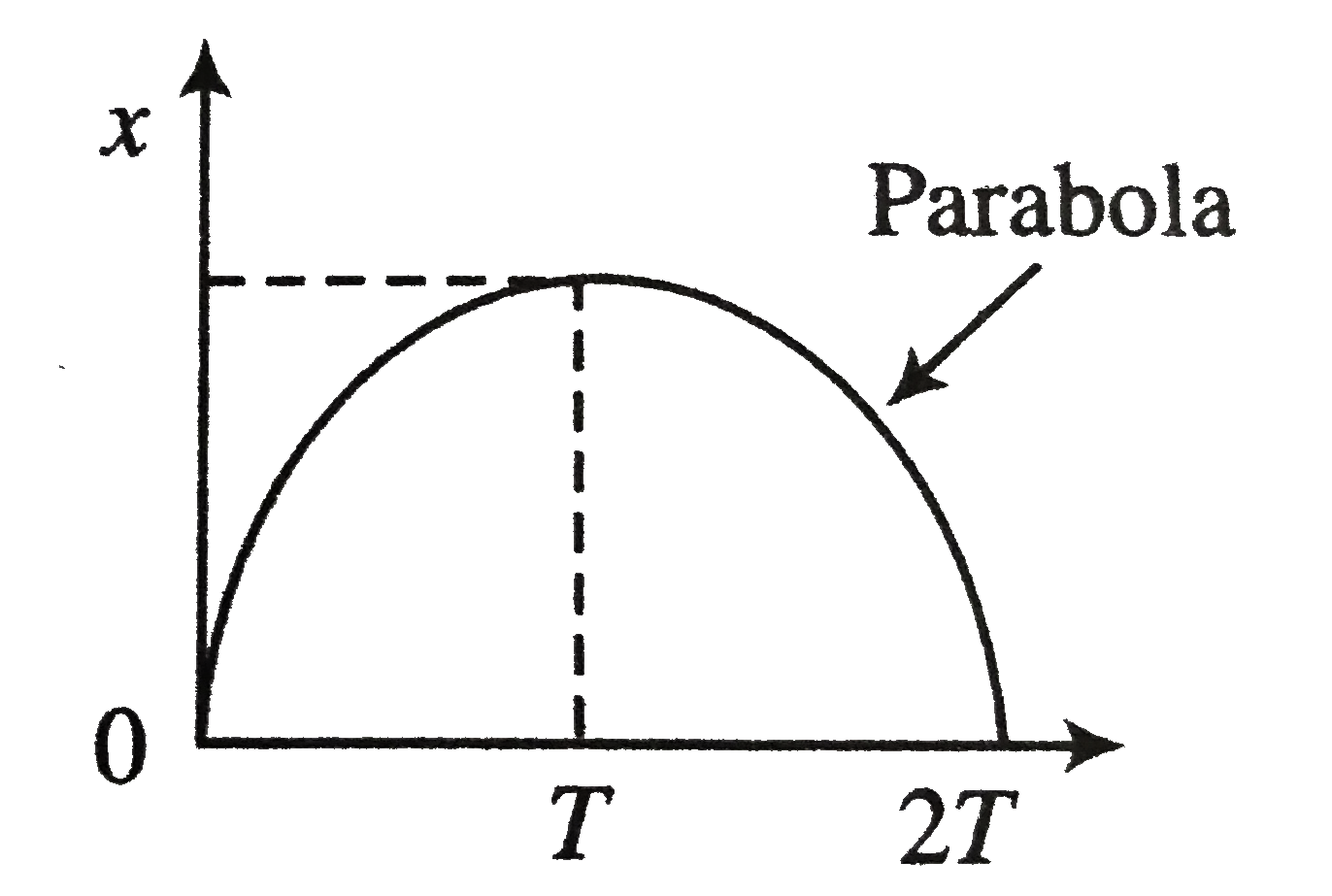
The a-t graph of the particle is correctly shown by
View SolutionThe x-t graph of a particle moving along a straight line is shown in figure
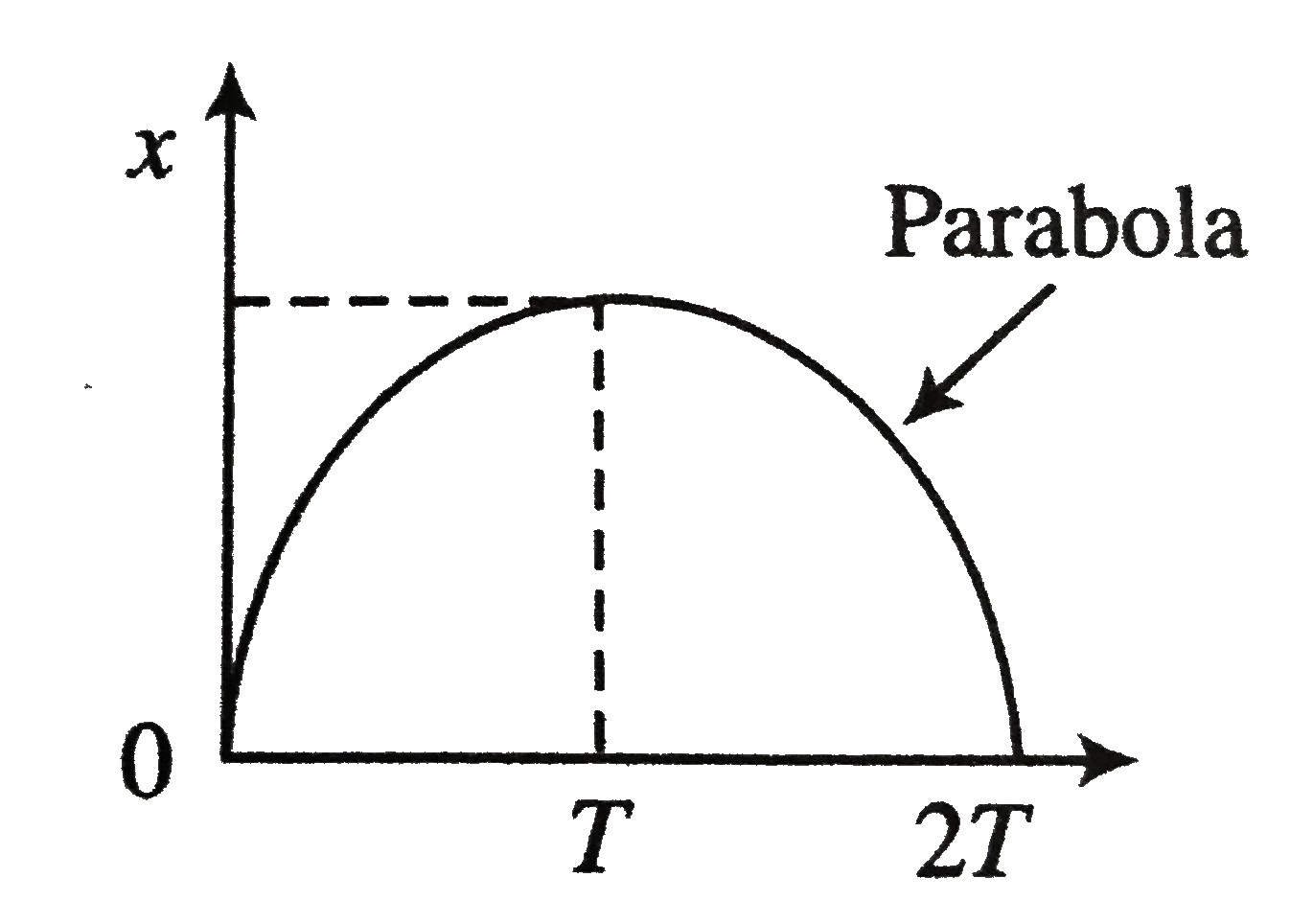
The v-t graph of the particle is correctly shown by
View SolutionThe distance traversed by a particle moving along a straight lne is given by x=180t+50t2 metre. The acceleration of the particle is
View SolutionThe x-t graph of a particle moving along a straight line is shown in figure

The speed-time graph of the particle is correctly shown by
View SolutionA particle move a distance x in time t according to equation x=(t+5)−1. The acceleration of particle is proportional to.
View SolutionA particle starts with speed v0 from x = 0 along x - axis with retardation proportional to the square of its displacement. Work done by the force acting on the particle is proportional to
View SolutionThe position of a particle moving along x-axis varies eith time t as x=4t−t2+1. Find the time interval(s) during which the particle is moving along positive x-direction.
View Solution