From the matrix equation AB=AC, we conclude B=C provided.
A is singular
A is non-singular
A is symmetric
A is square
The correct Answer is:B
Step by step video & image solution for From the matrix equation AB=AC, we conclude B=C provided. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DETERMINANTSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DETERMINANTSEXERCISE - Chapter Test
30 Videos
- DETERMINANTSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DETERMINANTSEXERCISE - Section II - Assertion Reason Type
6 Videos
- CARTESIAN CO-ORDINATE SYSTEM BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CARTESIAN CO-ORDINATE SYSTEM EXERCISE - Exercise
27 Videos
- DISCRETE PROBABILITY DISTRIBUTIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DISCRETE PROBABILITY DISTRIBUTIONSEXERCISE - Exercise
40 Videos
Similar Questions
Knowledge Check
From the passage, we can conclude that:
ANew ventures are not risky.BNew ventures are inherently risky.CFinancial investment in a new venture is always non-profitable.DConservative projection of companies' profits is suggestedIf the order of the matrix A is m×n and the order of the matrix B is n×p, then the order of matrix A.B is:
Am×nBn×pCm×pDp×p
If A, B, and C are three square matrices of the same order, then AB=AC⇒B=C. Then
View SolutionIf A∩B=A∪B then what can we conclude ?
View SolutionIn a parallelogram as shown in the figure (a≠b)
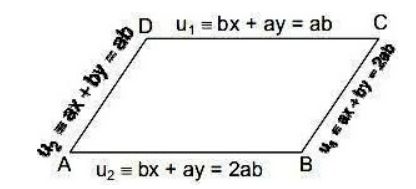
Prove that the equation of the diagonal AC is (a+b)x+(a+b)y=3ab
View SolutionIn a △ABC , B=(2,3),C=(7,-1) and AB=3,AC=5 then find the equation of altitude through the vertex A.
View SolutionLet A be an orthogonal matrix, and B is a matrix such that AB=BA, then show that ABT=BTA.
View SolutionIf A is matrix of order m×n and B is a matrix such that AB' and B'A are both defined , then order of matrix B is
View Solution

_E01_054_Q01.png)