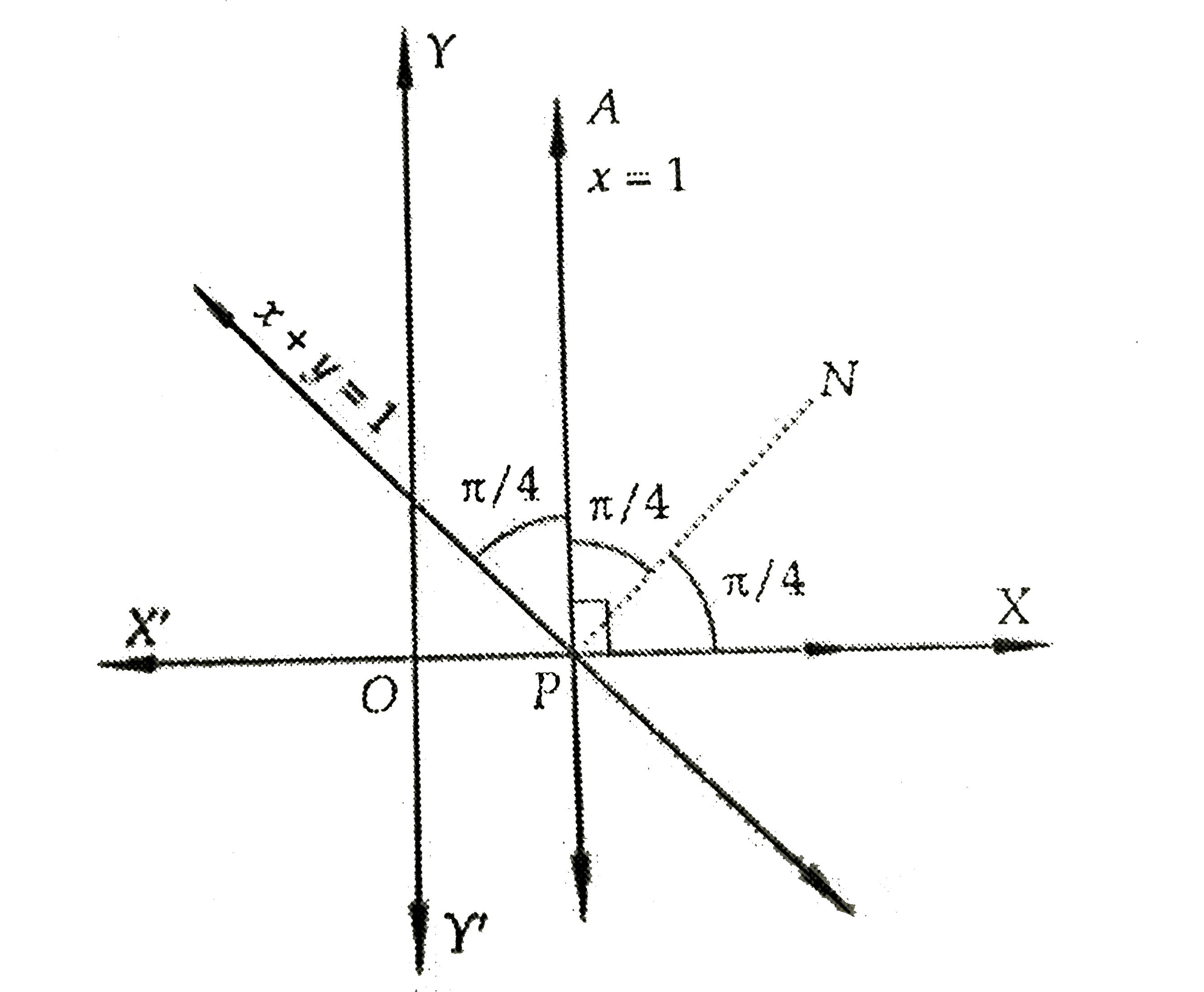
If a ray travelling along the line x=1 gets reflected from the line x + y = 1, then the eqaution the line along which the reflected ray travels is
y = 0
x - y = 1
x = 0
none of these
Clearly , the incidence ray makes 45∘ angle with the normal at P . So , the reflected ray will also make the same angle with the normal . Consequently , it is along x-axis i.e. y = 0 .
Topper's Solved these Questions
- STRAIGHT LINESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Section-1 Solved MCQs (Example)
1 Videos
- STRAIGHT LINESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - SECTION - II (ASSERTION - REASON TYPE MCQs)
14 Videos
- STRAIGHT LINESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - ILLUSTRATION 18
1 Videos
- SETSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SETSEXERCISE - Chapter Test
30 Videos
Similar Questions
If a ray travelling the line x = 1 gets reflected the line x+y=1 then the equation of the line along which the reflected ray travels is
View SolutionA ray of light travels along a line y=4 and strikes the surface of curves y2=4(x+y). Then the equations of the line along which of reflected ray travels is x=0 (b) x=2 (c) x+y (d) 2x+y=4
View SolutionCanal rays travel in a straight line.
View SolutionA ray of light is sent along the line 2x−3y=5. After refracting across the line x+y=1 it enters the opposite side after torning by 150 away from the line x+y=1 . Find the equation of the line along which the refracted ray travels.
View SolutionA ray of light travelling along the line OA (O being origin ) is reflected by the line mirror x−y+1=0 is the point of incidence being A (1,2) the reflected ray , travelling along AB is again reflected by the line mirror x−y=2, the point of incidence being B. If this reflected ray moves along BC, find the equation of the lne BC.
View SolutionA ray of light incident at the point (-2, -1) gets reflected from the tangent at (0, -1) to the circle x2+y2=1. The reflected ray touches the circle. The equation of the line along which the incident ray moved is
View SolutionA ray of light is sent along the line x−2y−3=0 upon reaching the line 3x−2y−5=0, the ray is reflected from it. Find the equation of the line containing the reflected ray.
View SolutionA ray of light is sent along the line x−2y−3=0 upon reaching the line 3x−2y−5=0, the ray is reflected from it. Find the equation of the line containing the reflected ray.
View SolutionA ray of light is sent along the line x−2y−3=0 upon reaching the line 3x−2y−5=0, the ray is reflected from it. Find the equation of the line containing the reflected ray.
View SolutionA ray of light travelling along the line x+y=1 is incident on the X - axis and after refraction the other side of the X - axis by turning π/6 by turning away from the X - axis .The equation of the line along which the refracted ray travels is
View Solution
