If the lengths of the sides of a triangle are in A.P. and the greatest angle is double the smallest, then a ratio of lengths of the sides of this triangle is:
3:4:5
4:5:6
5:6:7
7:8:9
The correct Answer is:B
Let the sides of the triangle be a-d,a and a+d, with a>d>0. Clearly, a-d is the smallest and a+d is the largest side. So, A is the smallest angle and C is the largest angle. It is given that C=2A. Thus, the angles of the triangle are A,2A and π−3A.
Applying the law of sines, we obtain
a−dsinA=asin(π−3A)=a+dsin2A
⇒ a−dsinA=asin3A=a+dsin2A
⇒ a−dsinA=a3sinA−4sin3A=a+d2sinAcosA
⇒ a−d1=a3−4sin2A=a+d2cosA
⇒ 3−4sin2A=aa−dand2cosA=a+da−d
⇒ 4cos2A−1=aa−dand2cosA=a+da−d
⇒ (a+da−d)2−1=aa−d⇒a=5d.
Thus, the sides of the triangle are
a-d,a,a+d i.e. 4d,5d,6d.
Hence, the ratio of the sides of the triangle is
4d:5d:6d i.e. 4:5:6.
Topper's Solved these Questions
- SEQUENCES AND SERIESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Section II - Assertion Reason Type
13 Videos
- SEQUENCES AND SERIESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise
129 Videos
- SEQUENCES AND SERIESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Chapter Test
59 Videos
- QUADRATIC EXPRESSIONS AND EQUATIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - QUADRATIC EXPRESSIONS AND EQUATIONS EXERCISE - Chapter Test
50 Videos
- SETSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SETSEXERCISE - Chapter Test
30 Videos
Similar Questions
The sides of triangle are in A.P. and the greatest angle exceeds the least by 90∘. The sides are in the ratio:
View SolutionIf the lengths of the sides of a triangle are in AP and the greatest angle is double the smallest, then a ratio of lengths of the sides of this triangle is
View SolutionThe angles of a triangle are in A.P. If the greatest angle is double the least, find the angles.
View SolutionIf the sides of a triangle are in A.P. and the greatest angle of the triangle exceeds the least by 90∘, then sine of the third angle is
View SolutionIf the lengths of the sides of a triangle are 3,5,7, then its largest angle of the triangle is
View SolutionIf the length of sides of right angled triangle are in AP, then their ratio is
View SolutionThe angles of a triangle are in A.P. The greatest angle is twice the least. Find all the angles
View SolutionThe lengths of the sides of a triangle are in the ratio 2:3:4. If the perimeter of the triangle is 63 cm, find the lengths of the sides of the triangle.
View SolutionFind the length of the third side of the triangle.
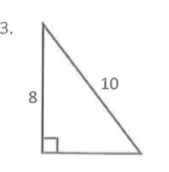
View SolutionFind the length of the third side of the triangle.
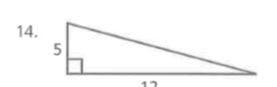
View Solution
