Question

If $b>a$, then the equation $(x-a)(x-b)-1=0$ has
(a) Both roots in $(a,b)$ (b) Both roots in $(-\infty ,a)$
(c) Both roots in $(b,+\infty )$ (d) One root in $(-\infty ,a)$ and the other in $(b,+\infty )$

Options

A. both roots in [a, b]
B. both roots in `(-oo, a]`
C. both roots in `(b, oo)`
D. one roots in `(-oo, a)` and other in `(b, oo)`

Answer

D

Explanation

Let `f(x) = (x - a)(x - b) -1`.
We observe that the coefficient of `x^(2)` in f(x) is positive and `f(a) = f(b) = - 1`. Thus, the graph of f(x) is as shown in Fig 18.

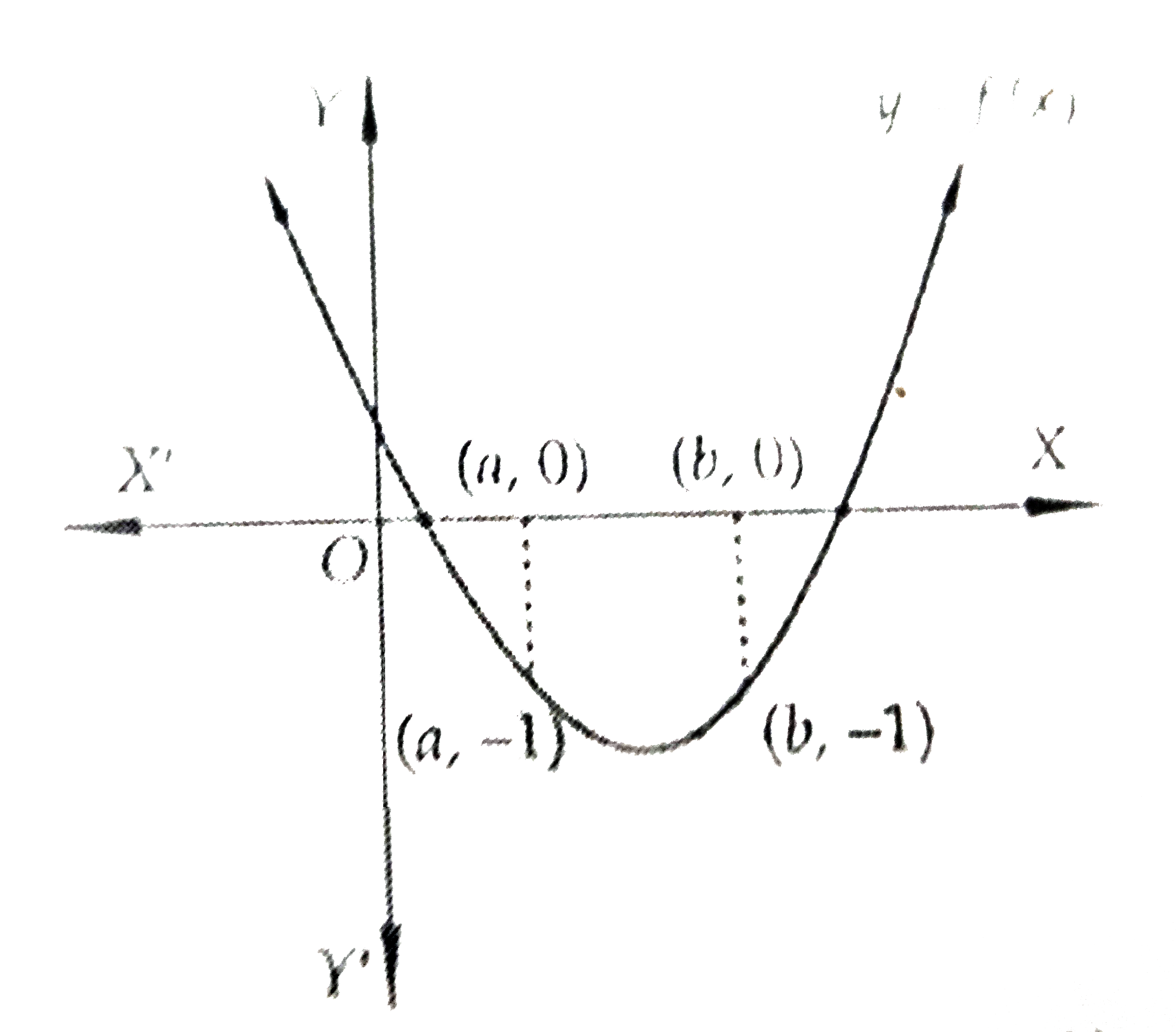
It is evident from the graph that one of the roots of f(x) = 0 lies in `(-oo, a)` and the other lies in `(b, oo)`.
Hence, option (d) is correct.